Функции APPEND и CONS конструируют списки

Если функции CAR и CDR разделяют списки на части, то APPEND и CONS их объединяют. Функция APPEND выстраивает в одну цепочку элементы всех списков, поставляемых в качестве аргументов:

 (APPEND '(АВ) '(С D)) 
   (А В С D) 

Обратите внимание на необходимость кавычек, не позволяющих рассматривать А и С в виде функций, действующих на свои аргументы. Необходимо понимать, что APPEND объединяет элементы списков, расположенные лишь на самом верхнем уровне:

APPEND '((А) (В)) '((С) (D))) 
дает 
 ((А) (В) (С) (D)) 
а не 
 (А В С D) 

Функция CONS в некотором смысле является дополнительной к CAR. Вместо отщепления от списка первого элемента эта функция берет список и вставляет в него новый первый элемент. Договоримся слова между угловыми скобками воспринимать как описание того, что должно стоять в указанной позиции. Тогда функция CONS может быть описана следующим образом:

(CONS <новый первый элемент> <некоторый список>)

Таким образом, мы имеем

(CONS 'А '(В С)) 
 (ABC) 

Если мы наберем на терминале (CONS '(А В) '(С D), то результатом будет ((А В) С D), где список (А В) стал первым элементом списка, который раньше имел вид (С D).

Обратите внимание на различие функций CONS и APPEND

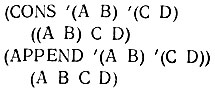
Атомы имеют значения

До сих пор мы рассматривали, каким образом символьные структуры разделяются на части и объединяются путем операций над списками, начинающимися с CAR, CDR, APPEND и CONS. Мы видели также, как осуществляется арифметика путем вычисления списков, начинающихся с PLUS, DIFFERENCE и других подобных функций. В самом деле, похоже, что целью системы Лисп всегда является что-то вычислить и вернуть значение. Это верно как для списков, так и для атомов. Предположим, мы набрали на терминале простой атом X и ждем от системы ответа. Получив X, Лисп пытается вернуть значение точно так же, как если бы мы набрали некоторое выражение типа (PLUS 3 4). Но значение атома должно быть найдено из таблицы, а не в результате вычисления, как при работе со списками.

Вообразим таблицу, в которой в одном направлении располагаются имена атомов, а в другом - названия свойств. См. рис. 11.1. Величина, или значение, атома - это просто одно из свойств, которым может обладать атом. Это свойство несколько специализировано в том смысле, что оно представляет собой результат, который получается, когда оценивают атом.

• Т и NIL являются особыми атомами в том отношении, что их значения заранее положены равными Т и NIL, т. е. значение Т всегда есть Т, значение атома NIL всегда есть NIL.
• Все числа также обладают этим свойством. Значение числа всегда равно этому числу.

Многие другие названия и значения свойств пользователь может придумать сам. Примером является свойство ОТЕЦ. Из таблицы видно, что значением свойства ОТЕЦ для атома LEIF является ERIK. Заметим, что значением свойства может служить любое s- выражение. Свойством РОДИТЕЛИ для человека по имени LEIF мог бы быть список из двух элементов, указывающий имена его родителей. Функции для приписывания значений свойствам и извлечения этих значений будут описаны позднее. Сейчас же достаточно усвоить, что свойство значения для атома представляет собой лишь частный случай более общего понятия.

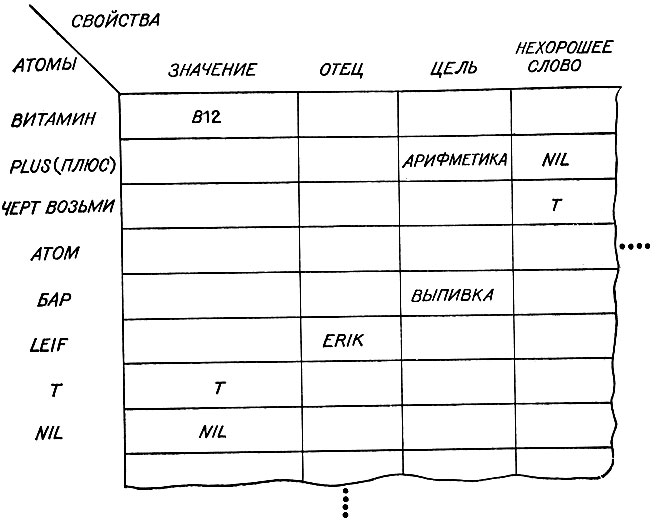
Рис. 11.1. Атомы и их свойства образуют таблицу свойств. В данном примере ERIK является значением свойства ОТЕЦ для атома LEIF. Свойство ЗНАЧЕНИЕ является лишь одним из свойств

Заметим, кстати, что слово значение (value) используется нами в двух смыслах: во-первых, мы говорим о значении некоторого конкретного свойства некоторого конкретного атома, а во-вторых, мы говорим о некотором специальном свойстве, имя которому - значение. Таким образом, можно всерьез говорить о значении свойства значения, хотя обычно говорят в этом случае только о значении.

В частном случае свойства значения само значение устанавливается специальной функцией SET. Она приводит к тому, что значение ее второго аргумента становится свойством значения ее первого аргумента. Набор на терминале выражения (SET 'L'(A В)) задает (А В) в качестве значения для этого выражения. Но, что важнее, здесь имеется побочный эффект, потому что (А В) присваивается L в качестве значения свойства "значение". Если мы теперь наберем L, то в ответ получим (А В).

Таким образом, выражение (SET (арг 1) (арг 2)) применяется главным образом из-за этого побочного эффекта присваивания значения атому (арг 1).

Теперь, поскольку значение L установлено равным (А В), то L можно использовать в примерах, демонстрирующих работу основных функций оперирования со списками. Примеры иллюстрируют то обстоятельство, что Лисп ищет значения атомов не только в тех случаях, когда они появляются сами по себе, но и тогда, когда атомы служат аргументами функций. Сообщения об ошибках (ERROR), появляющиеся ниже, объясняются тем, что функция получает на свой вход атом, когда ей необходим список.

Заметим, что функция EVAL (сокращение от слова оценивать - evaluate) явным образом вызывает следующую последовательность действий. Сначала происходит вычисление значения атома А, поскольку это идущий без кавычек аргумент функции. Затем отыскивается значение результата, поскольку таков смысл функции EVAL. Функция EVAL всегда выдает значение своего аргумента.

Предикат - это функция,

значение которой равно либо Т, либо NIL

Наша следующая задача - понять работу некоторой совокупности функций, называемых предикатами. Предикат представляет собой функцию, значение которой ограничено двумя специальными атомами, Т или NIL. Эти значения Т и NIL соответствуют разговорному представлению понятий "истина" и "ложь".

Предикат NOT (НЕТ) возвращает Т, только если его аргументом является NIL. NULL (НУЛЬ или ПУСТО) проверяет, не является ли аргумент пустым списком.

Предикат MEMBER (ВХОДИТ) возвращает T, только если его первый аргумент является элементом последующего списка. При этом недостаточно, чтобы этот первый аргумент был где-то похоронен во втором аргументе: требуется, чтобы это был элемент верхнего уровня списка.

Для наших дальнейших примеров давайте установим значение X точно так же, как и значение L. Удобно ввести функцию SETQ, которая подобна SET, но в ней не делается попытки найти значение первого аргумента. Благодаря этому SETQ становится как бы идиомой, поскольку в общем случае значения всех аргументов должны быть найдены прежде, чем функция начинает свою работу. Функция SETQ намного популярнее, чем SET.

Часто применения SETQ следуют одно за другим. Тогда аргументы, нечетные по порядку, не оцениваются, а оцениваются аргументы четные, как и следовало бы ожидать. Таким образом, одна функция SETQ может выполнить ту работу, которая была выполнена двумя функциями в примере выше:

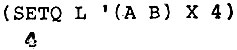
Теперь, используя значения, установленные для X и для L, имеем следующее^*:

^* (NUMBERP - является числом, GREATERP - больше, LESSP - меньше, ZEROP - равен нулю, EQUAL - равны.- Прим. перев. )

Обратите внимание, что несколько предикатов оканчивается на букву Р, мнемоника, используемая для предиката (predi cate). Предикат АТОМ является неудачным исключением, которое наводит на мысль, что и LIST (СПИСОК) является предикатом. Но это не так. LIST представляет собой функцию, аргументы которой заключаются в круглые скобки, при этом создается новый список, вложенный на один уровень круглых скобок глубже любого ее аргумента:

Предикаты помогают функции COND произвести выбор между различными альтернативами

Предикаты наиболее часто используются для определения, по какому из возможных путей должна развиваться программа. В действительности путь, или ветвь, часто определяется предикатами вместе с функцией ветвления COND, поэтому COND является наиболее употребимой функцией. К сожалению, у нее несколько специфический синтаксис. За функцией, называемой COND, идет некоторое число списков, каждый из которых содержит проверку и нечто, чье значение следует выдать, если условие в проверке оказывается выполненным. Таким образом, в общем случае указанный синтаксис выражается так:

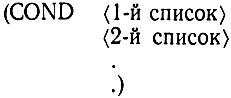
Каждый список называется предложением. При более подробном описании предложений мы получаем

Значение какого-то одного из результирующих элементов и будет значением всей функции COND. Идея состоит в том, чтобы проходить по спискам, обращая внимание только на их первые элементы, до тех пор, пока не найдется элемент, значение которого не равно NIL. Тогда все остальное в этом отобранном списке подвергается оцениванию, и значение последней из оцениваемых величин выдается в качестве значения функции COND. Ясно, что любые выражения, стоящие между первым и последним элементами в списке функции COND, должны использоваться только из-за побочных эффектов, поскольку никоим образом они не могут повлиять на значение COND.

Имеется два частных случая:

• Если ни один подходящий список не найден, COND возвращает NIL.
• Если выбранный список содержит ровно один элемент, то возвращается значение этого элемента. Иными словами, (тест) и (результат) могут совпадать.

Кстати, может показаться странным, что для выбора между предложениями не требуется строгого Т, а годится все, что отлично от NIL. Такое свойство желательно потому, что оно позволяет в качестве тестовых функций использовать не только функции, значения которых, как в случае предикатов, ограничены двумя величинами - Т и NIL. Много таких примеров будет дано в дальнейшем.

Если говорить о странных вещах, то одной из них стоит уделить специальное внимание:

• Пустой список ( ) и NIL эквивалентны во всех отношениях. Например, они удовлетворяют предикату равенства, т. е. (EQUAL NIL'( )) возвращает Т.

Одни говорят, что так первоначально было сделано в связи со спецификой системы машинных команд очень старой вычислительной машины 709. Другие уверены в том, что такое тождество всегда считалось удобным с программистской точки зрения. Никто точно причины не знает. Во всяком случае, первым элементом в предложении COND часто оказывается переменная, значением которой служит некоторый список, и этот список может оказаться пустым. Если этот список пуст, то данное предложение в COND не срабатывает, поскольку значение пустого списка равно NIL. С другой стороны, часто встречаются ошибки, вытекающие из того факта, что (АТОМ'()) есть Т.