Программирование на языке Лисп
Теперь мы располагаем ингредиентами. Посмотрим, как из них можно комбинировать новые функции, используя функцию DEFINE (ОПРЕДЕЛЕНИЕ). Она имеет следующий синтаксис:
(DEFINE (форма) (описание процесса))
Как и прежде, в угловых скобках размещаются описания различных объектов. (Эти описания могут относиться к атомам, спискам и даже отдельным фрагментам, если это необходимо.) Функция DEFINE не требует значения своих аргументов. Она просто обращается к ним и устанавливает некоторое функциональное соответствие в качестве своего побочного эффекта. Возвращаемой величиной при этом является имя функции, что для дальнейшего не существенно.
DEFINE образует новые функции
Вместе с DEFINE используется очень простая функция POWER (СТЕПЕНЬ), работающая со степенями 0,1 и 2, она строится следующим образом:

Когда такое определение сделано, функцией POWER очень удобно пользоваться:

Обратите внимание: та часть определения, которая обозначена нами (форма), задает внешний вид функции, которая будет применяться. Она дает имя функции и указывает на число используемых аргументов. Важно и то, что она показывает также, как эти аргументы используются функцией. Не указав где-нибудь в определении функции имена переменных в том порядке, в котором они передаются этой функции, невозможно было бы решить, означает ли (POWER) 3 2) 32 или 23, поскольку нет способа узнать, какое из соответствий

нам нужно.
То, что в действительности происходит, когда мы используем функцию POWER, выглядит как последовательность действий, показанных на рис. 11.2.
Переменные могут быть свободными или связанными
Этот процесс присваивания значений переменным при входе в функцию называется, как это исторически сложилось, LAMBDA-связыванием.
Чтобы проверить, усвоили ли вы основную идею, обратимся к следующей функции NONSENSE (БЕССМЫСЛИЦА). См. след. стр. Значение Y изменилось, а значение X - нет. Временно X было изменено - оно стало равным 9 при входе в функцию NONSENSE, а затем стало равным 3, благодаря действию SETQ. Различие состоит в том, что X было присвоено значение при входе и восстановлено старое значение при выходе, потому что оно появляется в части (форма) определения функции. Мы говорим, что X связана по отношению к функции NONSENSE, тогда как Y в том же контексте является свободной переменной. Бессмысленно говорить о том, свободна или связана переменная, если при этом не задано, по отношению к какой функции она свободна или связана.
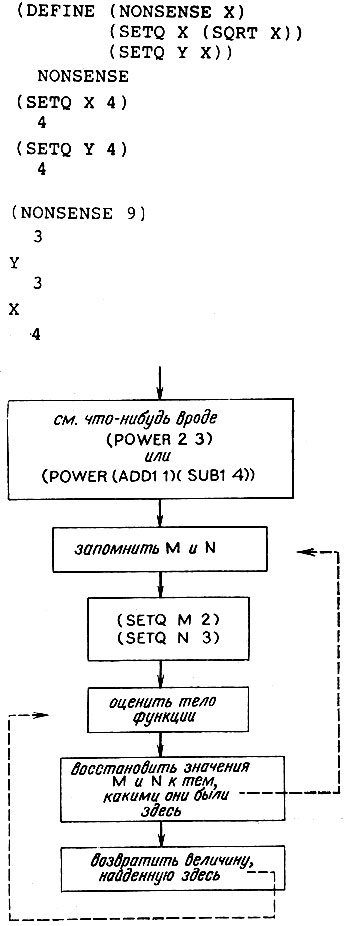
Рис. 11.2. При входе в функцию переменные, указанные в части определения функции, названной 'форма', получают значения, которые используются при оценивании тела функции. Значения переменных восстанавливаются при выходе из функции
Рекурсия позволяет функциям использовать самих себя
Теперь мы готовы проследить историю переменных в более сложных ситуациях, когда для одной переменной может храниться много значений. Эти ситуации встречаются тогда, когда некоторая функция решает задачу циклически, слегка упрощая ее на каждом этапе и начиная все сначала, отправляясь уже от упрощенной формы. Например, для того чтобы вычислить N-ю степень некоторого числа М, достаточно выполнить задачу для степени N-1, поскольку этот результат, помноженный на М, и является искомым результатом для N-й степени. Определения, в которых описывается периодически повторяющийся процесс решения одной и той же задачи заново с более простыми аргументами, называются рекурсивными. Обратимся к рекурсивной функции POWER (СТЕПЕНЬ), выраженной на языке Лисп:

Глядя на рис. 11,3 мы можем легко проследить историю М и N, по мере того как Лисп вычисляет (POWER 2 3). Чтобы показать работу рекурсии, используется дерево, где ветви под узлом представляют новые обращения к функции, как это требуется в ходе вычисления, проводящегося в этом родительском узле. Каждое обращение перечисляется в соответствии с его порядком в последовательности обращений к функции. Идущие вниз линии показывают аргумент или аргументы, переносимые вниз, тогда как идущие вверх линии указывают возвращаемые величины.
Рассмотрев рекурсию в действии для простой численной задачи, посмотрим на рекурсивную функцию COUNTATOMS (ПОДСЧЕТ АТОМОВ), которая подсчитывает отличные от NIL атомы в данном s-выражении:
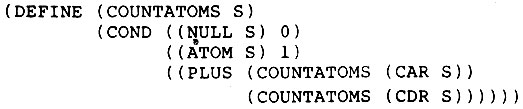
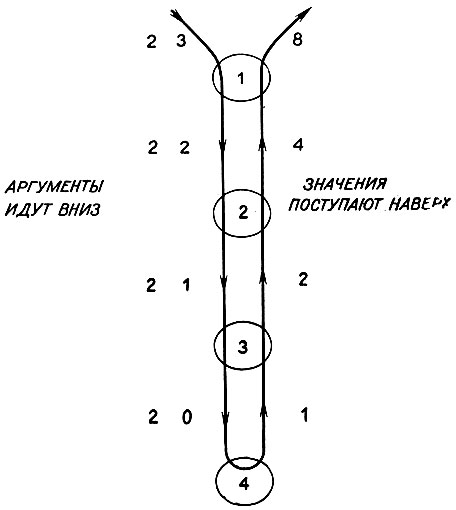
Рис. 11.3. Моделирование часто помогает разобраться в стратегии рекурсивной программы. Здесь каждая копия функции POWER (СТЕПЕНЬ) уменьшает N на единицу и передаёт его дальше, пока оно не станет равным нулю. Стрелочки показывают переход управления от одного из перечисленных применений функции к другому. Аргументы показаны у направленных вниз стрелочек, а возвращаемые величины - у стрелочек, направленных вверх
В первой строке указано, что определяется функция COUNTATOMS одного аргумента S. Первые два предложения функции COND перечисляют самые простейшие случаи, когда возвращается 0 для пустых списков и 1 для атомов. В третьем предложении обрабатываются другие ситуации, посредством преобразования сложных задач в простые. Списки разбиваются на части с использованием CAR и CDR, и затем функция COUNTATOMS применяется к обоим получившимся фрагментам. Поскольку каждый атом в списке попадает либо в CAR, либо в CDR, то каждый атом оказывается учтенным. Функция PLUS объединяет результаты. В конечном счете, возможно, после многих и многих применений самой себя функция COUNTATOMS сводит трудные случаи либо к первому, либо ко второму предложению, которые обрабатываются функцией COND.
Здесь полезно рассмотреть, как COUNTATOMS разбирает s-выражения на части и сводит их последовательно к более простым случаям. Как показано на рис. 11.4, конкретное выражение, число атомов которого необходимо подсчитать,- это (TIMES X (SQRT 4)). Обратите внимание, что это выражение для данных само по себе имеет форму выражения, которое, как можно подумать, могло бы использоваться для нахождения некоторого значения. Здесь мы имеем пример фрагмента программы, COUNTATOMS, исследующего некоторый другой фрагмент программы и выполняющего над ним определенные вычисления.
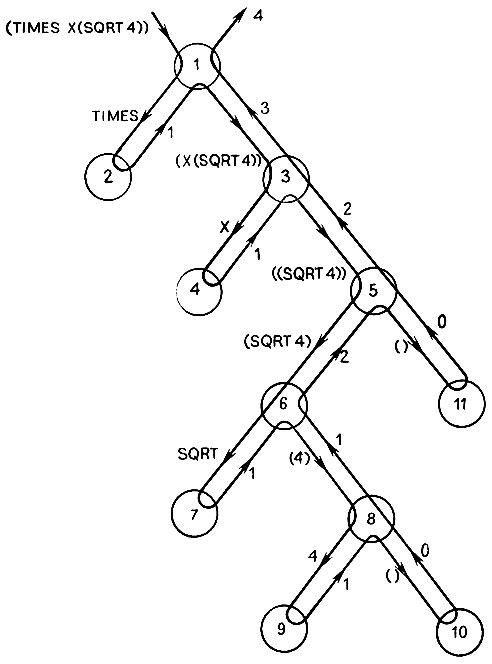
Рис. 11.4. Снова моделирование помогает понять стратегию рекурсивной программы. Здесь s-выражение (TIMES X (SQRT 4)) разбивается на составляющие его компоненты с помощью функции COUNTATOMS. Стрелочки показывают передачу управления от одного из перечисленных применений функции к другому. Аргументы показаны у стрелочек, направленных вниз, возвращаемые величины - у стрелочек, направленных вверх
На каждом шаге аргумент для функции COUNTATOMS подразбивается на две меньшие части. Когда будут получены результаты для каждой из этих частей, они будут просуммированы функцией PLUS, которая вернет значение на более высокий уровень дерева.
Заметим что, Т, стоящее в COUNTATOMS, гарантирует, что последнее предложение сработает обязательно, если не сработают все остальные предложения в COND. Т часто можно встретить в последнем предложении функции COND, где оно очевидным образом устанавливает, что процесс должен остановиться. Хотя на самом деле Т не является необходимым, так как тот же самый результат получится и без него:
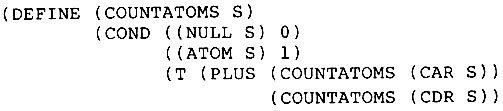
Это выражение работает потому, что COND срабатывает на чем угодно, отличном от NIL, а не только на Т. Функция PLUS никогда не может дать NIL, и поэтому предложение заведомо срабатывает точно так же, как если бы Т там присутствовало. Поскольку здесь в последнем предложении имеется ровно один элемент, то этот элемент является и первым, и последним и обеспечивает как необходимый тест, так и создание возвращаемого значения.
Хорошая программистская практика говорит за использование Т, потому что присутствие Т явно свидетельствует о том, что должно сработать последнее предложение, если все остальные не срабатывают. Использование Т говорит явно о том, что никогда не произойдет "выпадения" из функции COND, что дало бы по умолчанию значение NIL.
Для работы со списками аргументов часто привлекаются МАРСАR и APPLY
Несколько более элегантный путь определения программ, подобных COUNTATOMS, состоит в использовании функций MAPCAR и APPLY, двух новых функций, которые весьма полезны и весьма специфичны в отношении того, как они работают со своими аргументами.
MAPCAR используется тогда, когда одна и та же операция должна быть произведена на всем списке элементов. Предположим, например, что нужно прибавить 1 к каждому числу из некоторого списка чисел. Например, если мы из (1 2 3) хотим получить (2 3 4).
Чтобы выполнить такую операцию с помощью функции MAPCAR, необходимо задать имя операции вместе со списком тех элементов, которые должны один за другим подаваться на вход этой операции.
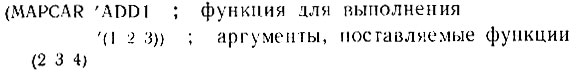
Не накладываются требования, чтобы функции были функциями одного аргумента, но если используемая функция является функцией более чем одного аргумента, то должно присутствовать соответствующее число списков, поставляемых этой функции. MAPCAR работает, как сборочная машина, выбирая один элемент из каждого списка аргументов и собирая их вместе для использования в функции:
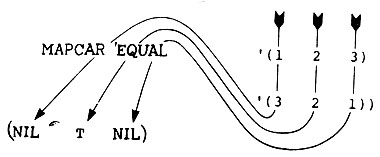
Рассмотрим теперь распространенную ошибку, которая показывает, почему необходима функция APPLY. Предположим, что мы хотим просуммировать некоторый список чисел L.
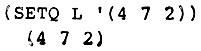
Хотим ли мы при этом вычислить (PLUS L)? Нет! Это неверно, поскольку на входе PLUS используются аргументы, представляющие собой числа. А здесь функции PLUS предъявлен один аргумент, представляющий собой список чисел. PLUS может только подавиться и закашлять, не зная, что делать с такой неожиданной для него формой аргумента. Это выглядело бы так же, как если бы мы пытались вычислить (PLUS '(4 7 2)) вместо (PLUS 4 7 2).
Чтобы заставить PLUS работать, мы должны использовать функцию APPLY, которая воспринимает два аргумента, имя функции и список и организует дело так, чтобы функция работала с элементами этого списка, как если бы они предъявлялись как нормальные ее аргументы. Таким образом.
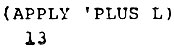
представляет собой частный случай более общий формы:
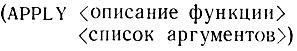
Теперь, используя функции APPLY и MAPCAR, мы можем построить более изящный метод подсчета атомов:

Глядя на первые два предложения функции COND, мы видим, что простые случаи обрабатываются, как и раньше. И снова целью является сведение более сложных выражений к более простым. Только теперь для упрощения s-выражений применяется не CAR и CDR, a MAPCAR. В этом варианте функции COUNTATOMS используется умение функции MAPCAR обратиться к каждому элементу списка с некоторой определенной функцией; в данном случае рекурсивно применяется сама функция COUNTATOMS.
Теперь, предполагая, что эта функция работает, мы видим, что MAPCAR возвращает список чисел, которые нужно сложить друге другом. Поэтому появляется функция APPLY. Функции PLUS нужны числа, а не список чисел. Функция APPLY служит соответствующим интерфейсом и поставляет список чисел функции PLUS так, как если бы каждый элемент списка сам по себе был аргументом для функции PLUS.
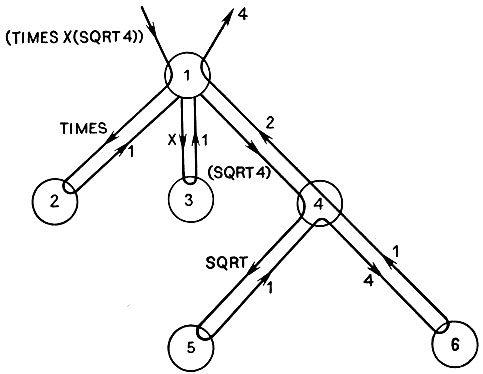
Рис. 11.5. Вариант COUNTATOMS (ПОДСЧЕТ АТОМОВ) с использованием функции MAPCAR вместо функций CAR и CDR демонстрирует меньшую глубину рекурсии. Здесь только шесть вхождений на трех уровнях вместо одиннадцати на шести, как это было раньше
Теперь легко можно модифицировать COUNTATOMS, чтобы делать другие вещи. Например, для того чтобы определить глубину
Смоделировать такую функцию COUNTATOMS легче, чем раньше, поскольку рекурсия менее сложна и менее глубока. См. рис. 11.5.
s-выражения, нужно внести в COUNTATOMS следующие изменения: заменить имя функции на DEPTH (ГЛУБИНА), изменить результаты в случае пустого списка и атома, заменить PLUS на МАХ и вставить ADD1. Эти изменения приводят к функции DEPTH:

На рис. 11.6 показано, как функция DEPTH работает над тем же самым выражением, которое раньше было использовано для иллюстрации работы функции COUNTATOMS. Снова в каждой точке ветвления мы видим, как MAPCAR расщепляет выражение на более простые элементы, над которыми выполняется дальнейшая обработка.
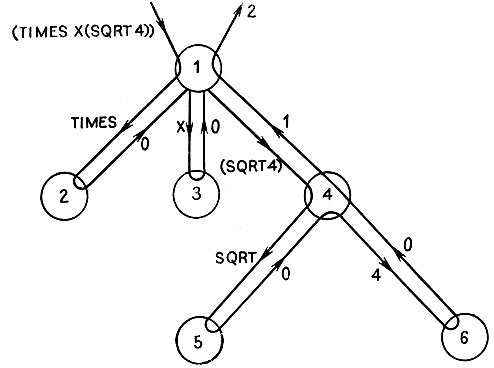
Рис. 11.6. Рекурсия для функции DEPTH (ГЛУБИНА) носит в точности тот же характер, что и рекурсия для функции COUNTATOMS
Локальные определения осуществляются с использованием LAMBDA
Чтобы ввести следующую функцию, рассмотрим задачу поиска таких элементов списка, которые представляют собой числа, заключенные между двумя границами, названными HIGH (ВЕРХНЯЯ) и LOW (НИЖНЯЯ). Одним из походов было бы определить функцию TEST, используя GREATERP, предикат, который воспринимает произвольное количество числовых аргументов и возвращает Т, если эти аргументы появляются в порядке их убывания:
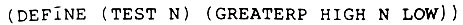
Тогда мы можем написать

Это несколько неудобно. При прохождении по некоторому списку с простой процедурой отвлекаться, чтобы определить функцию, кажется неестественным. Почему бы намерения программиста не сделать более прозрачными, описывая необходимую процедуру непосредственно в том месте, где она используется.
(MAPCAR (DEFINE (TEST N) (GREATERP HIGH N LOW)) L)
Функция DEFINE здесь работает потому, что функции MAPCAR требуется имя функции, а значение DEFINE является именем определяемой функции. Но чтобы избежать ненужного размножения имен, имя можно опустить, если оно используется только здесь. В нашем случае об отсутствии имени функции сообщается путем использования другого способа определения функции, несколько отличного от DEFINE. По историческим соображениям эта новая функция определения функции использует имя LAMBDA. Поэтому корректный путь образования локального определения будет таким:
(MAPCAR '(LAMBDA (N) (GREATERP HIGH N LOW)) L)
- В действительности никто не будет использовать DEFINE в функции MAPCAR, поскольку это было бы чрезвычайно неэффективно: все трудности, связанные с формированием некоторой функции и неизбежными затратами, возникали бы каждый раз при выполнении данного фрагмента программы. Функцию DEFINE мы применили здесь лишь для того, чтобы объяснить, для чего нужно LAMBDA-определение.
Более длинным именем, но, пожалуй, более информативным, для локально определяемых функций было бы DEFINE-ANONYMOUS (АНОНИМНОЕ ОПРЕДЕЛЕНИЕ). Но по причинам совместимости с прежними версиями Лиспа мы будем придерживаться LAMBDA. Для лучшего понимания хорошей эвристикой будет переводить LAMBDA, как DEFINE-ANONYMOUS.
Заметим, что в LAMBDA - определениях требуется кавычка, чтобы предотвратить оценивание. Таким образом, MAPCAR не получает имени функции, вместо этого для работы ей поставляется описание функции. Это не важно. Функция MAPCAR может работать как с именем функции, так и с ее описанием.
Функция LAMBDA иногда используется в качестве интерфейса (сопряжения) между функциями и списками аргументов. В следующем примере используется функция PRESENCE (ПРИСУТСТВИЕ), которая определяет, сколько раз данный атом X встречается в выражении S. (В системах символьной математики такая функция используется для определения, является ли некоторое s-выражение константным.)

Здесь функция LAMBDA нужна для приведения в соответствие функции PRESENCE, функции двух переменных, с единственным списком аргументов функции MAPCAR. Использование PRESENCE на месте LAMBDA-определения представляет собой распространенную ошибку. Поскольку в функции PRESENCE ожидается два аргумента и поскольку имеется всего лишь один список, S, поставляющий аргументы, то такая программа была бы обречена.
Интерпретатор помогает объяснить, как работает Лисп
Что же именно делает Лисп с выражением, которое набирается на терминале? Другими словами, как выглядит процесс нахождения значения выражения, если представить его в виде блок-схемы?
Блок-схема на рис. 11.7 показывает, что происходит на самом деле. Учтите, что она не обязательно соответствует тому, как это происходит на уровне реализации системы.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'