Реализация минимаксного поиска

Для начала совершенно ясно, что игровое дерево может быть непосредственно представлено в виде списковой структуры. Каждый узел представляется в виде списка, элементы которого - это узлы, идущие ниже. На рис. 13.1 изображено, как это можно сделать.

Основную минимаксную процедуру реализовать легко

Вспомним, как работает минимаксный метод. Применение минимаксных правил для определения наилучшего хода для игрока в верхней точке означает попеременный поиск максимума и минимума из оценок ситуаций при движении по дереву снизу вверх.

Легко написать функцию BIGGEST (НАИБОЛЬШИЙ), которая практически точно выполняет такую задачу:

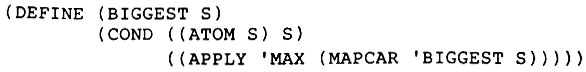
Если эта функция применяется к списковому представлению для игрового дерева, которое мы используем в нашем примере, то она заканчивает свою работу, возвращая наибольшее число в нашем s-выражении, а именно 9, поскольку на каждом уровне рекурсии возвращается наибольшее из предъявленных чисел.

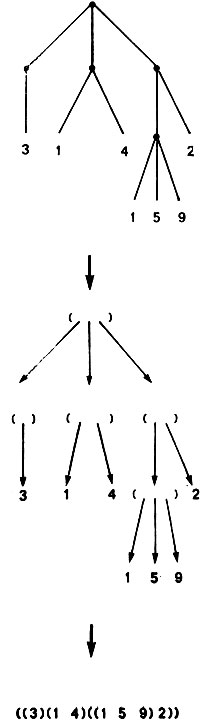
Рис. 13.1. Игровые деревья легко представляются в виде s-выражений.

Функция SMALLEST (НАИМЕНЬШИЙ), определяемая очевидным образом как дополнительная к функции BIGGEST, также делает не то, что требуется. Интересно, что эти две функции с небольшим изменением могут быть скомбинированы, чтобы получить то, что нам нужно:

Функции BIGGEST и SMALLEST должны были подвергнуться нескольким изменениям, пока не было достигнуто требуемое поведение. Эти изменения отражают то, что делает программист, отталкиваясь от этой простой базовой программы и приходя в конечном счете к процедуре отсечения по методу альфа-бета. BIGGEST1 и SMALLEST 1 являются первыми в такой последовательности. Как и в случае BIGGEST, функция BIGGEST 1 использует МАХ, чтобы получить наибольший элемент, возвращаемый функцией MAPCAR. Но теперь MAPCAR использует уже SMALLEST 1. Очевидно, что функция МАХ работает с результатами, получаемыми применением SMALLEST 1 к каждому элементу аргумента S функции BIGGEST 1. В свою очередь SMALLEST 1 использует MIN по результатам применения BIGGEST 1 к каждому элементу ее аргумента. Таким образом, мы достигаем необходимое чередование максимизации и минимизации на каждом уровне. Результат верхнего уровня представляет собой счет, который достигается в нижней части дерева вдоль такого пути, на котором каждый из участников в каждом узле дерева игры выбирает наилучший ход.

Можно связать генерирование ходов и минимаксную процедуру

Конечно, очень хорошо возвращать ожидаемый счет, используя полностью построенное дерево, но это дерево тоже должно как-то быть построено. Это можно было бы сделать, используя независимую программу, но лучше сразу предусмотреть использование в дальнейшем отсечения по методу альфа-бета и объединить минимаксную процедуру с генерацией ходов.

К счастью, нет необходимости вникать в детали того, как для данной игры могла бы быть построена статическая оценка и сгенерирован наиболее разумный ход. Вместо этого мы предположим, что существует функция STATIC-VALVE (СТАТИЧЕСКАЯ-ОЦЕНКА), которая в качестве аргумента воспринимает позицию в игре и возвращает свое мнение относительно силы позиции в виде одного числа. Далее мы предположим существование функции генератора ходов, PLAUSIBLE-MOVES (ДОПУСТИМЫЕ-ХОДЫ), которая воспринимает описание позиции и возвращает список новых позиций, достижимых за один ход. В общем случае этот список новых позиций может оказаться пустым, если PLAUSIBLE-MOVES найдет ситуацию безвыходной, но пока что мы предположим, что генератор допустимых ходов порождает по крайней мере одного кандидата.

Теперь дерево можно генерировать быстро. Аргумент передается функции BIGGEST2, как представление единичной позиции, а не дерева целиком. Эта единственная позиция исследуется внутри функции BIGGEST2 посредством PLAUSIBLE-MOVES. Заметьте, что рекурсия (и генерация ходов) заканчивается, когда функция QUIET (СПОКОЙСТВИЕ) решает, что ситуация на игровой доске достаточно успокоилась, чтобы построить хорошую статическую оценку.

Поскольку функция SMALLEST2 в точности такая же, как функция BIGGEST2 с очевидной заменой SMALLEST2 на BIGGEST2 и A'lAX на MIN, то для экономии места она и все ее дальнейшие варианты будут нами опущены.