К главе 13

Задача 13.1

Предположим, что нам нужна программа, которая генерирует и изучает некоторое древовидное пространство, подобное тому, которое использовалось в наших примерах прокладки пути по карте. Далее предположим, что каждый город представлен атомом и все соседние города могут быть найдены в списке под свойством NEIGHBORS (СОСЕДИ). Для примера на рис. 17.13.1 имеем:

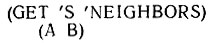
Напишите функцию DEPTH-FIRST (ПОИСК-В-ГЛУБИНУ), которая получает начальный и конечный города, а выдает маршрут, например:

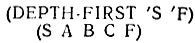
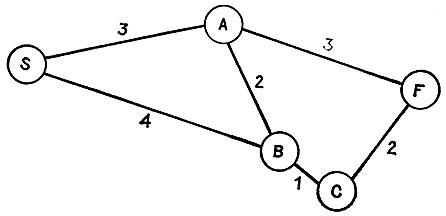
Рис. 17.13.1

Здесь должен использоваться поиск в глубину, поэтому точный маршрут зависит от того, каким образом узлы упорядочены в списке NEIGHBOR. В приведенном примере показанный конкретный маршрут, разумеется, не является кратчайшим.

Задача 13. 2

Напишите функцию BREADTH-FIRST (ПОИСК-В-ШИРИНУ), которая может работать с той же задачей прокладки маршрута, но с использованием поиска в ширину. Вы, вероятно, придете к выводу, что поиск в ширину легче организуется на Лиспе.

Задача 13.3

Сделайте такое обобщение функции BREADTH-FIRST, чтобы получить функцию BEST-FIRST (ПОИСК-С-НАИЛУЧШЕГО), которая двигается от города с кратчайшим расстоянием по воздуху до конечного пункта. Предположите, что положения городов могут быть найдены под свойством COORDINATES (КООРДИНАТЫ). Далее предположите, что земля плоская.

Задача 13.4

Напишите функцию BRANCH-AND-BOUND (ВЕТВИ-И-ГРАНИЦЫ), которая находит оптимальный маршрут от исходного города до пункта назначения, используя метод ветвей и границ.

Задача 13.5

О сложной организационной задаче можно думать, как о сети из подзадач, где стрелка между подзадачами всегда ведет от той задачи, которая должна быть завершена до того, как можно начинать выполнение задачи, на которую указывает стрелка. Из многих путей по такой сети от начала к концу один представляет особый интерес, поскольку он определяет время, необходимое для выполнения всей задачи в целом. Он оказывается критическим путем. Если будет задержка с любой подзадачей на критическом пути, то и весь проект будет задержан.

Часть 1. Напишите функцию CRITICAL-PATH (КРИТИЧЕСКИЙ- ПУТЬ) для определения критического пути. Предположите, что атомы представляют собой подзадачи. Отношения между задачами обозначаются свойством NEXT-TASKS (СЛЕДУЮЩИЕ-ЗАДАЧИ), а требуемые для выполнения времена - свойством TIME (ВРЕМЯ). Часть 2. Можно ли улучшить вашу функцию за счет применения метода ветвей и границ?

Задача 13.6

Функции BIGGEST (НАИБОЛЬШИЙ) и SMALLEST (НАИМЕНЬШИЙ) были объединены нами в одну функцию MINIMAX. Чтобы быть уверенным, что все понято до конца, повторите построение функций BIGGEST1 и SMALLEST 1.

Задача 13.7

В одной из предшествующих глав была приведена формула для ограничения поиска путем уменьшения степени ветвления по мере того, как растет глубина и снижается оценка перспективности:

Снова модифицируйте функцию MINIMAX, но на этот раз так, чтобы число последователей, рассматриваемое в каждом узле, было бы наименьшим из числа, даваемого приведенной формулой, и числа, возвращаемого функцией PLAUSIBLE-MOVES (ПЕРСПЕКТИВНЫЕ-ХОДЫ). Предположите, что список, возвращаемый функцией PLAUSIBLE-MOVES, устроен так, что ходы в нем упорядочены, начиная с самого перспективного и кончая наименее перспективным.

Задача 13.8

Функция MINIMAX берет отрицание переменной NEW-VALUE (НОВОЕ-ЗНАЧЕНИЕ) и возвращает результат. Как изменилась бы игра, если бы по ошибке этот этап отрицания был опущен? Было бы тогда проведено в среднем больше или меньше статических оценок?

Задача 13.9

Во многих игровых деревьях различные последовательности ходов приводят к одному и тому же положению на доске. Измените функцию MINIMAX так, чтобы учесть это обстоятельство. Вы можете предполагать, что позиции в игре хранятся в форме s-выражений, так что две позиции одинаковы, если примененная к ним функция EQUAL возвращает Т.

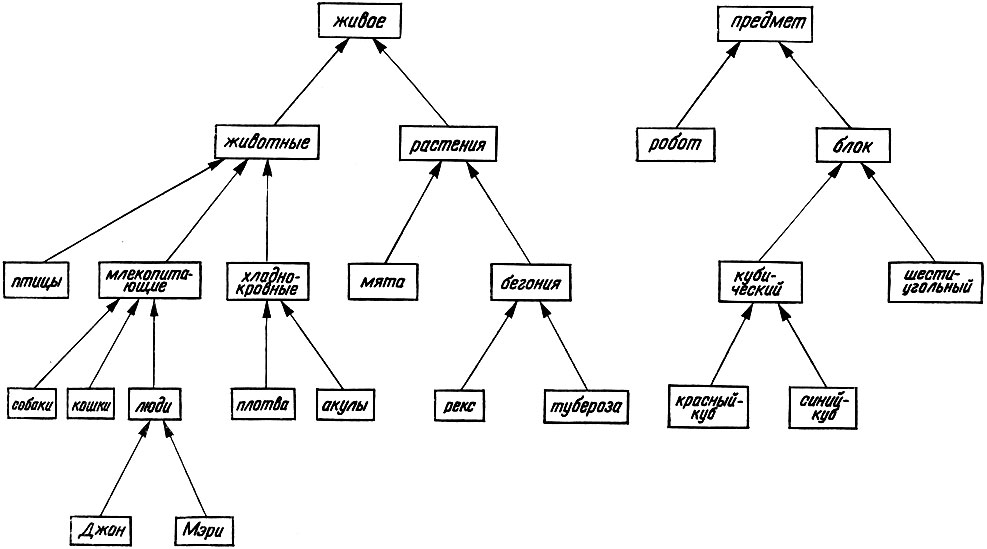
Рис. 17.13.10.1

Задача 13.10 (сформулирована Марком Лейвином)

Настоящая проблема поиска (перебора) связана с некоторым типом структур, известных под названием сети IS-A (т.е. сети типа ЯВЛЯЕТСЯ). Такая сеть часто используется для того, чтобы показать отношения между классами и подклассами объектов. Примером может служить система Линнея в биологии.

Сети типа IS-А могут быть представлены графически, как показано на рис. 17.13.10.1. Такая сеть может, в частности, означать, что кошка ЯВЛЯЕТСЯ млекопитающим и собака ЯВЛЯЕТСЯ млекопитающим. Она также может быть интерпретирована и так, что множество собак и множество кошек являются подмножествами множества млекопитающих.

Сеть типа IS-A может быть реализована в структурах Лиспа многими способами. Предположим, что узлы сети представлены атомами, а отношения IS-A представлены посредством списков свойств. Для приведенной сети было проделано что-то вроде следующего:

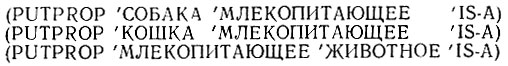
ЗАМЕЧАНИЕ! В частях 1, 2 и 3 настоящей задачи предполагается, что для каждого узла X в сети типа IS-A имеется самое большее один (а может быть, и ни одного) узел Y, такой, что X IS-A Y; точно так же циклы из указателей IS-A недопустимы.

Часть 1. Объясните на обычном языке, что делает следующая программа на Лиспе, когда ей предъявляются два узла NODE1 и NODE2 из сети типа IS-A в качестве аргументов, причем можете предполагать, что сеть представлена так, как было сказано выше, и что она была построена с использованием большого количества функций PUTPROP. Предположим, что функция ALLNODES ВСЕ-УЗЛЫ) возвращает список всех атомов, которые представляют собой узлы в дереве типа IS-A. См. стр. 493.

Часть 2. Эта часть вопроса связана с сетью типа IS-A, изображенной на рис. 17.13.10.1. Укажите результат оценивания каждого из следующих выражений, основанный на вашем объяснении работы программы в части 1:

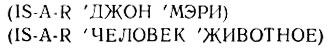
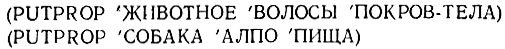
Часть 3. Одной из главных причин использования сети типа IS-A является то, что это удобный и компактный способ связывания свойств с классами и подклассами. Взгляните на рис. 17.13.10.2. Эти свойства могли бы быть реализованы в системе Лисп путем помещения их в списки свойств атомов, представляющих узлы:

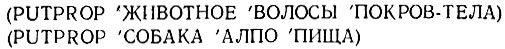
Распространенная договоренность состоит в том, что свойства унаследуются от суперклассов; например, так как (СОБАКА ЯВЛЯЕТСЯ ЖИВОТНОЕ), то мы можем заключить, что СОБАКА имеет ВОЛОСЫ, как значение "неявного" свойства ПОКРОВ- ТЕЛА.

Напишите простую функцию на Лиспе, называемую 1S-A-GET, которая работает аналогично стандартной функции Лиспа GET, но с особенностью, описанной выше; она должна давать в качестве результата что-то вроде

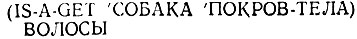
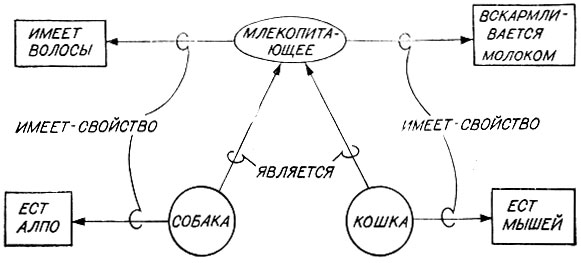
Рис. 17.13.10.2

Часть 4. В частях 1-3 мы ограничились сетями типа ЯВЛЯЕТСЯ, в которых из каждого узла допускалась лишь одна связка типа IS-A. Однако возможно, мы захотим ослабить ограничение и допустить кратные указатели типа IS-A. Приведите соображения за и против реализуемости и необходимости такой модификации. Часть 5. Предположим, что вопреки (или в согласии с) вашей аргументацией в части 4 мы решили допустить кратные указатели типа IS-A, предположив, что свойство IS-A может иметь в качестве значения список

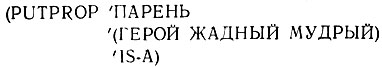
Кратко опишите, как это изменение скажется на программе IS-A-R из части 1 (нашей программе) и на программе IS-A-GET из части 3 (вашей программе),