К главе 14

Задача 14. 1

Приведенная функция MATCH (СОПОСТАВЛЕНИЕ) работает с образцами и элементами данных лишь в форме списков. Она не может сопоставлять данные и образцы, являющиеся списками списков. Измените слегка функцию MATCH так, чтобы обеспечить работу в более общем случае, включающем вложенные структуры образцов и данных. Например, сопоставление должно быть успешным в следующем случае:

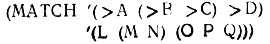
Значением А, которое здесь должно появиться, должно быть L; В - М, С - N, a D - (О Р Q).

Задача 14.2

Используйте методику функции MATCH, дополнив программу так, чтобы построить рекурсивную программу, преобразующую инфиксную арифметическую нотацию в префиксную нотацию языка Лисп. Предположите, что операторы f, o , /, + и - соответствуют функциям Лиспа: EXPT, TIMES, QUOTIENT, PLUS и DIFFERENCE.

S-выражения в инфиксной нотации должны преобразовываться в s-выражения со стоящими впереди операторами, как в следующем примере:

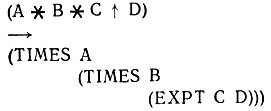
Несомненно, вы будете пользоваться функцией COND. Попытайтесь сделать так, чтобы первое предложение оканчивало дальнейшую обработку на выражениях, состоящих только из атомов. Тогда второе предложение может работать со списками из лишь одного элемента и поэтому без операторов. При этом рекурсия просто направляется в этот элемент. Например, 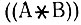- это s-выражение, воспринимаемое в качестве такого элемента, и это приводит к рекурсивному вызову .

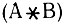Остающиеся предложения будут проверяться на присутствие различных операторов. Их порядок в COND определяет иерархию операторов, принятую в инфиксной нотации. При обнаружении оператора строится новое выражение из имени соответствующего префиксного оператора и результатов преобразования его аргументов в префиксную форму. Например,s-выражение 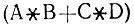вызывает конструирование следующего нового s-выражения⁸:

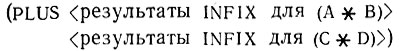
или

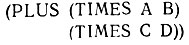
^* (INFIX-название функции, преобразующей нотацию.- Прим. перев)

Задача 14.3

Теперь мы построим несколько упрощенный вариант системы сопоставления, используемой в программе Эванса на геометрическую аналогию. Предположим, что GEOMATCH (ГЕОМЕТРИЧЕСКОЕ- СОПОСТАВЛЕНИЕ) - это функция двух аргументов, каждый из которых является списком отношений, таких, как

Функция GEOMATCH должна найти такой способ объединения переменных в пары, при котором эти два списка имеют наибольшее пересечение. Функция GEOMATCH должна возвращать число элементов в этом максимальном пересечении.

Нормально функция GEOMATCH будет работать с выходом функций, генерирующих правила, которые будут обращаться к численным описаниям геометрических фигур. Эти функции, генерирующие правила, вырабатывают выход, который отличается от исходных образцов в двух существенных моментах. Во-первых, в каждом правиле три множества отношений, а не одно. Во-вторых, появляющиеся атомы будут выглядеть несколько необычно: поскольку они создаются внутри системы, то это будут не буквы L, М и т. д., а, скажем, G 0012.

Часть 1. Напишите функцию PICK (ВЫБРАТЬ), которая будет возвращать список переменных, найденных в списках отношений, подобных приведенным выше.

Часть 2. Напишите функцию, которая принимает два списка атомов равной длины и вырабатывают их объединения в пары всеми возможными способами. Для каждого из способов возвращаемое значение должно содержать список из двухэлементных списков, как в приведенном примере:

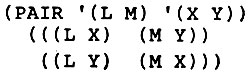
Часть 3. Функция SUBST представляет собой функцию Лиспа от трех аргументов, которая осуществляет подстановку одного s-выражения вместо второго, когда оно встречается в третьем. Рассмотрим следующее:

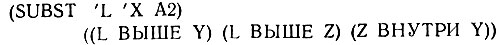
Напишите функцию SUBSTITUTE (ПОДСТАВИТЬ), которая выполняет подстановку списка отношений, используя список пар атомов. Требуется, например, следующее:

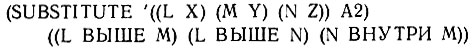
Часть 4. Когда подстановки сделаны, то с помощью функций Лиспа LENGTH и INTERSECTION^* можно определить степень соответствия между двумя списками при использованном методе образования пар. Имейте это в виду при написании функции GEOMATCH.

^* (Функция INTERSECTION, видимо, случайно упущена автором в персчпе основных функций Лиспа. Однако по ее смыслу (ПЕРЕСЕЧЕНИЕ) она должна выделять в отдельный список те элементы s-выражений, которые у них являются общими.- Прим. перев.)

Задача 14.4

Иногда более короткий список сопоставим с более длинным в том отношении, что все элементы короткого списка имеются в длинном списке, причем входят они в том же порядке. Таким образом, в этом смысле список (А В С) успешно сопоставляется со списком (А X V В Е С).

Часть 1. Напишите функцию М, которая проверяет списки в указанном смысле.

Часть 2. Распространите действие функции, составленной в части 1, на случай, когда в коротком списке используются переменные типа > и <. Переменные типа > должны получить значения, а переменные типа < должны быть заменены на такие значения.

Часть 3. Распространите эту функцию сопоставления на случай, когда элементами списков могут быть списки атомов, а не только атомы. Предположите, что символы > и < могут появиться на любом уровне. Сопоставление такого рода необходимо в элементарной системе продукций, когда образец, соответствующий правилу продукции, сопоставляется с содержимым кратковременной памяти.

Часть 4. Вы, вероятно, составили функцию сопоставления так, что она дает следующие результаты:

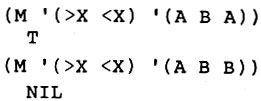
Можно было бы привести соображения в пользу того, что во второй ситуации также должен быть результат Т, интерпретируемый так, что первый элемент в длинном списке, А, не принимается во внимание, X затем принимает значение В через переменную >Х, и поэтому <Х сопоставляется с В. Измените функцию так, чтобы в обоих приведенных выше ситуациях возвращалось бы значение Т. По-видимому, полезно будет вспомнить, как были реализованы переменные типа *.

Задача 14.5

Рассмотрим следующую алгебраическую задачу. Не смущайтесь отсутствием единиц измерения - предположите, что все числа даны в соизмеримых единицах:

(ДОЖДЬ В ИСПАНИИ ЗАНИМАЕТ УДВОЕННОЕ РАССТОЯНИЕ МЕЖДУ ТОЛЕДО И МАДРИДОМ Р ДОЖДЬ В ИСПАНИИ ИДЕТ ГЛАВНЫМ ОБРАЗОМ НА РАВНИНАХ Р СКОРОСТЬ МОЕЙ МАШИНЫ РАВНА 20 Р ВРЕМЯ НЕОБХОДИМОЕ ЧТОБЫ ДОБРАТЬСЯ ИЗ ТОЛЕДО ДО БАРСЕЛОНЫ РАВНО 7 Р КАКОВ ДОЖДЬ В ИСПАНИИ Q)

Найдите систему уравнений, которые были бы построены. Укажите на все аспекты задачи, которые заставят программу Боброва STUDENT использовать информацию, не содержащуюся в самой формулировке. Даст ли программа правильный ответ, неправильный ответ или никакого ответа? Дайте пояснения.

Задача 14.6

В общих чертах, каким образом функции сопоставления можно было бы использовать для реализации подхода GPS при работе в некоторой конкретной предметной области.