1.4. Выбор операторов изображения

После того как для анализа данных выбран критерий качества, можно сравнивать два или несколько операторов изображения с помощью этого критерия. Можно даже искать оптимальный оператор изображения, минимизирующий значение соответствующего критерия. Тогда мы сталкиваемся, во-первых, с необходимостью рассмотреть вопросы существования и единственности оптимума, и, во-вторых, с отысканием аналитического и вычислительного решений; второй этап обычно составляет основную часть задачи. Мы будем заниматься этими проблемами по мере их возникновения в связи с изучением конкретных типов структур образов в следующих главах. В данном разделе ограничимся всего лишь несколькими простыми замечаниями общего характера.

Характер множества допустимых операторов изображения F зависит от того, какие вычислительные средства имеются в нашем распоряжении. Допустим, что множество F имеет самый общий вид и на него наложено только одно слабое ограничение условие 1.2.1.

Пусть множество - счетное, индексированное с помощью υ = 1, 2, . . ., и пусть используется критерий вида (1.3.12). В таком случае функция f может принимать значения I₁, I₂, ...; введем подмножества множества

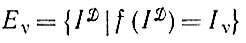(1.4.1)

и на основании соотношения (1.3.12) получаем

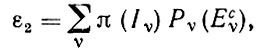(1.4.2)

где π(I_ν) - априорные вероятности и P_ν -распределения вероятностей dI для I = I_ν. Если распределения вероятностей P_υ абсолютно непрерывны относительно некоторой меры μ (соответствующие производные Радона - Никодима обозначены через p_ν), то выражение (1.4.2) принимает следующий вид:

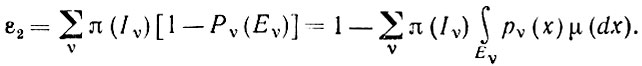(1.4.3)

Пусть e_ν(х) - индикаторные функции подмножеств E_ν, так что

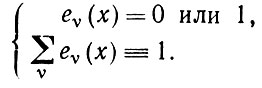(1.4.4)

Таким образом, для минимизации значения ε₂ необходимо разрешить относительно функций ε_ν выражение

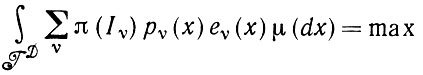(1.4.5)

с учетом (1.4.4). Хорошо известно, что максимум достигается при следующих условиях:

(1.4.6)

где

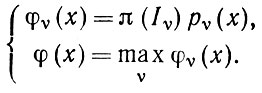(1.4.7)

Другими словами, необходимо выбирать

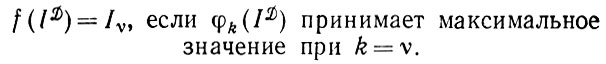(1.4.8)

Здесь нет ничего нового - это прекрасно известный результат из теории бейесовского вывода. Нетрудно также проверить единственность решения. Следует, однако, заметить, что бейесовский оператор изображения (1.4.8) не так уж хорош, как может показаться. Во-первых, он применим лишь к счетным алгебрам изображений. Во-вторых, он предполагает использование бсйесовского подхода, что невозможно при отсутствии сведений об априорных вероятностях.

Если априорные вероятности не заданы, можно попробовать воспользоваться правдоподобным оператором изображения

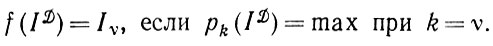(1.4.9)

Это выражение основано на неявном допущении, согласно которому все идеальные изображения равновероятны. Если множество бесконечно, то это допущение даже не является логически непротиворечивым.

Аналогично, если множество не является счетным, но постулируется непрерывность с плотностями распределений р_I то выражение (1.4.9) можно заменить следующим:

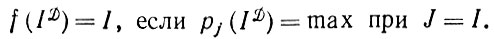(1.4.10)

Чтобы упростить рассуждения, будем считать максимум единственным.

Из классической теории статистического вывода известно, что оценивание по методу максимального правдоподобия (а именно эта процедура и представлена выражением (1.4.10)) обладает рядом привлекательных свойств. Особенно важны в этом отношении асимптотические свойства оценок по максимальному правдоподобию (см., например, монографию Крамера (1946), гл. 33). Подобным же образом, уравнение (1.4.8) представляет собой в сущности критерий Неймана -Пирсона (см. монографию Крамера (1946), гл. 35).

Здесь, однако, следует проявлять определенную осторожность. Классическая теория статистического вывода имеет дело преимущественно с независимо идентично распределенными событиями в конечномерных пространствах. В анализе образов объекты изучения не должны обязательно быть конечномерными, и свойство независимой идентичной распределенности не обязательно должно выполняться. Известно несколько обобщений для случаев, когда наблюдаемые объекты принадлежат бесконечномерным функциональным пространствам (см., например, работу автора (1950)), но они не всегда соответствуют нашим задачам.

Следовательно, обращаясь к методам максимального правдоподобия, необходимо изучать получаемые операторы изображения по мере их появления и оценивать их качество применительно к конкретным ситуациям вместо того, чтобы пытаться использовать широко известные теоремы.

Допустим, что мера μ S-инвариантна и деформации ковариантны по вероятности (см. т. 1, разд. 4.1). Тогда для произвольного преобразования подобия s справедливо следующее:

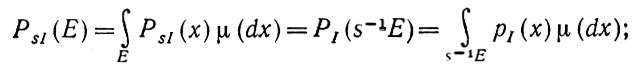(1.4.11)

подстановка sx = y приводит к следующему уравнению:

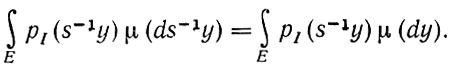(1.4.12)

Следовательно, почти всюду справедливо уравнение

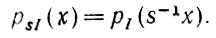(1.4.13)

Это означает, однако, что правдоподобный оператор изображения f, удовлетворяющий условию (1.4.10), обладает свойством:

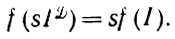(1.4.14)

Если, другими словами, мера μ S-инвариантна и механизм деформации ковариантен по вероятности, то (единственный) правдоподобный оператор изображения будет инвариантным (см. разд. 1.2).

Существенный интерес вызывает случай, когда производную Радона - Никодима можно представить как убывающую функцию расстояния между идеальным и деформированным изображениями:

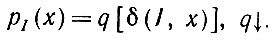(1.4.15)

Из выполнения условия (1.4.15) непосредственно следует, что правдоподобный оператор изображения представляет собой процедуру восстановления по принципу минимального расстояния:

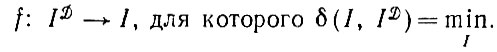(1.4.16)

Далее, если δ, входящее в условие (1.4.15), инвариантно (см. т. 1, разд. 4.1), то, как и выше, можно считать, что оператор if также инвариантен.

Не так часто встречается случай, когда I^D = dI и I совместно определяют d, а производная Радона - Никодима является убывающей функцией усилия деформации d. В таком случае правдоподобный оператор изображения f можно считать решением, соответствующим минимальному усилию деформации:

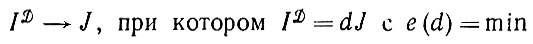(1.4.17)

(при этом, естественно, сохраняется допущение об однозначном определении минимума). Если функция усилия деформации инвариантна, то из этого снова следует, что соответствующий оператор изображения f будет инвариантен.