1.3. Критерии качества для операторов изображения

Качество оператора изображения будет оцениваться с помощью численного критерия. В данном разделе мы рассмотрим несколько возможностей; для того чтобы сформулировать основные положения, мы сосредоточимся на восстановлении изображений. Для операторов изображений других типов следует ввести соответствующие модификации.

Мы будем полагать в данном разделе, что условие (1.2.1) выполняется. Введем оператор изображения f: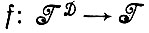 и рассмотрим величину

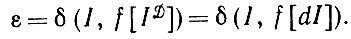(1.3.1)

Эта величина зависит от идеального изображения I и деформаций d. Если и I, и d фиксированы, но, естественно, неизвестны, то ε -неотрицательное число. При сравнении двух операторов изображения f и f' можно сопоставлять соответствующие значения ε и ε', т. е. определять, какое соотношение выполняется: ε<ε', ε = ε' или ε>ε'. Результат такого сравнения вполне может зависеть от того, каковы идеальное изображение I и деформации d, так что мы не получаем оснований для предпочтения одного оператора изображения другому. Эта проблема однородности хорошо известна благодаря классической теории статистики. Если результат сравнения не зависит от характераI и d, а это бывает редко, то для того, чтобы улучшить постановку задачи и обеспечить однозначность ответа, необходимо привлечь какой-либо дополнительный принцип.

Это можно сделать, например, когда на множестве деформаций определена вероятностная мера (см. (1.4.1)), так что значение ε можно рассматривать как случайную величину. В таком случае естественно интерпретировать значение ε в некотором усредненном смысле, т. е. использовать в качестве окончательного критерия некоторый параметр сдвига или параметр шкалы ε₁ распределения ε. Обычно мы будем делать это следующим образом:

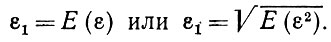(1.3.2)

Это не всегда позволяет полностью снять проблему однородности, поскольку критерий ε₁ может также зависеть от идеального изображения. Если априорная мера на 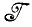известна, то можно также обратиться к усреднению, например, вида

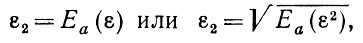(1.3.3)

где индекс а обозначает, что интегрирование производится как по мере, заданной на деформациях, так и по мере, заданной на идеальных изображениях. Другими словами, при решении задачи используется бейесовский подход. Таким образом ε₂ становится числом, и при выборе из нескольких конкурирующих операторов изображения появляется возможность прибегать к сравнению.

В таком случае, если ε₂ → 0 по мере накопления все большего количества информации, есть основания говорить о состоятельном восстановлении изображения. Требование состоятельности процедуры восстановления является слабым, и обычно мы будем стремиться к получению более информативных результатов.

Приведем несколько примеров функций расстояния, которыми мы будем пользоваться. Если параметризация 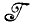^* задается булевым вектором x = (x₁, x₂, ...,x_d), в качестве критерия можно воспользоваться расстоянием Хемминга

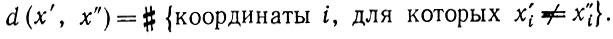(1.3.4)

Этот критерий приписывает всем координатам булева вектора равные веса, и при усреднении бейесовским методом мы получаем, что

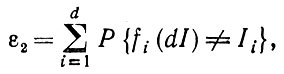(1.3.5)

с аналитической точки зрения изящное выражение.

При работе с изображениями-множествами в некотором опорном пространстве X с ограниченной метрикой можно было бы в качестве функции расстояния 6 использовать расстояние Хаусдорфа

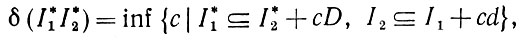(1.3.6)

представленное с помощью функции расстояния опорного пространства X (см. т. 1, с. 153).

Альтернатива, к которой мы будем часто прибегать, когда на опорном пространстве X задана ограниченная мера m, заключается в использовании величины

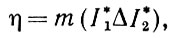(1.3.7)

где Δ обозначает симметрическую разность

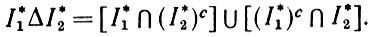(1.3.8)

Обозначив индикаторные функции через i₁(x) и i₂(x) соответственно и учитывая, что i²₁(x) ≡ i₁(x), получаем

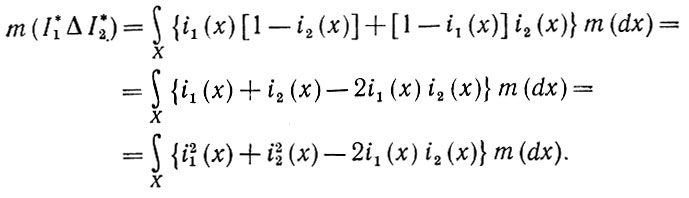(1.3.9)

Следовательно,

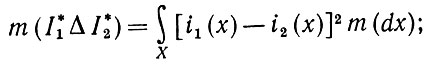(1.3.10)

таким образом, мы имеем квадрат 12-нормы. Тогда функцию расстояния мы получаем, положив

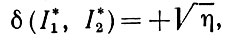(1.3.11)

что опять-таки привлекательно с аналитической точки зрения.

С другой стороны, если деформированные изображения образуют дискретное множество, то может оказаться естественным воспользоваться расстоянием дискретной топологии

(1.3.12)

Тогда просто получаем, что

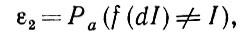(1.3.13)

и, таким образом, этот критерий отражает вероятность обеспечения корректного восстановления изображения при использовании оператора f.

Редко имеет смысл применять критерий (1.3.13), когда множество 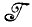^* не является дискретным. Это так по крайней мере, когда распределение вероятностей f(dI) при фиксированном I непрерывно, поскольку в таких ситуациях вероятность корректного восстановления, очевидно, равна нулю. Можно, конечно, в подобных случаях исходить из плотности вероятности p_I(х) результата применения оператора изображения f(dI) для идеального изображения f при x=I. Результат применения такого критерия интерпретировать нелегко, за исключением тех частных случаев, когда вид функции р придает значению критериев ясный смысл. Это не имеет непосредственного отношения к функции расстояния.

Выбор критерия значительно упрощается, когда ^* - (сепарабельное) банахово пространство. При этом можно пользоваться нормой ||⋅|| и применять L_p-критерии типа

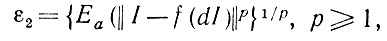(1.3.14)

используя преимущества свойств линейности банахова пространства.

Допустим, например, что изображение и его деформированный вариант заданы полями комплексных чисел на плоскости (см. т. 1, разд. 4.6). Оператор восстановления f будет в этом случае преобразовывать поле I^d=dI в некоторое другое поле f(dl). Полная интенсивность разностного поля будет равна при этом

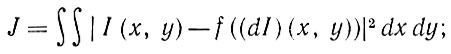(1.3.15)

так что, если считать ^* гильбертовым пространством, критерий Е(J) можно получить в виде ε₂ (1.3.14) при р = 2.

Возвращаясь к общему случаю условия 1.2.1, допустим, что на пространстве деформаций задана инвариантная функция усилия (т 1, разд. 4.1). Для заданного оператора изображения f рассмотрим уравнение относительно деформаций d'∈D:

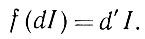(1.3.16)

Это уравнение может иметь одно или несколько решений либо не иметь их вообще. Множество решений Е = Е (d, I; f) зависит от d и I и, естественно, от самого оператора изображения. Запишем следующее выражение:

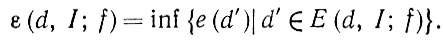(1.3.17)

Если Е (d, f; I) = ∅, положим ε = +∞.

Величина (1.3.17) характеризует величину усилия, необходимого для преобразования посредством деформации идеального изображения в изображение, соответствующее восстановленному значению f(dl). Естественно, следовательно, ввести критерий

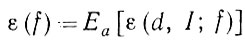(1.3.18)

и сопоставлять операторы изображения, исходя из их значений ε(f).

Заметим, что, считая пару (f(I^D), I) симметрической (аналогично тому, как это делалось в теореме 4.1.1, т. 1), можно было бы вернуться к критериям, основанным на функции расстояния.