Глава 2. Анализ абстрактных образов

2.1. Парадигматические деформации

В разд. 2.1-2.3 мы рассмотрим (линейные) изображения-последовательности, содержащие отвлеченные символы. Конфигурации, однако, не обязательно должны иметь линейный тип соединения; мы будем изучать, что происходит при применении к ним различных механизмов деформации.

Простейший случай когда образующие являются символами некоторого заданного алфавита, т. е. представляют собой "буквы" или "слова" некоторого языка, и Σ - линейный" с отношением согласования ς - "истина". Это означает, что мы имеем дело с абсолютно неструктурированным случаем, который описан в начале разд. 3.2 т. 1, и, следовательно, изображение -это просто произвольная цепочка символов, а группа преобразований подобия S - группа подстановок.

Обозначим образующие через 1, 2, ..., n и соответствующие вероятности через q_i, i= 1,2, ..., n. Удобно считать, что вероятности q упорядочены по не убыванию. Вероятностная мера на 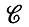_n - это просто Р-мера, соответствующая n независимо идентично распределенным переменным, принимающим значения в G.

Пусть деформации 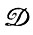вносят в конфигурации такие смещения (как это было описано в Случае 4.2.1, т. 1), что символы алфавита переставляются путем применения одного из преобразований подобия s₀∈S. Нам не известно преобразование подобия s₀, и мы хотим найти метод восстановления идеального изображения.

Здесь мы имеем дело с обычным шифром, и интуитивно очевидно и давно известно, как восстанавливать идеальное изображение I исходя из деформированного изображения I^D. Менее очевидным может оказаться то, почему этот метод в некотором смысле оптимален, так что мы бегло обсудим эту проблему и ряд связанных с ней вопросов, прежде чем перейти в следующем разделе к изучению более интересных случаев.

Мы попытаемся определить обратное преобразование s^-1₀ с помощью критерия вида (1.4.10), т. е. воспользуемся процедурой распознавания, основанной на методе максимального правдоподобия. Если s-преобразование подобия, с помощью которого реализуются 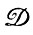, то для деформированного изображения

I^D = (j₁, j₂, ..., j_n) = s (i₁, i₂, ..., i_n) справедливо следующее:

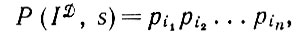(2.1.1)

или, в более компактном виде,

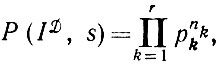(2.1.2)

где n_k - число случаев появления символа k. Наблюдению поддаются j, но не i, так что для максимизации правдоподобия следует минимизировать следующую сумму:

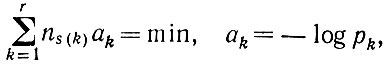(2.1.3)

где s(k) - это k-й элемент преобразованного алфавита. Если некоторые p_k = 0, то соответствующие символы просто удаляются из алфавита.

Решение уравнения (2.1.3) не вызывает никаких затруднений (см. монографию Харди, Литлвуда и Пойа (1934), гл. 10). Поскольку последовательность a_k невозрастающая, нам остается просто найти подстановку, которая делает n_s(k) неубывающей. Оператор изображения принимает в этом случае вид обращения этой подстановки в G, применяемого по отдельности к каждому символу деформированного изображения,- решение, продиктованное обычным здравым смыслом. Если все p_k различные, то нетрудно показать, что вероятность правильного восстановления с помощью данного метода стремится к единице при стремлении n к бесконечности. Этот вид распознавания является, следовательно, состоятельным.

Здесь мы начинали со случая, когда отсутствует структура, затем на ^n{9i) вводилась P-мера, что делало возможным восстановление. В принципе можно было бы перейти к несколько более структурированным случаям аналогично тому, как это делалось в разд. 3.2 т. 1. Если образующие представляют собой переходы k-*l, отношение согласования р означает "равенство", а идеальные изображения все еще остаются цепочками символов заданного алфавита, то мы получаем стационарную марковскую цепь. Пусть Pfoi - вероятности перехода, и существует, скажем, единственное множество nk вероятностей равновесия. Точно такие же соображения, как и выше, позволяют определить подстановку s как решение уравнения

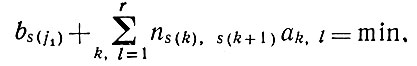(2.1.4)

где b_k = - log π_k и a_k,l = - log p_kl. Преобразование, обратное найденному s, должно затем использоваться для восстановления

идеального изображения. Аналогичным образом дело обстоит и для марковских цепей высших порядков.

Рассмотрим еще один слабо структурированный случай. Пусть множество 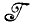определяется заданным конечным списком цепочек, составленных из символов конечного алфавита, и - деформации пульсирующего типа (см. уравнение 4.2.2, т. 1, а также случай 4.2.4, т. 1). Это означает, что все символы цепочки / подвергаются воздействию деформаций независимо. Пустьi → j с вероятностью p_ij, так что

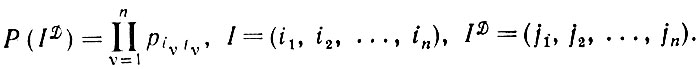
(2.1.5)

Восстановление по методу максимального правдоподобия приводит в таком случае к решению уравнения

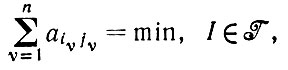(2.1.6)

для фиксированных наблюдаемых значений j при a_kl = - log p_kl. Весьма частный случай уравнения (2.1.6) возникает при

(2.1.7)

так что произвольный символ k не подвергается изменениям с вероятностью 1 - ε. С вероятностью ε этот произвольный символ преобразуется в некоторый другой символ, причем вероятности для r - 1 остальных символов одинаковы. Можно отметить, что эти деформации 3) ковариантны по вероятности, однако деформации, рассмотренные в настоящем разделе выше, не обладают свойством ковариантности. Уравнение (2.1.6) сводится в таком случае к следующему:

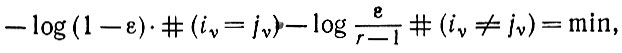(2.1.8)

или при использовании расстояния Хемминга

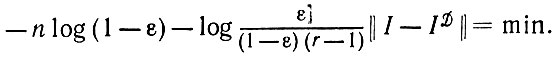(2.1.9)

При ε<(r - 1)/r эта процедура эквивалентна восстановлению по принципу минимума расстояния:

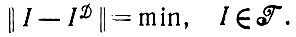(2.1.10)

Этот минимум не всегда единственный.

В качестве списка 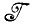может выступать, например, перечень фамилий, возможно записанных в сокращенном виде, как это иногда делается в системах бронирования авиационных билетов.

Деформации возникают из-за ошибок в написании фамилий; они могут появляться также из-за механических ошибок, вызванных неполадками на линиях связи. Человек может сделать ошибку в написании слова, поставив вместо нужной буквы другую, но существуют и другие возможности. К распространенным ошибкам относятся перестановка двух букв, пропуск буквы и введение лишней буквы. Могут встретиться комбинации подобных ошибок, а также и ошибки более сложных разновидностей. Если механизмы деформации удается определить в явном виде, то задачу восстановления можно анализировать математическими средствами, по крайней мере в принципе. Сведения о некоторых ранних работах, посвященных автоматическому исправлению ошибок в написании, читатель может найти в статьях Торелли (1962) и Алберга (1967). Этот вид деформаций, строго говоря, не относится к парадигматическому типу (см. следующий параграф), поскольку деформация может воздействовать одновременно более чем на один символ.

Парадигматическими будем называть такие деформации цепочек, которые воздействуют на отдельные символы цепочки независимо. Предыдущие случаи были слабоструктурированными, теперь же мы обратимся к алгебрам изображений, структурированным синтаксически.

Для того чтобы предельно упростить ситуацию, будем считать, что аналогично разд. 3.2 т. 1 задана алгебра 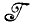, порожденная автоматной грамматикой 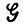с n внутренними состояниями, i = 1 - начальное состояние и i = n + 1 - заключительное

состояние. Переходам поставлены в соответствие определенные выходные символы:

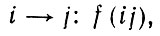(2.1.11)

где все f принимают значения из конечного выходного алфавита {А, В, С, ...}. На множестве цепочек, порождаемых грамматикой, определена вероятностная мера (способ ее задания описан в т. 1).

Допустим теперь, что деформации 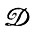действуют следующим образом. Цепочка I = b₁b₂...b_m, порожденная из 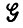с помощью М, является локально искаженной в том смысле, что

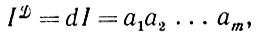(2.1.12)

где a_i = d_ib_i, причем все d_i статистически независимы, а принимают значения из алфавита 5, который может (но не обязательно должен) совпадать с Л. В таком случае 3) полностью определены, если известны все вероятности

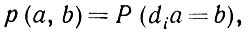(2.1.13)

и мы снова имеем дело с парадигматическими деформациями .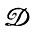

Алгебра изображений 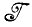и деформации описываются так, как это указано на рис. 2.1.1; мера на вводится с помощью PTRANS. Элементы матрицы TRANS указывают, какой символ поставлен в соответствие данному переходу, т. е. запись t_ij = C означает, что переходу i→j соответствует символ С. Мы ввели фиктивный элемент 0; если переход k→l в данной грамматике не допустим, то это записывается как t_kl = 0. Для того чтобы избежать неоднозначности грамматики , полагаем, что t_ij≠t_ij' при j≠j'. И наконец, ERROR обозначает матрицу вероятностей ошибок, т. е. запись Р (X → Y) характеризует вероятность того, что некоторый символ X в результате деформаций превращается в некоторый другой символ Y. Обычно ожидается, что диагональные элементы матрицы ERROR мажорируют матрицу. Состояние 0, естественно, следует поставить в соответствие нулевой вероятности.

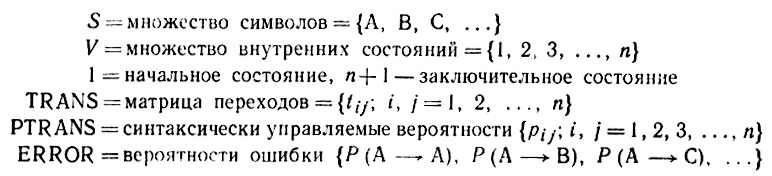
Рис. 2.1.1

Для отыскания оператора изображения мы применяем критерий максимального правдоподобия, и для заданного деформированного изображения I^D = a₁a₂....a_m решаем уравнение

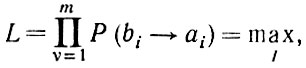(2.1.14)

где максимум берется по всем изображениям I = b₁b₂...b_m∈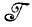, выводимым в заданной грамматике. Эта процедура вполне соответствует проведенному выше рассмотрению, однако здесь необходимо сделать несколько дополнительных замечаний.

Первое носит общий характер. Решая уравнение (2.1.14), мы получаем оператор изображения f, 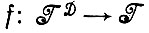. Естественно, может оказаться, что найденное отображение является многозначным. Может оказаться также полезным не просто отыскивать идеальное изображение, максимизирующее значение L, а решать это уравнение для заданного числа изображений f и определять максимально достижимое значение L. Подобная процедура придает оператору изображения f даже еще большую многозначность.

Будем считать оператор изображения f взаимно-однозначным и пусть предъявлено деформированное изображение I^D оказавшееся выводимым в данной грамматике, I^D∈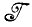. В таком случае мы хотели бы, чтобы выполнялось равенство fI^D=I^D в противном случае нельзя было бы считать такую цепочку допустимой, хотя она и выводима в данной грамматике. Другими словами, мы требуем, чтобы оператор f удовлетворял условию

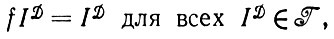(2.1.15)

т. е. оператор изображения должен оставлять неизменными изображения, выводимые в заданной грамматике. При замене уравнения (2.1.14) бейесовским критерием эта проблема становится даже еще более актуальной, поскольку в этом случае "благосклонность" по отношению к обычно встречающимся изображениям увеличивается и, таким образом, необычные, хотя и выводимые в грамматике, изображения будут подвергаться изменениям. Образующими в этой алгебре изображений служат тройки (правила подстановки) i, j, c, поставленные в соответствие ветвям диаграммы состояний конечного автомата (см. Случай 2.4.3, т. 1). Следовательно, деформации 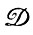можно рассматривать как деформации образующей, сохраняющие показатели связей.

С другой стороны, если используется механизм деформации с (i, j, c) → (i, j, c'), где правая часть также принадлежит одной из ветвей диаграммы состояний, то в результате приложения деформаций цепочки, порождаемые грамматикой, преобразуются в цепочки, порождаемые грамматикой, т. е. 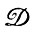- автоморфны (см. разд. 4.1, т. 1). Если выбор конфигурации с' зависит от (i, j), то деформации являются синтаксически зависимыми (см. конец данного раздела).

Третье замечание связано со скоростью вычислений. Решение уравнения (2.1.15) с увеличением m начинает требовать столь большого объема вычислений, что очень скоро становится практически неосуществимым по крайней мере решение "в лоб". Это препятствие можно, однако, обойти, если представить множество 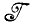в более удобном для обработки виде, что в данном случае можно сделать, заменив идеальные изображения результатами их грамматического разбора. Поскольку в нашем случае синтаксические переменные -это просто внутренние состояния i= 1, 2, 3, ..., n, то изображение I = b₁b₂....b_m следует заменить разложением i, i₂, i₃, ..., i_m+1, причем ограничения сводятся исключительно к тому, что i₁= 1 и i_m+1=n+1. Отсюда следует, что необходимо найти максимум выражения

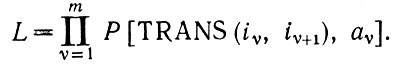(2.1.16)

Здесь все в порядке, поскольку грамматически неправильной последовательности {i_ν} автоматически ставится в соответствие нулевая вероятность с помощью упоминавшегося выше приема с фиктивным терминальным символом 0. Уравнение (2.1.16) хорошо приспособлено, однако, для применения метода динамического программирования. Действительно, введем

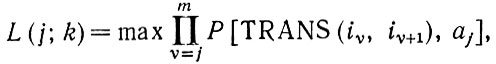(2.1.17)

где максимум берется по последовательностям i_j, i_j+1,...,i_m+1, i_j=k и i_m+1=n+1. В результате приходим к рекурсии

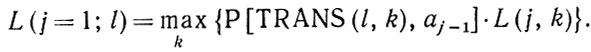(2.1.18)

Пусть k (j, l) обозначает то значение индекса k, при котором достигается максимальное значение (2.1.18) (если таких значений несколько, то соответствующие модификации очевидны). Затем мы решаем уравнение (2.1.18) при j = m, m - 1, m - 2, ..., 2, начиная с

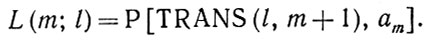(2.1.19)

Тогда правдоподобный оператор изображения позволяет получить

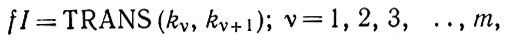(2.1.20)

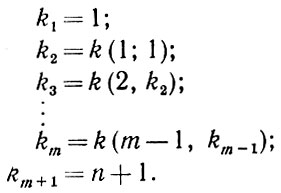(2.1.21)

Чтобы проиллюстрировать, как работает эта схема, мы воспроизвели с помощью ЭВМ идеальные и деформированные изображения, взяв за основу конечный автомат с диаграммой переходов, представленной на рис. 2.1.2, числом состояний n = 4 и символами A, В и С. Предъявлено двадцать идеальных изображений, полученных с помощью модели с синтаксически управляемыми вероятностями.

Была написана еще одна программа, которая позволяла накладывать на идеальные изображения парадигматические деформации; это было сделано при различных вариантах выбора матрицы ERROR. Полученные таким образом деформированные изображения преобразовывались с помощью третьей программы, реализующей процедуру динамического программирования (аналогично (2.1.18)).

Когда уровень вероятностей ошибок составлял величину порядка 10%, оператор изображения f правильно восстанавливал практически все изображения. Деформации обычно имели следующий вид:

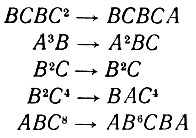(2.1.22)

Когда уровень вероятности ошибок достигал величины порядка 25%, наблюдалось резкое снижение точности работы f и правильно восстанавливалось менее половины изображений. В этом случае мы сталкивались с резкими деформациями типа

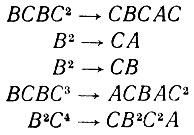(2.1.23)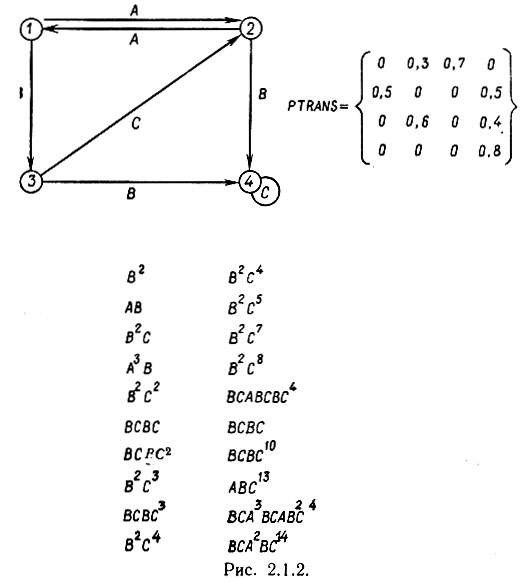

Рис. 2.1.2

Еще одно эмпирически обнаруженное обстоятельство заключалось в том, что, по крайней мере в наблюдавшихся случаях, оператор f не вносил изменений в изображения, выводимые в данной грамматике. Остановимся на этом факте подробнее и допустим, что диагональные элементы матрицы ERROR мажорируют ее в том смысле, что

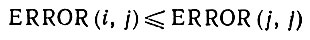(2.1.24)

для любых i, j.

Если дело обстоит именно так, то очевидно, что когда деформированные изображения порождаются данной грамматикой, т. е. I = a₁a₂a₃...a_m∈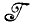, то существует последовательность i₁, i₂,...,i_m+1 такая, что TRANS(i_ν, i_ν+1) = a_ν. Но тогда, однако, всем сомножителям L в уравнении (2.1.14) придается максимально возможное значение при помощи выбора

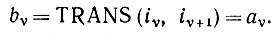(2.1.25)

Если, следовательно, диагональные элементы матрицы вероятностей ошибок мажорируют матрицу, то распознавание, основанное на процедуре максимального правдоподобия, оставляет изображения, выводимые в грамматике, без изменений.

Результаты изучения парадигматических деформаций в случае бесконтекстной грамматики читатель может найти в работе Веласко и де Ренна э Соуса (1974).

Мы ввели допущение о том, что распределение вероятностей изменения символа a → а' не зависит ни от чего, кроме символа а: деформации являются синтаксически независимыми (см. разд. 4.2, т. 1). Если Р(a → а') является также функцией текущего состояния, т. e.

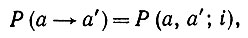(2.1.26)

то деформации все еще остаются парадигматическими, но они уже синтаксически зависимы. Для подобных деформаций оптимальное восстановление изображений мы не изучали.