2.2. Синтаксические деформации

Можно сказать, что парадигматические деформации являются поверхностными, так как они воздействуют лишь на терминальные символы, но не на синтаксические элементы, как это будет иметь место в данном разделе. Здесь, а также в следующем разделе мы будем предполагать, что анализ заканчивается на нетерминальной стадии: нетерминалы рассматриваются здесь как терминальные элементы и мы не будем обращать взимание на превращение нетерминалов в классы терминальных слов с помощью правил лексических вставок. Как и выше, будем считать, что автомат (здесь - заданный на нетерминалах) появляется в стандартной форме с детерминированным ветвлением.

Как и в разд. 3.2 т. 1, алгебра изображений 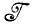состоит из порождаемых грамматикой цепочек с несколькими входными связями i' и несколькими выходными связями i"Г. Поскольку грамматика 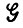детерминированная, то нет необходимости проводить различие между изображениями и конфигурациями, а цепочки также можно рассматривать как последовательности состояний, что будет удобно в нашем последующем изложении.

Обозначим через (i', i") подмножество 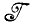с входными связями i' и выходными связями i" при фиксированных i' и i", так что (1, F) обозначает множество порождаемых грамматикой предложений L(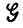), где F обозначает заключительное состояние. Чтобы ввести синтаксические деформации, выделим в 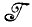некоторые "уязвимые" элементы, которые будем называть сегментами состояний. Сегмент состояния будем обозначать как

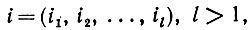(2.2.1)

a используемое множество сегментов состояний - как i. Два сегмента состояний i и j ∈ i пересекаются, если

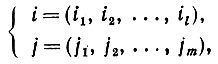(2.2.2)

и

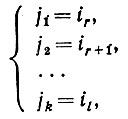(2.2.3)

при r < l; аналогичные соотношения справедливы, когда сегменты i и j меняются местами. Это означает, что сегменты состояний совпадают для внутренних элементов. Единственное ограничение, налагаемое на множество сегментов состояний i, заключается в том, что оно не должно содержать пересекающиеся пары.

Случай 2.2.1 (автоморфные синтаксические деформации). В заданном множестве i непересекающихся сегментов состояний всякому i∈i соответствует случайное отображение в 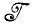(i₁, i₂), где i₁ и i₂ — первый и последний элементы i соответственно. Деформация заданного элемента I∈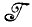(1,F) осуществляется применением этих случайных отображений к каждому содержащемуся в нем сегменту состояния независимо.

Для того чтобы убедиться в осмысленности этой процедуры, допустим, что I = (i₁, i₂, ..., i_l) при i_l = 1, i_l = F. Может оказаться, что I не содержит ни одного сегмента состояния, принадлежащего i, в таком случае I остается точно таким же, каким оно было.

Если же, с другой стороны, I содержит один или несколько сегментов состояний, принадлежащих I, они не могут пересекаться, так что I можно представить единственным образом в качестве однозначно определенной конкатенации:

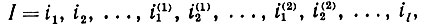(2.2.4)

где i⁽¹⁾ = (i₁⁽¹⁾, i⁽¹⁾₂,... ) и т. д. принадлежат i. Сегменты состояний могут иметь общие концевые точки, но не имеют внутренних пересечений. Поскольку сегменты состояний, принадлежащие I, однозначно определены, то имеется точно заданное распределение вероятностей на 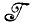(1,F), и это определяет деформирующий механизм. Очевидно, что идеальные изображения при наложении этих деформаций переходят в идеальные изображения, т. е. деформации 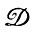автоморфны.

Подобные деформации можно рассматривать как изменения в стиле. Человек, когда он говорит или пишет, может предпочитать те или иные стилистические механизмы, выражающиеся в виде цепочек синтаксических переменных. Это не идет вразрез с правилами грамматики 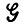, но изменяет стилистические параметры (см. т. 1, с. 95).

Рассмотрим в качестве примера грамматику, представленную в табл. 3.2.1, т. 1. Пусть i включает два сегмента (4,6) и (4, 5, 6) и отображения определены следующим образом:

(2.2.5)

Поверхностные изменения, вызванные этими деформациями 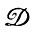, будут заключаться в переходе цепочек (1) и (2, 2) друг в друга, однако изменения эти зависят от того, в какой части синтаксического вывода появляется соответствующая цепочка.

В случае 2.2.1 идеальное изображение, принадлежащее 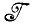в целом при приложении 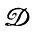изменениям не подвергается. Диффузный образ, однако, определенный синтаксически управляемыми вероятностями на 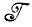(1, F), вообще говоря, будет преобразован в другой диффузный образ. Более того, новый диффузный образ необязательно должен принадлежать классу синтаксически управляемых вероятностей, так как критическое допущение о статистической независимости ветвления может оказаться нарушенным. Автор полагает, хотя и не доказал этого, что если разрешить добавлять новые состояния, то новый диффузный образ можно по-прежнему рассматривать как синтаксически управляемую вероятностную меру, заданную на расширенной слабо эквивалентной грамматике. Новая грамматика необязательно должна быть стандартной формы, как в разд. 2.6 т. 1.

Отметим попутно, что при 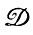, не равном единичному оператору, деформации могут и не оказывать влияния на идеальный диффузный образ. В приведенном выше примере эта ситуация возникает, если для идеального образа имеет место Р (4 → 6) = p₁ и P (4 → 5 → 6) = p₂, где

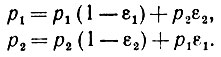(2.2.6)

Очевидно, этот случай - сугубо исключительный.

Введем множество цепочек j, состоящее из всех цепочек, принадлежащих множеству сегментов состояний i, и всех цепочек, принадлежащих носителю вероятностной меры, индуцированной рассмотренными выше случайными отображениями. Будем полагать, что цепочки множества j не имеют пересечений в своих внутренних элементах.

В данном случае восстановление изображения не является нашей целью, поскольку на самом деле деформации не есть "ошибка", которую необходимо было бы компенсировать. Вместо этого мы рассмотрим, каким образом можно с помощью простого алгоритма организовать распознавание двух упоминавшихся диффузных образов.

К решению этой задачи можно подойти на основе стандартных статистических методов. Располагая множеством наблюдений, т. е. предложениями I₁, I₂,...,I_n, принадлежащими 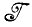(1, F) = L(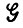), с помощью грамматического разбора разлагаем их на конечные i-цепочки и проверяем гипотезу о том, что деформации 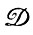не были наложены. Это можно было бы сделать при помощи разбиения L($) на конечное число более или менее произвольных множеств и вычисления вероятности всех множеств относительно проверяемой гипотезы и последующей проверки ее по критерию χ².

Хотя подобная процедура вполне разумна, в ней не используются по существу имеющиеся у нас сведения о 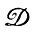. Структурированному подходу, свойственному общей теории образов, более свойственно непосредственное сопоставление индуцированных вероятностных мер друг с другом (см. разд. 2.1).

При реализации этого подхода для упрощения вычислений можно воспользоваться следующей леммой.

Лемма 2.2.1. В основу алгоритма, позволяющего разделить (распознать) два диффузных образа, можно положить достаточную статистику чисел n_j где j- произвольная цепочка, принадлежащая множеству j.

Доказательство. Во-первых, статистика {n_j} однозначно определяется по I₁, I₂, I₃,...,I_n. Действительно, разбиение на i-цепочки, полученное в результате грамматического разбора, единственно, так как 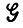детерминистская. Во-вторых, для заданной i-цепочки необходимо учитывать лишь под цепочки с заданным начальным и конечным состоянием, а для таких под цепочек не существует пересечений допустимых цепочек множества j, и потому числа n_j однозначно определены. Для того чтобы продемонстрировать достаточность статистики {n_j}, представим правдоподобие наблюдаемой i-цепочки (k₁, k₂, ...) как

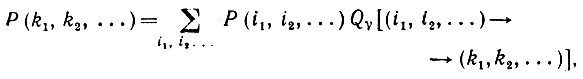(2.2.7)

где γ = 0, если 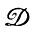не налагались, и в противном случае. Случайное отображение в Q_γ является при γ = 0 тождественным, а при γ = 1 определяется через 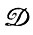. Для наблюдаемой k = (k₁, k₂...) находим под цепочки k⁽¹⁾, k⁽²⁾,..., принадлежащие j, и разлагаем i = (i₁, i₂, ...) как

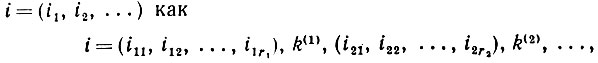(2.2.8)

так что

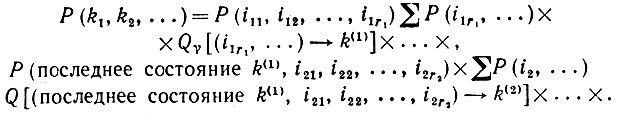(2.2.9)

Из уравнения (2.2.9) следует, что можно записать

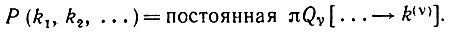(2.2.10)

Эта величина для определенного наблюдаемого изображения зависит только от числа появлений k⁽¹⁾, k⁽²⁾, .... Проведя группировку множителей в правой части уравнения (2.2.9), получаем, что правдоподобие полного множества изображений I₁, I₂, I₃,... , является функцией числа появлений. Таким образом, утверждение леммы о достаточности статистик {n_j} доказано.

В примере (2.2.5) необходимо подсчитать лишь

(2.2.11)

и положить эти две оценки в основу алгоритма распознавания. Тогда правдоподобие с точностью до мультипликативной постоянной можно представить в следующем виде:

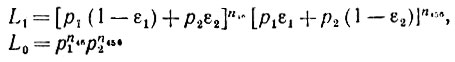(2.2.12)

при γ = 1 и 0 соответственно. Следовательно, для соответствующего отношения правдоподобия L₁/L₀ имеем

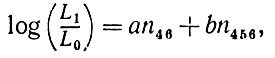(2.2.13)

где

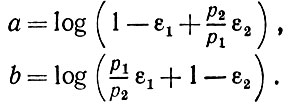(2.2.14)

Итак, алгоритм, основанный на критерии Неймана - Пирсона, позволяет распознать идеальный диффузный образ (γ = 0), если

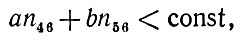(2.2.15)

и деформированный диффузный образ (γ = 1) в противном случае. Постоянную в правой части неравенства (2.2.15) следует выбирать таким образом, чтобы обеспечить желаемый уровень критерия. Сделать это можно с помощью метода, примененного в разд. 3.2 т. 1 в целях определения характеристик распределений для вероятностных автоматных языков, чем мы и займемся в оставшейся части данного раздела.

На самом деле мы можем упростить вывод благодаря тому обстоятельству, что здесь в отличие от ситуации разд. 3.2 т. 1 грамматика предполагается однозначной.

Для того чтобы изучить некоторые другие характеристики распределений автоматных языков, обратимся к числу N появлений цепочки состояния j₀, j₁,..,j_k в грамматически правильном предложении. Можно получить Е(N) для

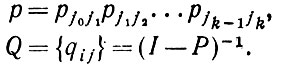(2.2.16)

В самом деле, справедлива следующая теорема.

Теорема 2.2.1.Математическое ожидание для указанного случая равно pq_1j0.

Доказательство. Определим индикаторную функцию как

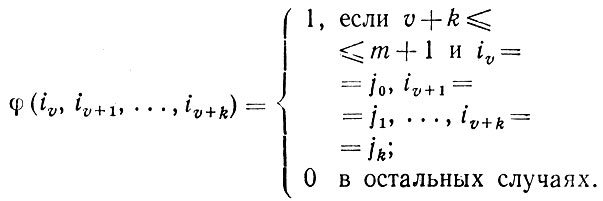92.2.17)

Число появлений цепочки j₀, j₁, ...., j_k в заданном предложении с состояниями i₀i₁... равно

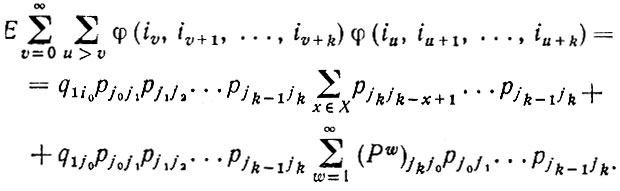(2.2.18)

Математическое ожидание числа появлений этой цепочки в заданном предложении равно

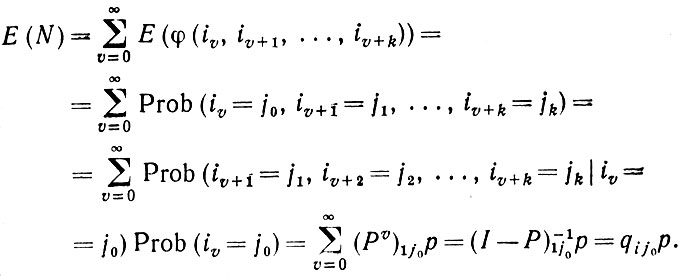(2.2.19)

Чтобы получить выражение для дисперсии в замкнутой форме, следует также учесть возможность частичного повторения j-цепочки, т. е. возникновения ситуации, когда для некоторого x 1 ≤ x ≤ k, j₀ = j_x, j₁ = j_x+1,...,j_k-x = j_k. Обозначим через X множество таких значений x и введем величину

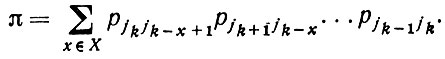(2.2.20)

Тогда имеет место следующая теорема:

Теорема 2.2.2. Дисперсия равна:

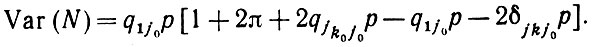(2.2.21)

Доказательство.

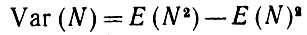(2.2.22)

и

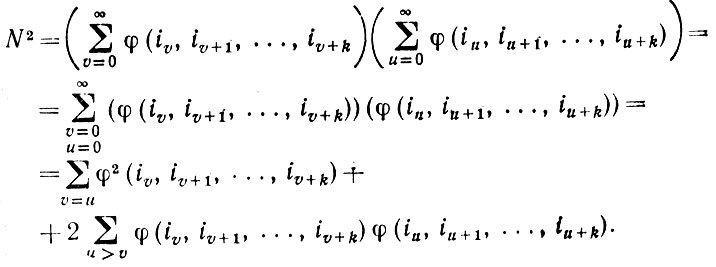(2.2.23)

Поскольку, однако, φ² ≡ φ, математическое ожидание первой суммы в последнем выражении равно Е(N) (см. уравнение (2.2.19)). С помощью этого же приема получаем также, что

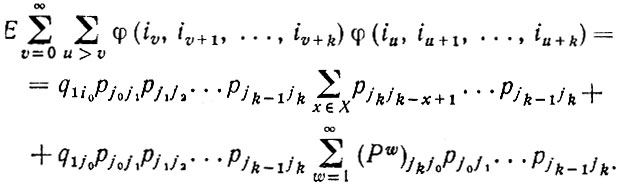(2.2.24)

Последнее выражение можно свести к следующему:

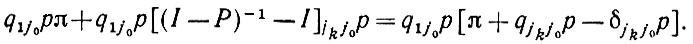(2.2.25)

Используя это выражение и учитывая значение Е(N), определенное предыдущей теоремой, приходим к утверждению доказываемой теоремы (2.2.21).

В частном случае, когда цепочка j₁, j₂, ....,j_k не содержит значения j₀, π = 0 и δ_jkj0 = 0, так что выражение (2.2.21) упрощается:

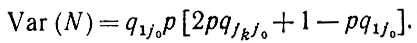(2.2.26)

С помощью этого же метода можно получить выражение в замкнутой форме для ковариации между N₁ и N₂, числами появления двух заданных j-цепочек. Последнее позволяет вычислить коэффициент корреляции между N₁ и N₂ -синтаксическую корреляцию двух стилистических приемов. Говоря о синтаксической зависимости, обычно мы имеем в виду ограничения регулярности, налагаемые грамматикой языка. Синтаксические же корреляции, с другой стороны, количественно характеризуют случайную взаимозависимость стилистических приемов, порожденную грамматикой употребления языка.