Глава 5. Образы-множества и статистическая геометрия

5.1. Единственные образующие

В данной главе образующие мы будем задавать в виде некоторых подмножеств опорного пространства X = R² и R³ с группами преобразований подобия EG (2) - EG (3) или TRANS (2) - TRANS (3). Примеры комбинаторных правил , подходящих для образов-множеств, можно найти в разд. 3.5, т. 1.

В большинстве разделов данной главы правило идентификации R мы будем выбирать так, чтобы идентификация множеств осуществлялась при помощи пересечений образующих или путем распространения этого принципа на логику признаков высшего порядка или другие логические функции.

Что касается деформаций, то мы рассмотрим несколько их типов. Первый ₁ - это выборочные деформации, введенные в случае 4.5.3 т. 1: n точек идеального изображения отбираются при помощи простой случайной выборки из равномерного распределения, заданного на I. Естественно, для того чтобы это имело смысл, необходимо выполнение условия 0 < m(I) << ∞, где m - лебегова мера. В качестве ошибки восстановления будем использовать площадь m(I^*ΔI) симметрической разности между идеальным и восстановленным изображениями I и I^* соответственно.

Второй механизм деформации ₂ был введен при рассмотрении случая 4.5.2 т. 1; деформированное изображение I состоит из точек, порожденных однородным пуассоновским процессом с постоянной интенсивностью λ (только в пределах I).

Третий механизм деформации ₃ представляет собой одну из разновидностей механизма случая 4.5.2 т. 1: здесь интенсивность пуассоновского потока равна λ₁ в пределах I и ₂ вне I. Для всех трех механизмов деформаций окно представляет собой дискретное множество точек, порожденных некоторым случайным, но зависящим от идеального изображения I способом.

После такого вступления мы готовы сформулировать задачу, которой будем заниматься в данной главе.

Статистическая геометрия: вывести образ по результатам наблюдения деформированного геометрического изображения I.

Существенным элементом этой задачи является не только восстановление идеального изображения, но, кроме этого, определение преобразований подобия в классе образов, порожденном некоторым прототипом, определение индексов класса образующих, входящих в соответствующие конфигурации, и множество иных задач. Чтобы восстанавливать изображение методом максимума правдоподобия, будем действовать следующим образом. Рассмотрим большую квадратную область Q = X₀⊂X и вычислим с помощью теоремы 1.2.1 производную Радона-Никодима

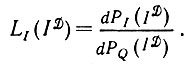(5.1.1)

При = ₁ приходим к элементарному соотношению

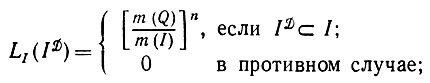(5.1.2)

так что восстановление по методу максимального правдоподобия оказывается эквивалентным решению уравнения

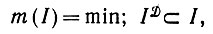(5.1.3)

т. е. мы ищем наименьшее идеальное изображение, содержащее деформированное.

Случай ₂ требует несколько больших усилий. Воспользуемся теоремой 1.2.1; см. также статью Гренандера (1950), с. 225. Покроем область Х₀ равномерной сетью квадратов и введем показатель, характеризующий число объектов, принадлежащих не пересекающимся подквадратам:

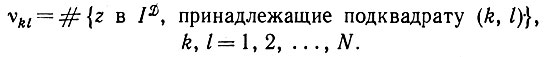(5.1.4)

Тогда при воздействии механизма деформации ₂ все случайные величины υ_kl независимы и характеризуются распределением Пуассона. Следовательно, мы получаем производную Радона-Никодима

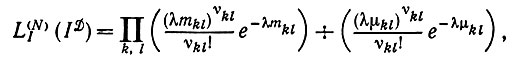(5.1.5)

где μ_kl - площадь m(X₀)/N² каждого подквадрата и m_kl - площадь пересечения подквадрата и идеального изображения I. Поэтому указанную производную можно записать в следующем виде:

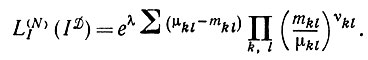(5.1.6)

При стремлении N к бесконечности все подквадраты станут пустыми, за исключением п подквадратов, соответствующих точкам, входящим в деформированное изображение I^D. Следовательно, предел выражения (5.1.6) дает производную Радона- Никодима

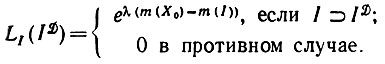(5.1.7)

Таким образом, восстановление по методу максимального правдоподобия все еще эквивалентно решению задачи минимизации (5.1.3).

И наконец, для случая ₃ мы с помощью аналогичных рассуждений получаем производную Радона-Никодима

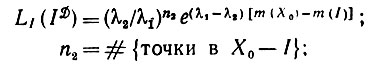(5.1.8)

в результате нам предстоит решить задачу отыскания максимума:

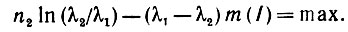(5.1.9)

Итак, нами доказана следующая теорема.

Теорема 5.1.1. При наличии механизмов деформации ₁, ₂ и ₃ восстановление по методу максимального правдоподобия обеспечивается решением уравнения (5.1.3) в случае и и уравнения (5.1.9) в случае ₃.

Отметим, что все эти деформации гетероморфные и деформированное изображение I^D количественно отличается от идеального I. Они, кроме того, ковариантны по вероятности.

Реализация соответствующих алгоритмов может оказаться неудобной в вычислительном отношении, и нам придется искать иные, более удобные методы. Все три механизма деформации вполне аналогичны друг другу, и ниже мы займемся первым из них.

Кроме этих трех механизмов деформации нам будет встречаться и четвертый ₄, когда мы будем заниматься множествами, идентифицируемыми с помощью правила R, представляющего пересечения объединений образующих. Другими словами, здесь мы работаем с логикой признаков множеств. Из указанных образующих случайно выбираются n, и результат идентифицируется снова с помощью пересечения. Эта процедура определяет деформированное изображение I^D, если установлен механизм случайного выбора.

Мы начнем анализ с простого случая - одноатомной конфигурации, т. е., конфигурации, включающей лишь одну образующую.

Пусть множество образующих G включает только диски g = (R, х₀, y₀)у где R - радиус и (x₀, y₀) - координаты центра диска. Всякому значению радиуса R соответствует класс образов, порожденный из прототипа (R, 0, 0).

Для того чтобы вывести образ при заданном центре, необходимо оценить всего один действительный параметр R. Если вернуться к восстановлению по методу максимального правдоподобия, то мы просто должны найти

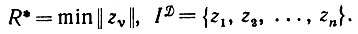(5.1.10)

Сейчас нас интересуют методы, которые можно было бы без соответствующих вычислительных затруднений распространить на менее тривиальные алгебры изображений, и в связи с этим обратимся к следующей альтернативе.

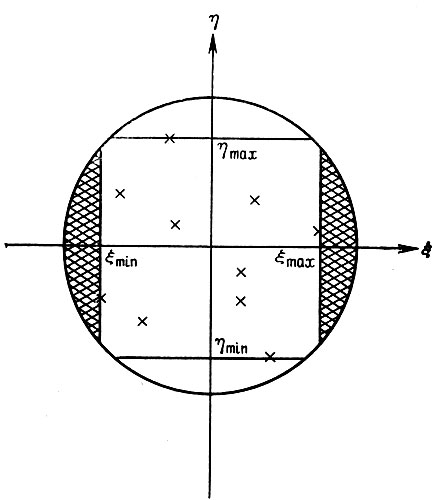
Рис. 5.1.1

Рассмотрим случай, представленный на рис. 5.1.1. В единичном круге С содержатся n точек, имеющих распределение, определяемое выборкой из равномерного распределения, заданного на C. Центр круга С расположен в начале координат, а упомянутые точки обозначены через z_υ = (ξ_υ, n_υ), υ = 1, 2, ..., n. Введем четыре случайные переменные:

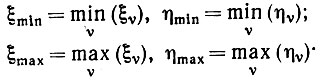(5.1.11)

Для начала мы хотели бы найти их функцию совместного распределения. Очевидно, что при увеличении n случайные переменные ξ_min и η_min будут стремиться к - 1, a ξ_max и η_max - к 1. Поэтому мы нормируем их так:

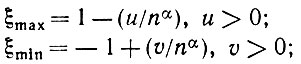(5.1.12)

конкретный вид нормировки, т. е. показатель степени а, будет определен позже. Переменные η_min и η_max будут подвергнуты аналогичным преобразованиям.

Рассмотрим функцию G от u и υ:

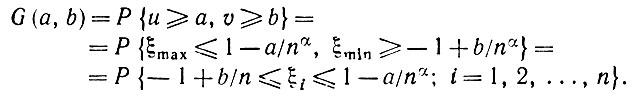(5.1.13)

Обозначим площадь правого заштрихованного сегмента на рис. 5.1.1 через A(d), причем ξ_max = 1 - d. Тогда

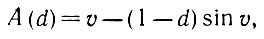(5.1.14)

где υ - половина центрального угла и, следовательно,

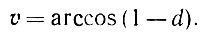(5.1.15)

Далее, учитывая оба заштрихованных сегмента, получаем, что

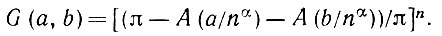(5.1.16)

Заметим, однако, что при малых значениях d из уравнения (5.1.15) асимптотически следует

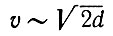(5.1.17)

и

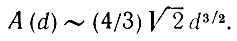(5.1.18)

Следовательно, выражение в (5.1.16), стоящее в квадратных скобках, включая множитель πⁿ, можно асимптотически представить как

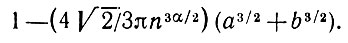(5.1.19)

Теперь из вида выражения (5.1.19) следует, что α = 2/3 -это то значение, которое обеспечит невырожденный предельный результат. Тогда получаем

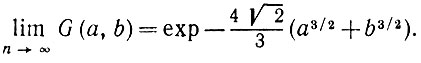(5.1.20)

Следовательно, случайные величины u и υ асимптотически независимы и характеризуются функцией распределения вейбулловского типа

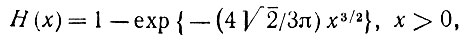(5.1.21)

и плотностью распределения вероятностей

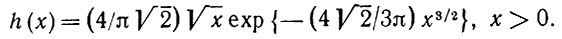(5.1.22)

Введем теперь эмпирический первый диаметр

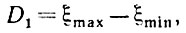(5.1.23)

распределение вероятностей которого явно инвариантно по отношению к переносам, и случайную переменную

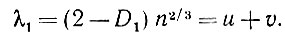(5.1.24)

Очевидно, что асимптотически случайная переменная λ₁ характеризуется плотностью распределения вероятностей h×h = k с соответствующей функцией распределения K = Н * Н, и потому результирующее распределение определяется выражением

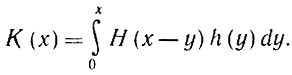(5.1.25)

Полученные результаты относятся к первому эмпирическому диаметру D₁ в направлении x. То же самое можно проделать и для второго эмпирического диаметра D₂ в направлении y, и нетрудно убедиться в том, что они асимптотически независимы. Эти результаты можно непосредственно обобщить на случай m диаметров с заданными различными направлениями φ₁, φ₂,...,φ_m.

Из этого следует, что при фиксированном m

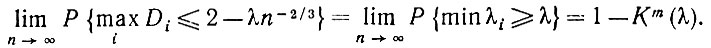(5.1.26)

Теперь мы перейдем к оценке неизвестного радиуса R круга по наблюдениям m эмпирических диаметров D₁, D₂,...,D_m. Эмпирические диаметры D_i обладают тем же асимптотическим распределением, что и выше, но с измененным масштабом в отношении 1:R; поэтому можно обратиться к выражению (5.1.25), чтобы получить статистическую оценку R^*, которая является асимптотически несмещенной оценкой медианы.

Итак, нами доказана следующая теорема.

Теорема 5.1.2. Статистическая оценка, получаемая по m диаметрам:

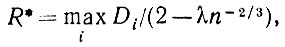(5.1.27)

является асимптотически несмещенной оценкой медианы, если X выбирается так, что оно удовлетворяет уравнению

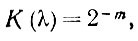(5.1.28)

причем доверительный интервал -

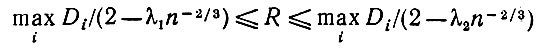(5.1.29)

и доверительный уровень -

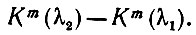(5.1.30)

Необходимо сделать одну оговорку относительно интерпретации и применения этой теоремы. Заманчиво выбирать m большим: если получать оценку R по большому числу диаметров, то, вероятно, она будет более эффективной. Это действительно так, но следует учитывать то обстоятельство, что при получении асимптотического результата мы пользовались малой вероятностью перекрытия соответствующих сегментов при больших выборках. Для любого значения m перекрытие можно исключить, если n → ∞. Если же одновременно увеличивать m, то данное утверждение, а следовательно, и соответствующие результаты (5.1.27) и (5.1.30) перестают быть справедливыми. В связи с этим для m следует выбирать скорее небольшие значения, скажем 4 или 6, если n имеет порядок 50-100.

Нам уже известно, что размер множества дрейфа может уменьшаться (см. теорему 4.5.5, т. 1). Теперь перейдем ко второму этапу идентификации изображения / и попытаемся оценить

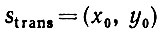(5.1.31)

с помощью оценок x^*₀, y^*₀, базирующихся на m диаметрах множества Φ_m направлений φ.

Обозначим через ξ^φ_max и ξ^φ_min минимум и максимум соответственно, измеренные по направлению φ. Используя те же, что и выше, обозначения, получаем

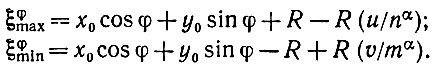(5.1.32)

В данном случае мы воспользуемся их средним:

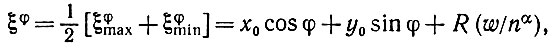(5.1.33)

где w = υ - u. Из предыдущего известно, что для всякого множества Φ m значений

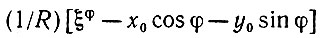(5.1.34)

асимптотически независимы, причем каждое из них характеризуется функцией распределения

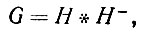(5.1.35)

где Н^- обозначает функцию распределения - u. Отметим, что G является симметризацией Н и потому G = 1/2 - нечетная функция. Математическое ожидание w, разумеется, равно нулю, а дисперсия 2σ².

Для идентификации х₀ (и аналогично y₀) воспользуемся линейной комбинацией средних значений ξ^φ:

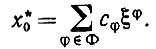(5.1.36)

Согласно требованию не смещенности,

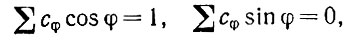(5.1.37)

в то время как дисперсия большой выборки равна

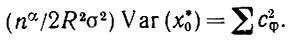(5.1.38)

Допустим, что m направлений размещены равномерно:

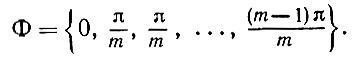(5.1.39)

Учитывая, что α = 2/3, получаем

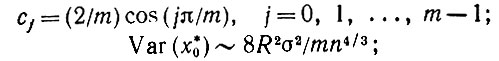(5.1.40)

эти соотношения можно использовать для определения доверительных интервалов для х₀ и y₀.

Выражения (5.1.40) заслуживают нескольких дополнительных замечаний. Замена деформированного изображения I^D признаками R^*₁, x^*₀ и y^*₀ была осуществлена с помощью граничных признаков деформированного изображения I^D - величин, полученных на основе ξ^φ_max и ξ^φ_min, и их линейной комбинации. Мы воспользовались квазилинейной процедурой выделения признаков.

Если бы вместо этого мы воспользовались линейными признаками 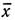, ȳ, т. е. координатами центра тяжести деформированного изображения I^D, то дисперсия была бы порядка n^-1. Отдав предпочтение квазилинейным граничным признакам, мы добились увеличения точности восстановления на величину порядка n^1/3.

Если бы мы применяли теорему 5.1.1 непосредственно к g - произвольному кругу, то пришлось бы отыскивать круг наименьшего радиуса g_min, содержащий множество точек I^D = {z₁, z₂, .. ., z_n}. Полный перебор в этом случае практически невозможен, за исключением вариантов с очень малыми значениями n. В самом деле, круг g_min должен проходить по меньшей мере через две точки I^D, и если это число точек действительно равно двум, то это противоположные точки диаметра g_min В связи с этим необходимо просчитать C²_n кругов. Если, с другой стороны, круг проходит по меньшей мере через три точки I^D, что определяет R, х₀ и y₀,то необходимо просчитывать С³_n кругов, проверяя для каждого круга, покрывает ли он I^D и выбирая наименьший из таких кругов.

В статье Басса и Шуберта (1967) предложен более удачный алгоритм, в основе которого лежат следующие соображения. Если диаметр равен d, то радиус g_min снизу ограничен величиной d/2, а сверху d/√3. Первое очевидно. Докажем второе. Пусть g - круг радиуса r, в который вписан равносторонний треугольник со стороной d. В таком случае r = d/√3, где d - диаметр множества вершин треугольника. Рассмотрим теперь некоторое другое множество диаметра d', включающее три другие точки на dg, которые не образуют равносторонний треугольник. В таком случае r = d/√3 < d'/√ 3, что и требовалось доказать.

Алгоритм. Шаг 1. Формируем выпуклую оболочку деформированного изображения H = conv(I^D) и множество его экстремальных точек Е; эффективная процедура для выполнения этого шага приведена в следующем разделе.

Шаг 2. Определяем диаметр Н путем вычисления расстояний между всеми парами точек Е и выбора наибольшего из них.

Шаг 3. Проверяем, покрывает ли круг с этим диаметром (возможно, несколько кругов) деформированное изображение I^D. Если да, то работа алгоритма закончена.

Шаг 4. В противном случае формируются круги g, проходящие через три экстремальные точки Е. Круги, для которых выполняется неравенство d/2 < R < d/√3, при увеличении R, подвергаются проверке: покрывают ли они I^D из тех, которые покрывают, выбирается круг с наименьшим R.

Данный алгоритм представляет собой явное улучшение по сравнению с "лобовым" алгоритмом, но тем не менее необходимые затраты машинного времени при больших значениях n будут ощутимыми. Более совершенный алгоритм описан в работе Шамоса (1975).

Случай, когда алгебра изображений 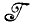включает только круги, является, конечно, очень частным. Давайте поэтому обратимся к случаю, когда класс образов порождается для всех sV, причем прототип V представляет собой некоторую замкнутую выпуклую фигуру непрерывной кривизны. Если бы мы допустили существование углов, то описываемый ниже анализ пришлось бы модифицировать, но обсуждение того, как это сделать, мы пока отложим. Начнем со случая, когда S - изменения масштаба, и следовательно, требуется идентифицировать коэффициент изменении масштаба, скажем R. Пусть площадь V равна А.

Рассмотрим рис. 5.1.2, где Т₁ и Т₂ - две опорные прямые с направлением φ. Обозначим радиусы кривизны в точках касания Р₁ и Р₂ через R₁(φ) и R₂(φ) соответственно. Введем координатную ось ξ перпендикулярную направлению φ.

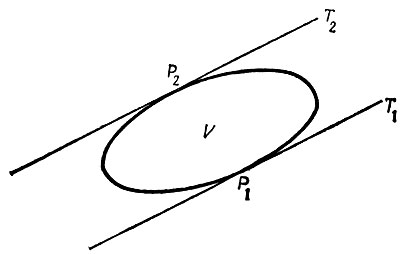
Рис. 5.1.2

Для деформированного изображения введем показатели ξ^φ_min и ξ^φ_max аналогичные величинам, введенным при рассмотрении круга (см. рис. 5.1.1). Тогда можно записать

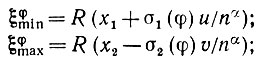(5.1.41)

где коэффициенты σ_i(φ) характеризуют размер малого сегмента в точках касания P_i, т. е.

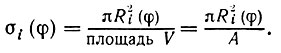(5.1.42)

Величину

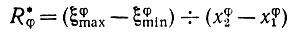(5.1.43)

можно представить как

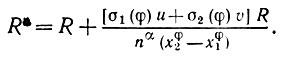(5.1.44)

Объединяя m таких значений в некоторый новый признак

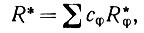(5.1.45)

выбираем коэффициенты c_φ так, чтобы выполнялось

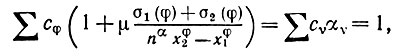(6.1.46)

где μ -математическое ожидание распределения Н и

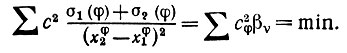(5.1.47)

(Смысл α_υ и β_υ здесь очевиден.) Отсюда непосредственно получаем, что

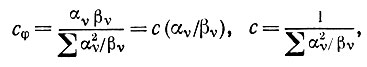(5.1.48)

а дисперсия нового признака равна в результате

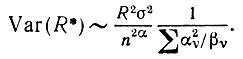(5.1.49)

При рассмотрении круга не возникала задача, которая встает для данного прототипа V, когда преобразования подобия S - группа вращений. Пусть масштаб и положение идеального изображения I определены (мы будем пользоваться обозначениями, введенными в связи с рис. 5.1.2). Неизвестный угол поворота обозначим через 0. В таком случае все 2m значений множества

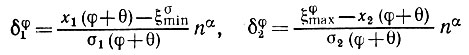(5.1.50)

асимптотически независимы и характеризуются распределением Н с математическим ожиданием μ. Поэтому естественно оценивать θ путем решения задачи наименьших квадратов:

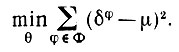(5.1.51)

Это нелинейная задача наименьших квадратов, но для получения асимптотического решения достаточно линеаризовать функции от θ, входящие в выражения для δ^φ_i. Здесь предполагается, что 2m значений x_i(φ + θ) однозначно определяют угол θ.

Теперь можно перейти к более богатой алгебре изображений . Пусть прототипом снова служит единичный диск, а преобразования подобия S = {переносы, изменения масштаба}. Если правило R идентифицирует объединения образующих V, то получатся изображения, подобные приведенному на рис. 5.1.3, а. Если для любого изображения допускаются только два прототипа, то возникает шести мерная алгебра изображений: четыре измерения для центров и два-для радиусов. Специализированная процедура идентификации, основанная на использовании центра тяжести и моментов инерции, в данном случае работать не будет.

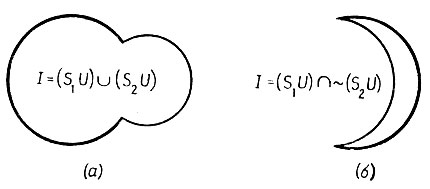
Рис. 5.1.3

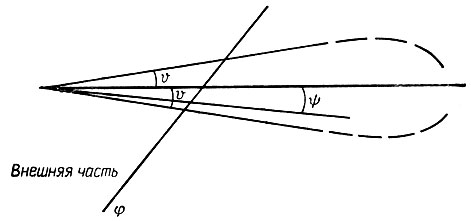
Рис. 5.1.4

Можно, однако, положить в основу идентификации статистики граничных значений, распространив на данный случай уже применявшийся нами подход. Эта методология применима, если принять во внимание частный случай, возникающий при приближении к I по одной из двух общих для обоих кругов касательных. Сделав это, мы получим вместо одного два вклада в распределение показателей ^φ_max и ξ_min две точки соприкосновения касательной с I.

Если же вместо этого правило R идентифицирует пересечения образующих и их дополнений, то получатся серповидные изображения типа приведенного на рис. 5.1.3, б. В данном случае нашу методологию следует расширить так, чтобы она позволяла работать с изображениями, в которых присутствуют углы.

Рассмотрим в связи с этим вершину, представленную на рис. 5.1.4 и имеющую центральный угол 2.υ Теперь мы приближаемся к I^D⊂I по направлению φ, которое здесь удобнее задать углом - ψ (см. рис. 5.1.4). Обозначив полную площадь I через А = m(I), получаем для вероятности попадания точки, выбранной в I случайным образом, в область, расположенную слева от φ, следующее выражение:

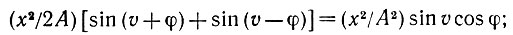(4.1.52)

это выражение справедливо асимптотически для небольших значений x при условии непрерывной кривизны вне вершины. Теперь становится ясно, как следует нормировать x. Пусть

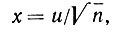(4.1.53)

что приводит к следующей асимптотической функции распределения для u:

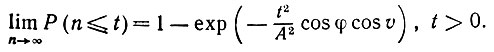(5.1.54)

Такое полу нормальное распределение можно использовать для обработки изображений с углами вместо H - распределения, которое годится для случая гладких границ. Более подробно с возможностями использования точек разрыва на границах можно познакомиться по статье Гренандера (1973а), с. 842-846.

При переходе к более богатым алгебрам изображений, сформированным аналогично при больших dim(F), можно в принципе применять этот же метод. Для алгебр изображений высших размерностей это, однако, уже не кажется столь же естественным, и потому предпочтение отдается более непараметрическим методам. Что касается практики, то уже при шести мерных серповидных изображениях может возникнуть такая ситуация. Рассмотрим несколько альтернативных процедур идентификации.

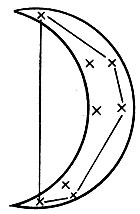
Рис. 5.1.5

Начнем с алгебры F = {серповидные изображения}. Сформируем выпуклую оболочку (см. рис. 5.1.5) и обозначим длины сторон через и их ориентации через α_i. Рассмотрим концевые точки Р' и Р" стороны с наибольшей длиной и введем круги С(Р', Р", ρ) радиуса ρ, проходящие через точки Р' и Р".

Построим изображение вида

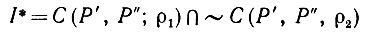(5.1.55)

и выбираем ρ₁ и ρ₂ так, чтобы обеспечить m(I^*) = min с учетом ограничения I^*⊂I. Можно доказать, что это состоятельная оценка идеального изображения I.

Еще одна статистика граничного показателя, которую можно было бы использовать,- это множество значений

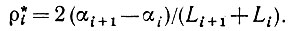(5.1.56)

Это оценки кривизны, и их можно использовать как для оценивания обратных величин l/R и l/R₂, так и для определения положения центров обоих кругов.

Анализ, изложенный в данном разделе, базируется в основном на статистиках граничных показателей. Строго говоря, I^D не имеет нетривиальной границы, так как оно является просто дискретным точечным множеством. Мы ввели функции от деформированного изображения I^D, они аппроксимируют соответствующие функции от I. Эти функции представляют свойства границы ∂I или производных величин типа диаметров.

Рассмотренные статистики граничных показателей ковариантны по вероятности (см. разд. 1.2) и легко поддаются вычислению. Так, например, для определения ξ_min в (5.1.11) достаточно найти точку с минимальным значением координаты x. Это можно

сделать с помощью всего лишь n - 1 сравнения. Восстановление по методу максимального правдоподобия, которое с теоретической точки зрения выглядит предпочтительнее, в общем случае оказывается менее привлекательным в вычислительном смысле.

Естественным продолжением изложенного является переход к алгебрам изображений с более чем одним прототипом, например кругами и квадратами. При этом статистики граничных показателей будут, судя по всему, естественным инструментом, однако этот вопрос еще не изучен.