5.2. Выпуклые множества - логика признаков первого порядка

Алгебры изображений, рассматривавшиеся в предыдущем разделе, весьма жесткие: их можно параметризовать с помощью нескольких действительных параметров. Теперь мы переходим к более "свободным" алгебрам изображений, т. е. допускаем изображения с произвольной, даже бесконечной числовой сложностью (см. т. 1, с. 249). В данном разделе структурная сложность логики признаков равна единице, в разд. 5.3 она равна двум, а в разд. 5.4 -бесконечности; соответствующие множества предполагаются компактными.

Пусть в роли образующих выступают полуплоскости, а правило идентификации определяет пересечение образующих, так что мы приходим к идеальным изображениям, представляющим собой выпуклые множества на плоскости. Как же следует восстанавливать идеальное изображение, если = ₁?

Совершенно очевидно, что утверждение, лежащее в основе соотношения (5.1.3), обеспечивает восстановление по принципу максимального правдоподобия выпуклой оболочки деформированного изображения I^D:

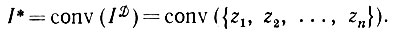(5.2.1)

Разумеется, I^* будет стремиться к идеальному изображению I в том смысле, что

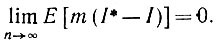(5.2.2)

Доказательство соотношения (5.2.2) мы предоставляем выполнить читателю. Прежде чем перейти к обсуждению критической проблемы скорости сходимости в (5.2.2), остановимся кратко на алгоритмических аспектах вычисления I^*.

"Наивный" (и расточительный) алгоритм выглядит так:

Шаг 1. Приближаемся к I^D полуплоскостями снизу так, чтобы эти полуплоскости были ограничены горизонтальными прямыми. Выбирается первая встреченная точка I^D. На рис. 5.2.1 а - это точка P₁. Если встречается не одна точка, то выбираем самую левую из них. Этот шаг связан с вычислением min y_i после чего, возможно, потребуется определить минимальное значение x_i.

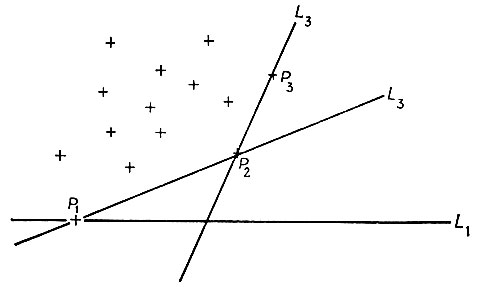
Рис. 5.2.1 а

Шаг 2. После того как точки P₁, Р₂,...., P_k определены, вычисляем углы между

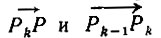
для всех точек Р в I^D, для которых еще не установлена принадлежность границе conv(I^D), за исключением P₁. Для этого необходимо многократное вычисление арктангенса. Выбираем точку Р, для которой указанный угол наименьший, или, если такая точка не единственная, выбираем ту точку на данном направлении, которая расположена на наибольшем расстоянии от P_k. На рисунке, где k = 2, мы имеем

Шаг 3. Возвращаемся к шагу 2 до тех пор, пока опять не встретится точка Р₁.

Сколько раз необходимо вычислять арктангенс в этом алгоритме, не зависит от количества экстремальных точек в деформированном изображении I^D. На самом деле нам, конечно, не нужна собственно величина угла - требуется лишь некоторая монотонная функция от*него; поэтому от вычисления арктангенса можно отказаться, заменив его вычислением Δy/Δx. Если I имеет гладкую границу, то можно ожидать, что I^* содержит порядка n^1/3 экстремальных точек (см. примечания), и потому можно рассчитывать на то, что потребуется вычислить порядка n^4/3 значений. К этой величине следует добавить объем вычислений, необходимых для отыскания наименьшего угла в процессе каждого исполнения шага 2.

Довольно очевидно, что данный алгоритм слишком неэффективен для использования в случае любых, кроме небольших, значений n. В литературе можно встретить ряд попыток увеличить скорость за счет лучшей конструкции алгоритма, и мы рассмотрим алгоритм, предложенный Грэхемом (1972).

Шаг 1. В пространстве R² отыскиваем некоторую точку Р, принадлежащую внутренности conv(I^D), например, путем проверки на коллинеарность трех точек вплоть до получения отрицательного результата; далее используем точку, расположенную внутри треугольника, построенного на этих трех точках. Если P - одна из точек z_k, то эта точка z_k исключается.

Шаг 2. Определяем полярные координаты точек z_k = (r_kφ_k) деформированного изображения I^D относительно точки Р и некоторого фиксированного направления. Для этого необходимо а раз вычислить арктангенс (см. замечание по этому поводу, сделанное выше), а также выполнить возведения в квадрат, сложения и извлечения корня, необходимые для определения радиусов.

Шаг 3. Элементы z_k упорядочиваем по возрастанию φ_k. Для этого требуется порядка (n log n) операций (см., например, т. 3 монографии Кнута (1973)).

Шаг 4. Если φ_k = _k+1 удаляем точки P_k и P_k+1 для которых радиус наименьший.

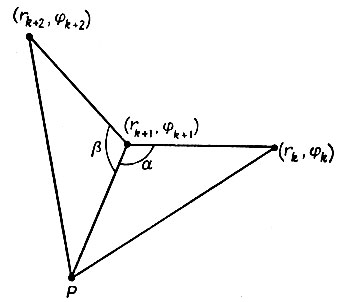
Рис. 5.2.1 б

Шаг 5. См. рис. 5.2.16. Вычисляем угол γ = α + β, причем вначале рассматриваем три последовательные точки:

(а) если α + β ≥ π, то среднюю точку исключаем;

(б) если α + β ≤ π, то возвращаемся к шагу 5, но при этом добавляем следующую точку.

На шаге 5 мы либо уменьшаем временно множество точек, входящих в conv(I^D), на единицу, либо увеличиваем на единицу общее число точек, которые в данный момент служат объектом анализа. Итак, алгоритм закончит работу самое "большее за 2n итераций.

Для оценки качества работы этого алгоритма необходимо знать время работы центрального процессора ЭВМ, потребное для выполнения операций алгоритма, например, соотношение числа арифметических операций и сравнений. Чему бы ни было равно это соотношение, при очень больших значениях n основная составляющая общей потребности в машинном времени будет пропорциональна n log n. Следовательно, этот алгоритм работает лучше, чем "наивный", и позволяет определять conv(I^D) даже при очень больших значениях n.

Однако скорость вычислений - это только одна из сторон проблемы. Необходимо оценить также скорость сходимости в (5.2.2), что существенно сложнее. Известно два результата: один из них относится к ₁ и другой - к ₄. Их доказательство требует довольно подробного анализа, такого, который, вероятно, в будущем часто будет применяться в статистической геометрии.

Первый и весьма элегантный результат принадлежит Реньи и Сьюланке (1964); заключается он в следующем.

Теорема 5.2.1.Пусть I - ограниченное выпуклое множество, граница которого имеет достаточное число производных с положительной кривизной k = k(s), где s-длина дуги. Тогда

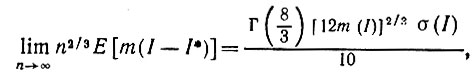(5.2.3)

где σ(I) определено в (5.2.33).

Доказательство. Пусть ε_ij = 1, если i ≠ j и 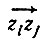принадлежит границе ∂I^*, и пусть F_n = m(I^*). Тогда, если p(z_i, z_j) - расстояние от начала координат, выбранного, скажем, внутри I, то можно записать, что

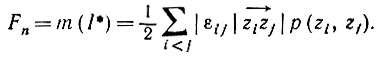(5.2.4)

Взяв математическое ожидание от этой величины, получаем следующее:

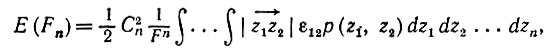(5.2.5)

где dz_i - мера Лебега. Интегрирование (5.2.5) по z₃, z₄, ...., z_n приводит к

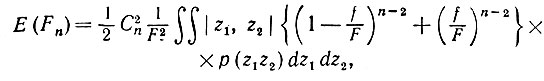(5.2.6)

где f - наименьшая площадь, отсекаемая от 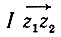(см. рис. 5.2.2а). Естественно, f ≤ F/2, и потому вторым членом подынтегрального выражения можно пренебречь. Следовательно,

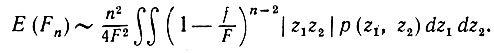(5.2.7)

Для того чтобы преобразовать это выражение, обратимся к одному классическому результату из интегральной геометрии (см. Бляшке (1949) с. 16):

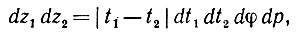(5.2.8)

где p -расстояние от прямой 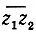до начала координат, φ - угол, образуемый этой прямой с некоторым фиксированным направлением, и t₁ и t₂ - параметры точек z₁ и z₂ этой прямой. Но

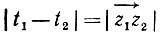
и

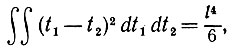(5.2.9)

где l = l(р, φ) - длина хорды, образованной пересечением l с z₁z₂. Подставляя в (5.2.7) выражения (5.2.8) и (5.2.9), получаем

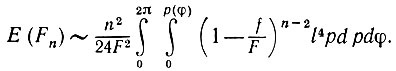(5.2.10)

Основной вклад в правую часть выражения (5.2.10) определяется, несомненно, той частью области интегрирования, где f мала. Для определения этого вклада аппроксимируем ∂I ее соприкасающимися окружностями и определим ошибку аппроксимации (соответствующие обозначения проиллюстрированы на рис. 5.2.26). Для обозначения приближенных величин будем использовать черту над буквой, например 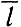вместо l.

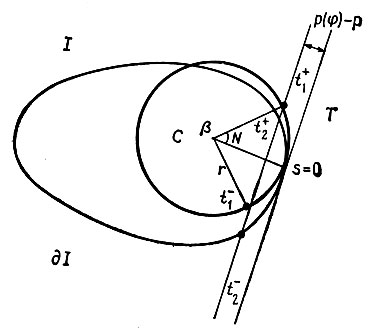
Рис. 5.2.2 б

Введем параметр β, равный половине центрального угла в центре С соприкасающейся окружности O_φ, построенной на хорде (β, φ) так, что

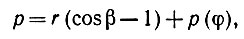(5.2.11)

где r = 1/k -радиус кривизны, k - кривизна. Воспользуемся длиной как параметром на прямой (p, φ), точки пересечения которой с окружностью O обозначены через t⁺₁ и t^-₁ и с границей ∂I - через t⁺₂ и t^-₂. При надлежащем выборе t = 0 получаем, что

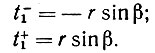
Пусть теперь z(s) -некоторая точка I, s -длина дуги и при s = 0, T - единичный вектор касательной, а N - единичный нормальный вектор. Тогда можно разложить

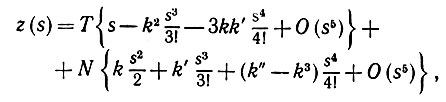(5.2.13)

используя формулы Френе. Хорда (β, φ), однако, определяется уравнением откуда следует, что

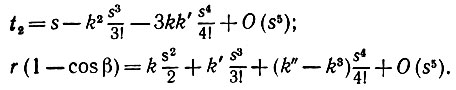(5.2.15)

Из второго уравнения следует, что

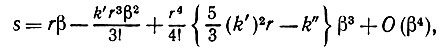(5.2.16)

а первое тогда превращается в следующее:

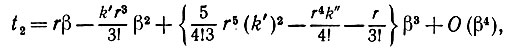(5.2.17)

где t^-₂ = t₂(-β) и t⁺₂ = (β). Учитывая этот результат и разлагая синусоидальную функцию в (5.2.12), получаем

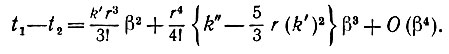(5.2.18)

Если k' ≠ 0, как это имеет место на нашем рисунке, то соприкасающаяся окружность О_φ пересекает ∂I, и, следовательно,

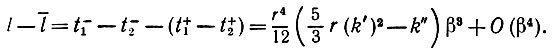(5.2.19)

Если же k' = 0, то уравнение (5.2.19) справедливо тем более, поскольку порядок касания равен трем или большей величине. И наконец, ошибка аппроксимации площадей равна

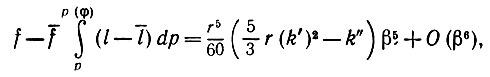(5.2.20)

и теперь можно вернуться к уравнению (5.2.10). При этом мы будем отталкиваться от центрального угла α = 2β, так что

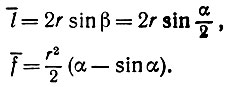(5.2.21)

Кроме того,

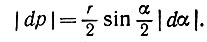(5.2.22)

В сочетании с (5.2.19) это приводит к следующему:

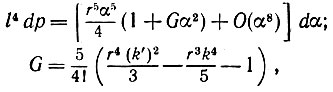(5.2.23)

и аналогично

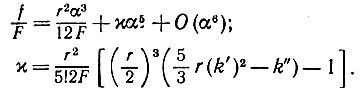(5.2.24)

При этом интеграл (5.2.7) принимает вид

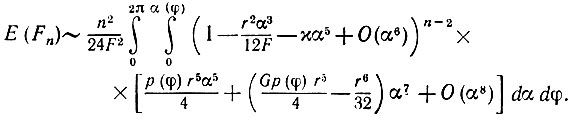(5.2.25)

Теперь нам нужен интеграл

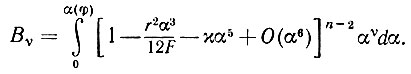(5.2.26)

Подставим

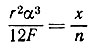(5.2.27)

и воспользуемся тем, что

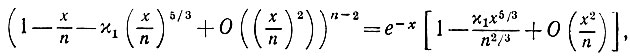(5.2.28)

где χ₁ = χ(12F/r²)^5/3. Следовательно,

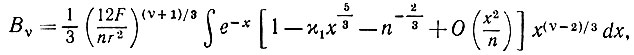(5.2.29)

причем интегрирование ведется в диапазоне от нуля до nr²α³(φ)/12F. Если же мы, однако, будем интегрировать вплоть до +∞, то возникает ошибка экспоненциального порядка, которой можно пренебречь. Итак,

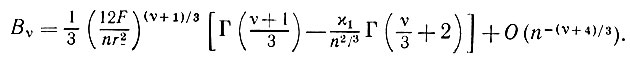(5.2.30)

Подставляя (5.2.30) в (5.2.25), получаем, наконец, что

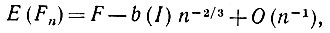(5.2.31)

где

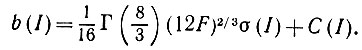(5.2.32)

При этом

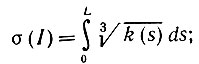
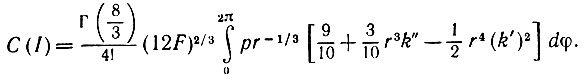(5.2.33)

Выражая последнее соотношение через производные по φ (они обозначены точками), получаем

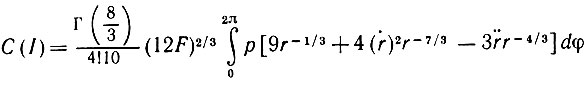(5.2.34)

или, дважды интегрируя по частям и используя соотношение 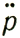+ p = r, (см. т. 1, с. 156) получаем

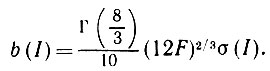(5.2.35)

На этом доказательство теоремы заканчивается.

Второй результат, относящийся к скорости сходимости I^* к I при n → +∞, связан с применением ₄. Выбор из ряда полуплоскостей именно тех, пересечение которых образует I, производится следующим образом. Вдоль границы ∂I случайным образом выбираем п точек с равномерным распределением относительно длины дуги. Пересечение соответствующих опорных полуплоскостей I в этих точках и составит I^D.

Чтобы получить I^*, восстановленное по принципу максимального правдоподобия, отметим, что увеличить правдоподобие можно не только как плотность распределения, но и как дискретную вероятность, допустив касание I^* со всеми полуплоскостями № вдоль n сегментов положительной длины, скажем l₁, l₂,...,l_n. Естественно, здесь l_i ≤ L_i, где L_i - длина границы I^D. Тогда правдоподобие будет пропорционально произведению l₁l₂...l_n и его можно максимизировать, выбирая l_i = L_i, для всех i, что эквивалентно выбору I^* = I^D.

Теперь возникает одна дополнительная трудность, заключающаяся в том, что, строго говоря, величина m(I^* - I) не имеет конечного математического ожидания. Напомним, что I⊂I^* для ₄ и что I^* может не быть ограниченной, как это показано на рис. 5.2.3в. Это происходит с вероятностью, стремящейся к нулю при больших n, но при всех конечных значениях n эта вероятность положительна и, следовательно, m (I^*) = +∞. Для того чтобы преодолеть это затруднение, величину m(I^* - I) разбиваем на две части, вторая из которых имеет бесконечное математическое ожидание, но тем не менее мала; в точном виде этот факт сформулирован в следующей теореме (Карлссон и Гренандер (1967)), которая охватывает несколько более общий случай - n точек необязательно выбирать из равномерного распределения на длинах дуг

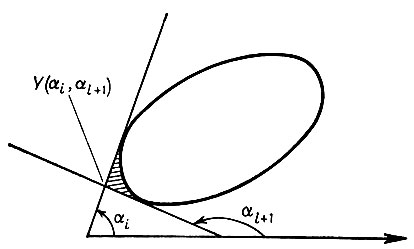
Рис. 5.2.3 а

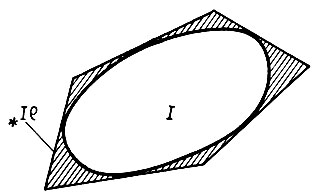
Рис. 5.2.3 б

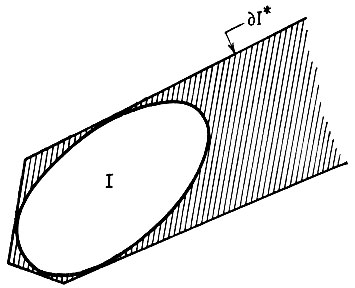
Рис. 5.2.3 в

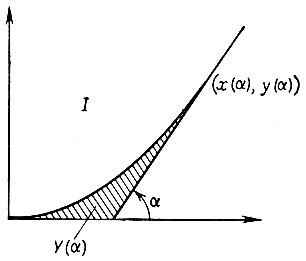
Рис. 5.2.3 г.

Теорема 5.2.2.Пусть I - ограниченное выпуклое множество с достаточно гладкой границей (x(α), y(α)), где α - угол касательной. Кривизна должна быть положительной. Выборочные точки α₁ < ₂ <...< α_n из интервала (0,2π) характеризуются положительной плотностью вероятностей р(α) из C₁ и определяют пересечение с I^* соответствующих полуплоскостей. Тогда нормированную ошибку восстановления n²m(I^* - I) можно представить в виде суммы двух членов X_n (см. (5.2.43)) и ε_n, таких, что

(5.2.36)

и ε_n → 0 по вероятности при n → ∞. Более того, вся нормированная ошибка восстановления в целом стремится по вероятности к величине (5.2.36).

Доказательство. Можно записать, что

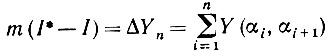(5.2.37)

(соответствующие обозначения приведены на рис. 5.2.3а); мы положили здесь α_n+1 = α_i. Чтобы изучить поведение множества вида Y(α_i, α_i+1), рассмотрим рис. 5.2.3г. Здесь начало координат помещается в точке α_i ось x совпадает с касательной в этой тоже и α_i+1 - α_i = α.

Рассмотрим площадь области Y(α), расположенной под кривой (x(β), y(β)), 0 ≤ β < α, и обозначим радиус кривизны при β через R(β) (что соответствует углу α_i + β). В результате с помощью элементарных вычислений получаем, что

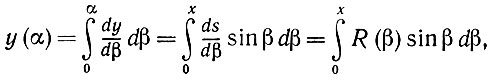(5.2.38)

и, следовательно,

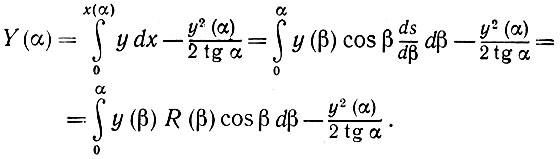(5.2.39)

Далее, объединив (5.2.38) и (5.2.39), можно при малых а получить следующее разложение:

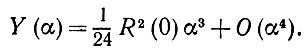(5.2.40)

Отсюда следует, что

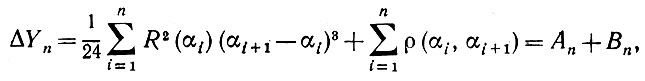(5.2.41)

где

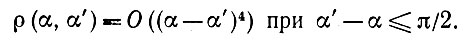(5.2.42)

Покажем, что второй член B_n в (5.2.41) является асимптотически пренебрежимо малым.

Введем

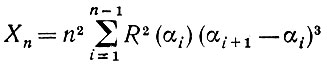(5.2.43)

и, обратив внимание на то, что верхний предел суммирования равен n - 1, а не n, вычислим математическое ожидание этой величины. Для нашей упорядоченной выборки значений а приходим к обычному выражению для порядковых статистик

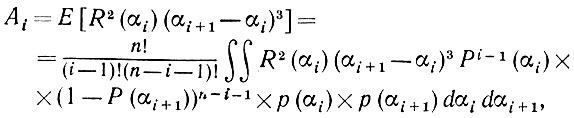(5.2.44)

где интегрирование ведется в диапазоне 0 ≤ α_i < α_i+1 ≤2π и Р - функция распределения, соответствующая плотности распределения р. Воспользуемся подстановкой

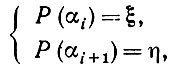(5.2.45)

которая является взаимно однозначной, поскольку функция распределения Р - строго возрастающая. Тогда имеем

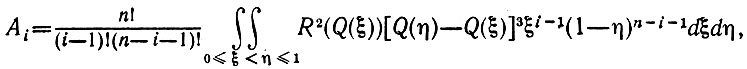(5.2.46)

где Q - это обратная функция P^-1. Объединим последнее выражение с (5.2.43):

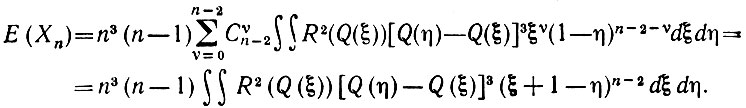(5.2.47)

Воспользуемся подстановкой

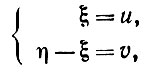(5.2.48)

так что

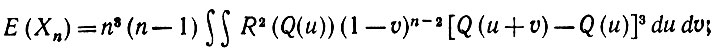(5.2.49)

здесь интегрирование ведется по области u, υ ≥ 0 и u + υ ≤ 1. Разложим функцию Q(u + υ) в ряд Тейлора в окрестности u. Но так как

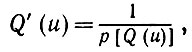
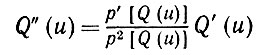(5.2.50)

ограниченны и непрерывны, то

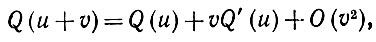(5.2.51)

откуда следует, что

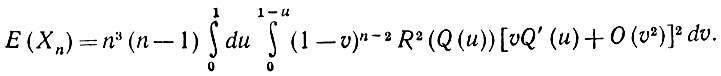(5.2.52)

Проинтегрируем выражение (5.2.52) сначала по υ:

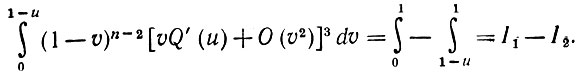
Но поскольку

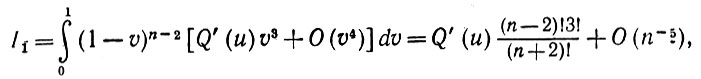(5.2.53)

a I₂ ограничено постоянными значениями времени, то

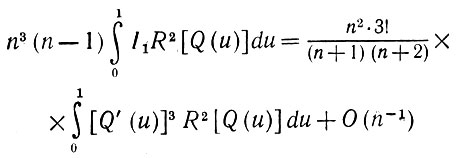(5.2.54)

Проинтегрируем теперь выражение (5.2.52) по u. В результате получаем

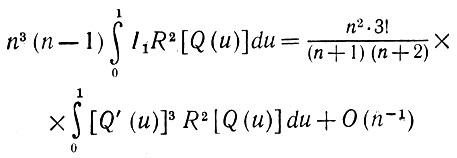(5.2.55)

и

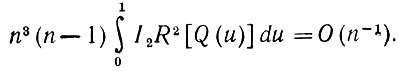
Следовательно,

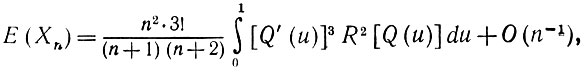(5.2.57)

или, сделав обратные замены переменных,

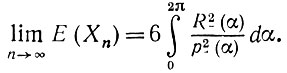(5.2.58)

Остается рассмотреть член

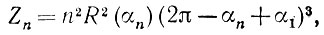(5.2.59)

так как, определяя X_n с помощью (5.2.43), мы его не учитывали. Это не вызывает затруднений, поскольку

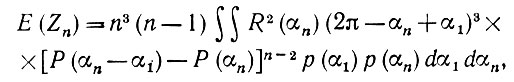(5.2.60)

где интегрирование ведется по 0 ≤ α₁ < α_n ≤ 2π можно воспользоваться подстановкой

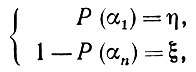(5.2.61)

что приводит к следующему:

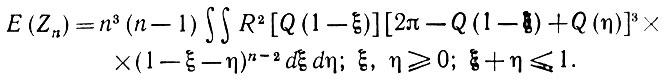(5.2.62)

Выражение (5.2.62) можно мажорировать постоянными значениями времени:

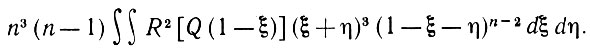(5.2.63)

Вид последнего выражения аналогичен (5.2.56), и, следовательно, Е (Z_n) → 0. На этом заканчивается первая часть доказательства*

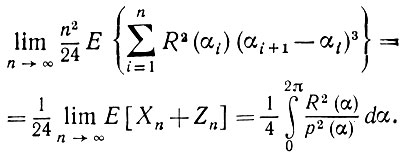(5.2.64)

На следующем шаге предстоит усилить утверждение (5.2.64), показав, что не только математическое ожидание сходится, но и сама величина стремится по вероятности к этому пределу. Чтобы сделать это, допустим, что (β',β") - малый интервал в интервале (0, 1), и рассмотрим выражение

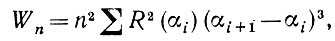(5.2.65)

где суммирование ведется по P(α_i)∈(β' - β"), или выражение

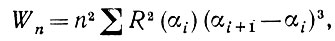(5.2.66)

где _i = Р (α_i) (β' - β"). Если разность β" - β' достаточно мала и n , достаточно велико, то при любом δ > 0 величину W_n можно заключить между двумя предельными значениями:

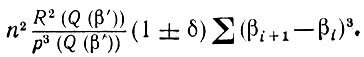(5.2.67)

Используя традиционное представление упорядоченной равномерной выборки в виде

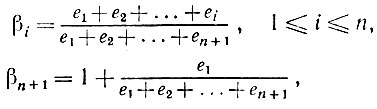(5.2.68)

где E_I - тождественно независимо распределенные наблюдения, подчиняющиеся экспоненциальному распределению, можно записать следующее:

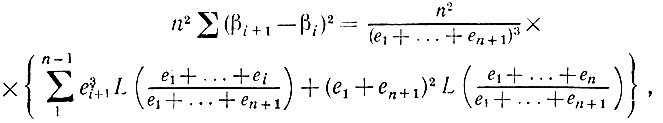(5.2.69)

где L(X) - индикаторная функция для интервала (β', β"). Если N достаточно велико, то выражение (5.2.69) с вероятностью, близкой единице, мажорируется сверху следующим выражением:

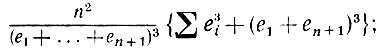(5.2.70)

здесь суммирование проводится в диапазоне от i = [(β' - ε)/n] до i = [(β" + ε)/n]; снизу же оно ограничено выражением

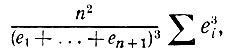(5.2.71)

здесь суммирование проводится в диапазоне от i = [(β' - ε)/n] до i = [(β" + ε)/n]. Но

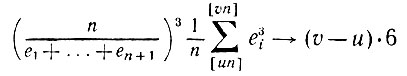(5.2.72)

по вероятности, так как E(e³_i) = 6. Кроме того, (e₁ + e_n+1)³/n → 0 по вероятности, так что при β_i∈(β', β")

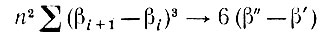(5.2.73)

по вероятности, откуда следует, что

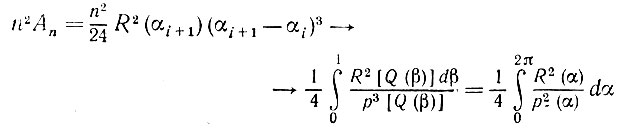
по вероятности.

Третья, последняя часть доказательства должна показать, что величина n²B_n стремится к нулю по вероятности (см. уравнение (5.2.41)). Введем множество

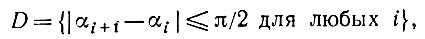(5.2.75)

так что искомую вероятность можно представить как

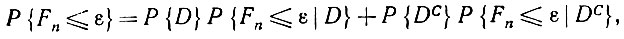(5.2.76)

где

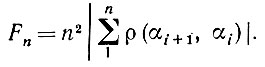(5.2.77)

Чтобы определить границы для входящих в (5.2.76) членов, прибегнем снова временно к равномерному распределению, обозначив R (0, 1) через Z с помощью порядковых статистик Z₁< Z₂ <... < Z_n, отождествляющих Z_{n + 1} с Z₁ по модулю единица, и введем событие А, связанное с (5.2.75):

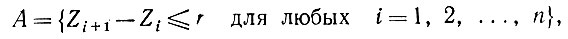(5.2.78)

где r - положительная постоянная, и событие B:

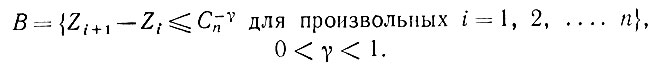(5.2.79)

Известно (см., например, Уилкс (1962), с. 334), что все случайные величины Z_i+1 - Z_i имеют плотность распределения вероятностей n(1 - x)^n-1, так что при C₁∈(0, 1)

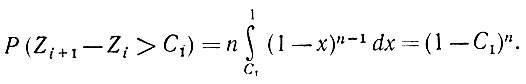(5.2.80)

Это приводит к следующему неравенству:

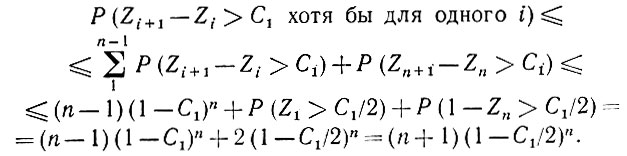(5.2.81)

Здесь мы воспользовались тем обстоятельством, что Z₁ и 1 - Z_n обладают, как указывалось выше, одной и той же плотностью распределения вероятностей.

Используя (5.2.81), получаем, что

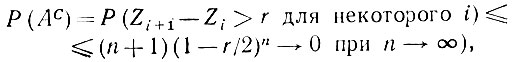(5.2.82)

если r < 1, и Р(А^с) = 0, если r ≥ 1. Для больших n имеем

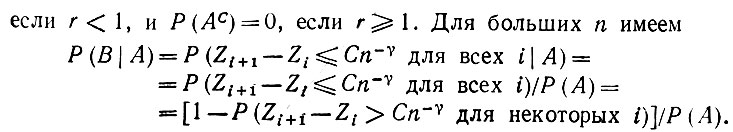(5.2.83)

Из неравенства (5.2.81), однако, следует, что

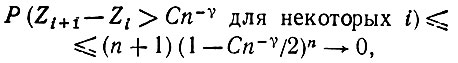(5.2.84)

и так как P(A) → 0, то очевидно, что P(В|А) → 1.

Вернемся теперь к случаю, когда мы имели плотность распределения р, и, как и выше, воспользуемся соотношением α = P^-1(Z). Тогда

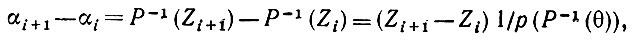(5.2.85)

где Z_i < θ < Z_i+1. Поскольку плотность p положительна и непрерывна, то очевидно, что при некотором δ > 0 справедливо

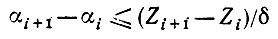(5.2.86)

и

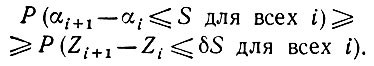(5.2.87)

Последнее неравенство с учетом полученных выше результатов приводит к тому, что

а для достаточно больших n

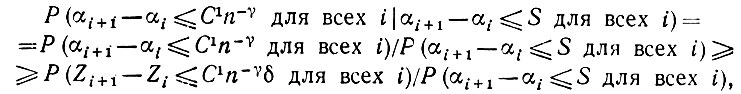(5.2.89)

что стремится к 1.

Выбирая

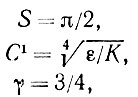
на основе (5.2.88) и (5.2.89) получаем, что

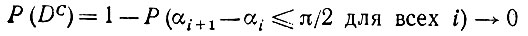(5.2.91)

и

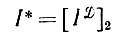(5.2.92)

Подстановка этих результатов в выражение (5.2.76) показывает, что F_n стремится по вероятности к нулю при n → +∞. На этом доказательство теоремы 5.2.2 заканчивается.

Замечание. Следует отметить, что в отличие от теоремы 5.2.1 данный результат связан не только со сходимостью математического ожидания нормированной ошибки восстановления: он показывает, что сама нормированная ошибка восстановления сходится по вероятности. По-видимому теорема 5.2.1 не поддается подобному обобщению.