5.3. Логика признаков второго порядка

Допустим теперь, что алгебра изображений строится на основе логики признаков второго порядка, а не первого, как в предыдущем разделе. Пусть образующие состоят из полуплоскостей, границы которых параллельны осям x и y, так что число классов образующих равно четырем. В этих условиях возникает алгебра изображений, рассмотренная в случае 3.5.13 т. 1.

К этому случаю нетрудно применить теорему 5.1.1, и в результате восстановление изображений по принципу максимального правдоподобия при действии деформирующих механизмов ₁ или ₂ определяется замыканием признаков I^D, т. е.

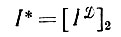(5.3.1)

(см. разд. 3.9, т. 1).

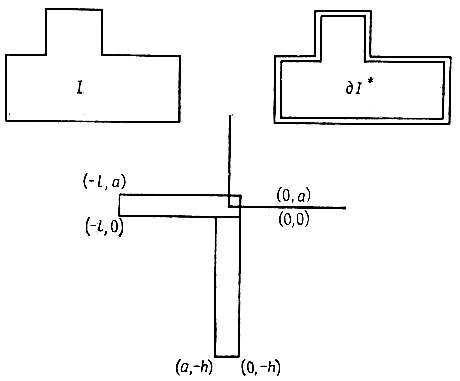
Разумеется, I^*⊂I, и поэтому ошибку восстановления можно записать как m(I - I^*), в результате чего мы непосредственно приходим к изучению характера зависимости подобной ошибки от идеального изображения и числа п точек, содержащихся в I.

Начнем с допущений, которым, как мы полагаем, должно удовлетворять идеальное изображение I:

(а) оно характеризуется конечной числовой сложностью и ограничено;

(б) при любом d > 0 связную непрерывную внутреннюю границу ∂I' можно провести так, что ее расстояние от ∂I равно самое большее d;

(в) оно не имеет "щупалец". (5.3.2)

Здесь условие (а) вводится лишь временно и позже будет ослаблено. Роль условия (б) заключается в том, чтобы исключить возможность возникновения на ∂∂I кратных точек (см. внутренний угол на рис. 3.5.17, т. 1) или нарушения ее связности. Условие (в) несущественно, поскольку щупальца имеют меру нуль и не порождают никаких составляющих деформированного изображения I^D.

При выполнении этих условий справедлива следующая теорема.

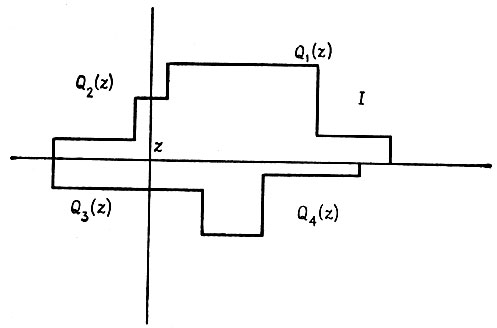
Рис. 5.3.1

Теорема 5.3.1. Если идеальное изображение подчиняется условиям (5.3.2), а деформированное изображение I^D возникает в результате воздействия механизма деформации ₁, то для ошибки восстановления справедливо

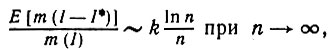(5.3.3)

где k - число внешних углов идеального изображения I.

Доказательство. Рассмотрим точку (x, y) = z∈I и введем четыре квадранта Q_i(z), t = 1, 2, 3, 4, сопоставленные z так, как

это показано на рис. 5.3.1. Если I^D = {z₁, z₂, ..., z_n}, то из определения замыкания по признакам следует, что

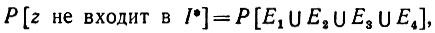(5.3.4)

где I^* = [I^D]₂ и E_i обозначает событие "ни одна точка z_i не входит в Q_i(z)". Правую часть выражения (5.3.4) можно переписать в следующем виде:

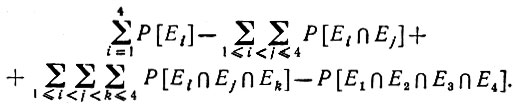(5.3.5)

Можно проанализировать асимптотическое поведение каждого из этих пятнадцати членов при увеличении n. Вычислить необходимо величину Е[m(I - I^*)]. Математическое ожидание площади разности можно записать как

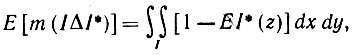
где I^*(z) и I(z) - индикаторные функции I^* и I соответственно. Но поскольку 1 - ЕI^*(z) есть вероятность того, что z не входит в I^*, то

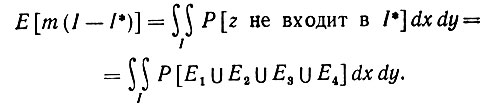(5.3.7)

Вычисление этих пятнадцати интегралов можно упростить, сгруппировав интегралы по типам и проанализировав каждый тип. Здесь присутствуют интегралы четырех типов:

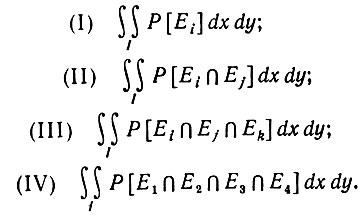
Тип I:

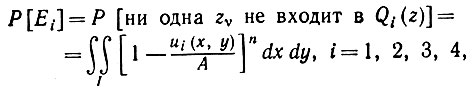(5.3.9)

где u_i(x, y) -площадь квадранта Q_i(z), содержащегося в I, и А = m (I).

Тип II:

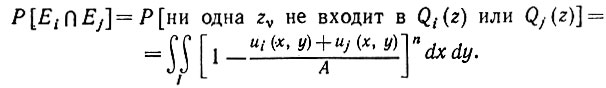(5.3.10)

Шесть интегралов этого типа определяются условием 1 ≤ i < j ≤ 4. Подобным же образом четыре интеграла определяются соответствующим условием для типа III.

Тип III:

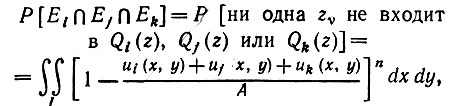(5.3.11)

Тип IV. Этот последний тип не вносит в (5.3.5) никакого вклада, поскольку мера E₁ ∩ E₂ ∩ E₃ ∩E₄ равна нулю.

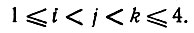
Рис. 5.3.2

Для того чтобы приступить к анализу асимптотического поведения этих интегралов, сформируем внутреннее множество I' с границей ∂I' (См. рис. 5.3.2), такое, что ширина тонких прямоугольных полос равна а. Тогда

Поскольку, однако, в I', u₁(x, y) > a², то

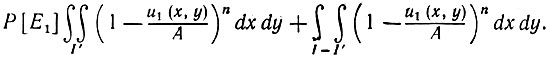(5.3.13)

Эта величина экспоненциально стремится к 0, и, как мы убедимся, ею можно пренебречь по сравнению с остальными вкладами.?

Теперь нужно вычислить вторые члены (5.3.12). Отметим, что условие u₁(x, y) < a² может выполняться только в пограничной области рис. 5.3.2. В остальных областях u₁(x, y) > a² и, как показано выше, вклад остальной части I - I' мал. Пограничную область можно разделить на небольшие прямоугольники ширины а, и интеграл по каждой из областей можно вычислить непосредственно:

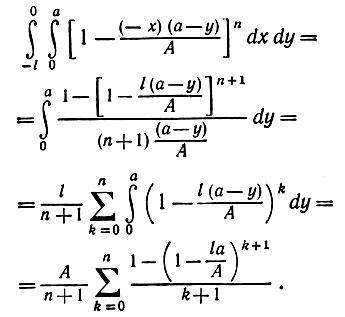(5.3.14)

Последнее асимптотически равно

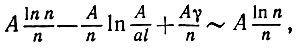(5.3.15)

где γ - постоянная Эйлера.

С другой стороны, для второго прямоугольника на рис. 5.3.2

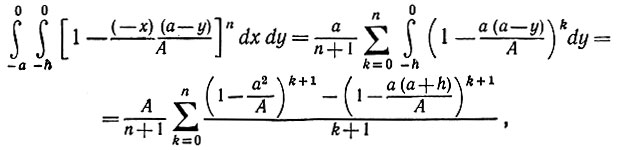(5.3.16)

что асимптотически равно

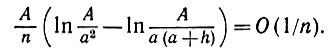(5.3.17)

Интегрирование по другим парам прямоугольных полосок проводится аналогично, и, таким образом, основной вклад каждой пары смежных полосок равен (А/n)ln n. Если внутри пограничной области (рис. 5.3.2) имеется kx внешних углов, то общий вклад в Еm(IΔI^*) будет равен (Ak₁ln n)/n.

Пограничная область на рис. 5.3.2 содержит множество точек, таких, что u₁(x, y) < a². Подобным же образом пограничную область, аналогичную представленной на рис. 5.3.2, можно построить так, чтобы u₂(x, y) < a². При этом, если новая пограничная область содержит k₂ внешних углов, то полный вклад в Еm(IΔI^*) будет равен (Ak₂ In n)/n. Поскольку каждый из этих внешних углов будет целиком содержаться только в одной из подобных пограничных областей, то полный вклад членов вида (5.3.9) можно записать как

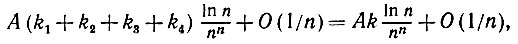(5.3.18)

где

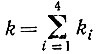
- общее число внешних углов I.

Остается показать, что члены вида (5.3.10) и (5.3.11) имеют порядок O(1/n) или меньший.

Для членов типа II

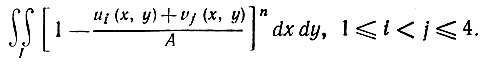(5.3.19)

Два случая (i = 1, j = 3) и (i = 2, j = 4) отличаются от остальных четырех случаев, в которых i и j задают смежные квадранты. Рассмотрим случай i = 1, j = 3. Точка z = (x, y) находится либо в I - I', либо в I'. Допустим, что z принадлежит I'. Тогда u₁(x, y) и u₃(x, y) превышают a² Следовательно, их вклад в (5.3.10) будет пренебрежимо мал при z∈I'. Допустим, что z принадлежит I - I'. В таком случае либо u₁(x, y) > a², либо u₃(x, y) > a². Итак, u₁(x, y) + u₃(x, y) > a², и этот вклад в (5.3.10) будет экспоненциально мал. Таким образом, в двух случаях (i = 1, j = 3) и (i = 2, j = 4) вклад будет малым.

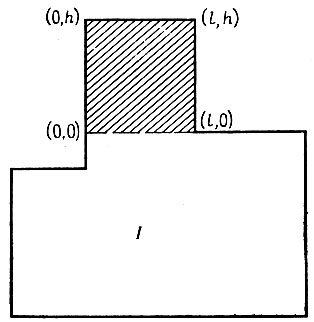
Рис. 5.3.3

Рассмотрим четыре оставшихся случая, в которых i и j определяют смежные квадранты. Следовательно, достаточно рассмотреть любой из этих четырех. Остановимся, скажем, на случае (i = 1, j = 2). Штриховка на рис. 5.3.3 отмечает прямоугольную область, которая может содержать все точки (x, y), такие, что u₁(x, y) +u₂(x, y) < a² при малых a. Очевидно, что не заштрихованная область содержит только те точки, для которых u₁(x, y) +u₂(x, y) > a², и, следовательно, соответствующий асимптотический вклад будет мал. Вклад, определяемый заштрихованной областью, равен

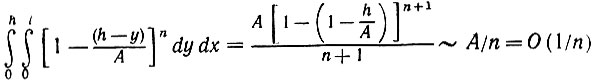(5.3.20)

Этот результат допускает непосредственное расширение на три остальных случая. Итак, общий вклад членов вида (5.3.10) равен О (1/я). Остальные четыре члена принадлежат типу (5.3.11), и если обратить внимание на то, что неотрицательная величина

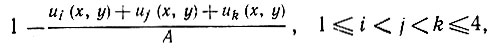(5.3.21)

самое большее равна

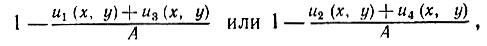(5.3.22)

то нетрудно убедиться, что они экспоненциально малы. Далее, интегрируя обе части соответствующего неравенства по I, можно убедиться в том, что члены типа III асимптотически пренебрежимо малы.

Подытоживая результаты анализа поведения типов I-III, приходим к выводу, что доказано следующее:

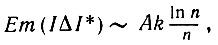(5.3.23)

где k - число внешних углов I. На этом доказательство теоремы 5.3.1 заканчивается.

Чтобы получить представление о скорости сходимости в этой предельной теореме, мы прибегли к машинному моделированию; часть результатов представлена на рис. 5.3.4 (без учета щупалец). Изображение I имеет k = 6 внешних углов; на картинках n = 20, 30, 50 и 100. Замыкания по признакам I^D представляют собой внутренние множества и, как можно убедиться, стремятся к I при увеличении n. Теоретические и эмпирические значения ошибок восстановления приведены в табл. 5.3.1. Рисунок показывает, что геометрическое восстановление не отличается высоким качеством, особенно во внешних углах.

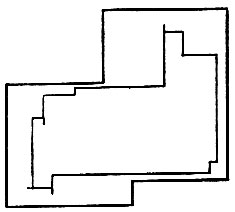
Рис. 5.3.4а

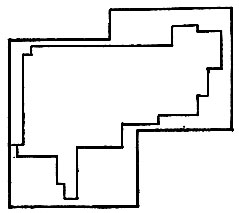
Рис. 5.3.4б

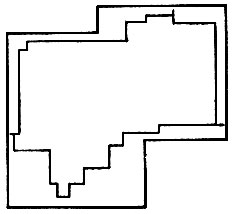
Рис. 5.3.4в

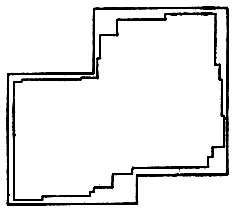
Рис. 5.3.4г

Таблица 5.3.1

Очевидно, что теоретическая оценка (5.3.3) завышает ошибку. Чтобы достичь более точной аппроксимации, мы снова возвращаемся к доказательству и, как и в (5.3.15), группируем члены порядка n^-1 и после ряда преобразований приходим ко второму приближению:

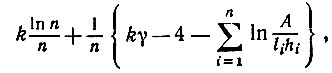(5.3.24)

где l_i - длина вертикальной стороны t-го внешнего угла, h_i - длина горизонтальной стороны i-го внешнего угла и γ - постоянная Эйлера. Очевидно, второе приближение точнее, однако следует иметь в виду, что в нем использовано не только качественное описание, отражающее число внешних углов, но также и результаты измерений длины сторон.

Отметим, что в последней теореме была доказана сходимость к конечному пределу математического ожидания нормированной ошибки восстановления. Неизвестно, сходится ли сама нормированная ошибка восстановления.

Если изображение характеризуется бесконечной числовой сложностью, имеет гладкую границу внутреннюю границу, аналогичную рассмотренной выше, то можно получить другой вариант предыдущего результата.

Теорема 5.3.2.Пусть I - изображение, замкнутое относительно логики признаков второго порядка, характеризующееся непрерывной положительной кривизной и удовлетворяющее указанному выше условию, наложенному на его границу. Построим I^D в соответствии с ₁ и его замыкание относительно логики признаков второго порядка I^* = [I^D]₂. Тогда асимптотически при n → +∞ справедливо

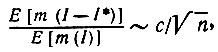(5.3.25)

где

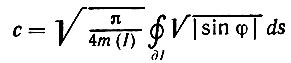(5.3.26)

и φ - угол, образуемый касательной к ∂I с осью x

Мы не будем приводить здесь доказательство, которое основано на вычислении интегралов типа I, II и III методом Лапласа. Заметим только, что второе приближение, улучшающее асимптотическое соотношение (5.3.25), получено не было, поскольку эмпирические результаты показывают, что уже первое приближение (5.3.25) достаточно точное.

На рис. 5.3.5 приведены два полученных на машине примера, в которых I - окружность, n = 30 и n = 100 соответственно.

Интеграл, входящий в (5.3.26), имеет интересную геометрическую интерпретацию. Подынтегральное выражение равно

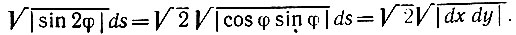
Интеграл

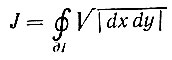(5.3.27)

в данном случае точно определен, и, согласно неравенству Шварца,

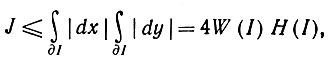(5.3.28)

где W (I) - ширина, а H(I) - высота идеального изображения. Равенство возникает, если |dy/dx| = const, что соответствует случаю, когда I - ромбовидное. Итак, при заданных размерах по осям x и y ромбовидная форма оказывается наиболее трудной для восстановления.

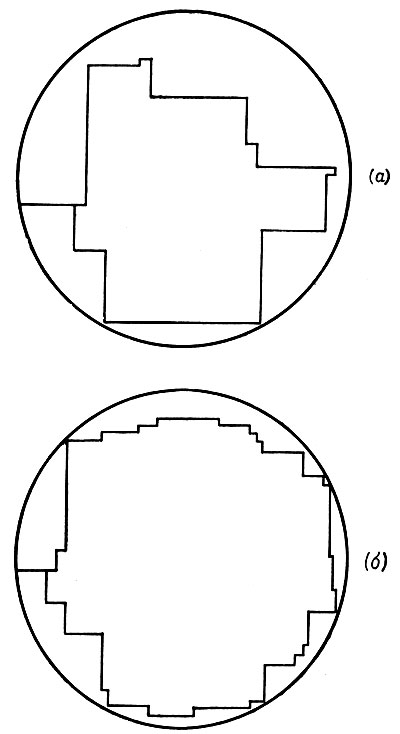
Рис. 5.3.5