5.5. Один результат, относящийся к аппроксимации изображения

В тех случаях, когда изображения представлены конфигурациями высокой или бесконечной мощности, приходится задумываться о более экономных способах хранения содержащейся в них информации. Разумеется, это приводит к некоторой потере информации, и возникает проблема нахождения оптимального способа.

Один из способов заключается в том, чтобы искать изображения, аппроксимирующие заданное и имеющие в то же время простые описания. В качестве примера рассмотрим случай, когда 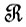"свободные" и в качестве R используется по меньшей мере столь же грубое правило, как "идентификация множеств образующих" (см. т. 1, с. 81). 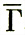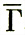Отметим, кстати, что может оказаться полезным ввести чуть более жесткое условие: два множества (конфигурации) образующих Γ₁ и Γ₂ отождествляются (по крайней мере), если совпадают их замыкания ₁ = ₂. Если множество G конечно, то, естественно, ни к каким топологическим понятиям прибегать не следует.

Как бы то ни было, воспользуемся правилом идентификации, согласно которому из c₁ = Γ₁ ⊂ G, c₂ = Γ₂ ⊂ G и Γ₁ = Γ₂ (как множества) следует c₁Rc₂; кроме того, это R отождествляет дополнения c'₁Rc'₂, где c'₁ = Γ^c₁ и c'₂ = Γ^c₂.

Пусть Γ_a - некоторое фиксированное инвариантное относительно S подмножество образующих; определим отображение f: 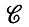→ 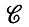как

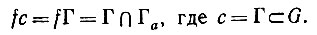(5.5.1)

Это непосредственно индуцирует отображение φ: 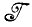→ 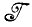как

В самом деле, (5.5.2) приводит к однозначному результату, поскольку, если с₁ = Γ₁ и с₂ = Γ₂ принадлежат одному и тому же изображению, то Γ₁RΓ₂ и, учитывая дополнения, Γ^c₁RΓ^c₂, кроме того, естественно, Γ^c_aR^c_a, так как R рефлексивно. Следовательно, исходя из пункта

(iii) определения 3.1.1 (т.1, гл. 3),

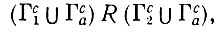<(5.5.3)br>

поскольку здесь соединение конфигураций означает просто объединение множеств образующих. Из (5.5.3) следует, однако, снова с учетом дополнений, что

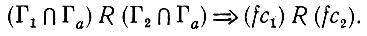(5.5.4)

Это доказывает, что отображение φ определяется однозначно.

Для доказательства свойства (ii) определения 3.1.2 (т. 1, гл. 3) обратим внимание на то, что

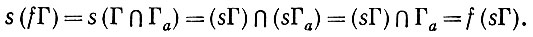(5.5.5)

Можно доказать также и свойство (iii) этого определения,

поскольку если Γ = Γ₁ ∪ Γ₂, то

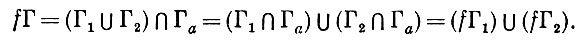(5.5.6)

Итак, мы доказали, что φ представляет собой гомоморфное отображение 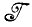в .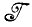

Если множество Γ_a достаточно плотно в G, то отображение φ можно рассматривать как некоторый оператор над изображениями, обеспечивающий аппроксимацию изображений более простыми изображениями. Рассмотрим один частный случай, связанный с предыдущим, но отличающийся от него: выпуклые множества изображений, которые нужно аппроксимировать выпуклыми многоугольниками, имеющими n сторон с направлениями 0, 2π/р, 4π/р, ..., 2(р-1)π/р. Такая аппроксимация не гомоморфна, так как [I₁ ∩ I₂]а не всегда равно [I₁]_а ∩ [I₂]_а. Можно лишь утверждать, что первое множество заключено во втором.

В таком случае можно исследовать асимптотическое поведение ошибки аппроксимации и получить удобное выражение, представляющее ее через кривизну изображения I. Однако вместо этого мы займемся более сложной задачей оптимального выбора n образующих из G с тем, чтобы сделать ошибку аппроксимации возможно минимальной.

Эта задача отличается от рассматривавшейся в разд. 5.4 тем, что в ней отсутствует случайный механизм деформаций ₄: вместо этого изображение I преднамеренно заменено некоторой его аппроксимацией I_a. Асимптотическая нижняя грань для ошибки аппроксимации была получена в работе Маклура и Вайтала (1975):

Теорема 5.5.1. Если изображение I представляет собой компактное выпуклое множество в пространстве R², имеющее гладкую границу с непрерывным радиусом кривизны r = r(θ), то

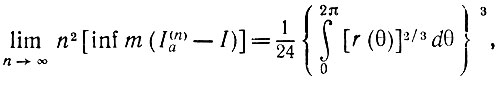(5.5.7)

где I⁽ⁿ⁾_a - описанный многоугольник с n сторонами.

Известен также конструктивный способ достижения асимптотической нижней грани. Введем функцию распределения

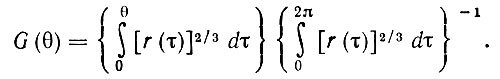(5.5.8)

Теорема 5.5.2.Пусть Iⁿ_a представляет собой последовательность наилучших описанных многоугольников с n сторонами, n = 1, 2, 3, .... Определим функцию распределения

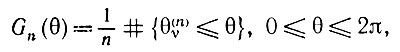(5.5.9)

где θ⁽ⁿ⁾_υ - направления нормалей к сторонам Iⁿ_a. Тогда

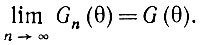(5.5.10)

Более того, если r строго положительна, и Iⁿ представляет собой последовательность описанных многоугольников с направлениями нормалей G^-1 (υ/n + 1), υ = l, 2, ..., n, то Iⁿ асимптотически оптимально.

Читатель, интересующийся доказательствами этих теорем, может найти их в уже упоминавшейся статье Маклура и Вайтала. В разд. 3.3 мы уже описали этот метод.

Очень мало в настоящее время известно об аналогичной задаче аппроксимации изображения в случае логики признаков более высокого порядка или других образующих.