5.7. Немного стереологии

Основная задача количественной стереологии - сделать выводы о распределении объектов в пространстве R³, исходя исключительно из неполных наблюдений одномерных и двумерных многообразий в этом пространстве. Другими словами, изображение I можно наблюдать только в тех точках, где оно пересекает некоторое окно w, и, следовательно, мы встречаемся здесь с деформацией маски (см. т. 1, определение 4.5.1, разд. 4.5).

Эта задача аналогична рассматривавшейся в предыдущем разделе, но отличается от нее тем, что здесь для изучения I используются не точки зондирования, а его сечения или проекции. Применению математических методов в стереологии в последнее десятилетие уделялось много внимания, и читателю, интересующемуся этой проблемой, мы рекомендуем обратиться к работам Дихоффа (1968) и Баха (1975), где он сможет найти ссылки на другие работы.

Параллельно в последние годы математики, работающие в теоретических областях, развили теорию случайных множеств. Эта теория явно стимулирована стереологической проблематикой, но имеет значительно более общий характер. В этой связи мы рекомендуем читателю работу Кендалла (1974) и монографию Матерона (1975).

Здесь мы сосредоточимся на кратком рассмотрении одной аналитической задачи из области стереологии, которая представляет существенный теоретический интерес и к тому же относится к важному классу трудных задач численного анализа.

Обратимся к задаче, рассмотренной на с. 330-331 т. 1. В пространстве R³ имеется пространственный образ с образующими в виде непересекающихся сфер, диаметры которых подчиняются неизвестной плотности распределения р(D); предполагаем лишь, что она достаточно гладкая и имеет значения р(x) = 0 при x > x_max. Преобразования подобия включают только евклидовы движения и равномерные изменения масштаба, а отношение связи не позволяет сферам пересекаться. Пространственный образ пересекается плоскостями, и получаемое в результате деформированное изображение состоит из окружностей, диаметры которых подчиняются некоторой плотности распределения q(D). Последние мы и наблюдаем, а найти хотим р.

В первом томе было показано, что

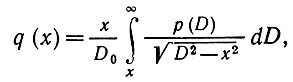(5.7.1)

где D₀ - математическое ожидание р. Решая интегральное уравнение Абеля первого рода, получаем, что

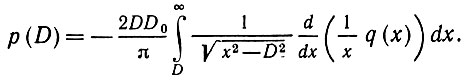(5.7.2)

Если сечение производится не плоскостями, а тонкими пластинами, например, при получении срезов с помощью микротома, уравнения следует несколько модифицировать (см. Бах (1975), с. 25).

Все это прекрасно и хорошо известно со времен основополагающей работы Уикселла, упомянутой в предыдущем томе. С точки зрения анализа образов, однако, решение выглядит не столь полным, поскольку вывод образа основывается на конечном числе наблюдаемых окружностей, скажем, с диаметрами D = x₁, D = x₂, ..., D = x_n, и мы не знаем q точно.

Мы будем рассматривать x₁, x₂, .. ., x_n как независимо тождественно распределенную выборку из плотности распределения q. Эта аппроксимация, естественно, неприемлема, если сферы размещены плотно. В последнем случае необходимо включить в рассмотрение ковариационные члены.

Используя значения D, можно построить оценку q^* плотности распределения, так что q^* → q в некоторой подходящей топологии при n → +∞. Отметим в то же время, что правая часть выражения (5.7.2) зависит от производной q и следовательно, как можно ожидать, будет чувствительна к меньшим вариациям при замене q на q*. Интегрирование (5.7.2) по частям тоже практически ничего не даст, и поэтому необходимо провести более тщательный анализ.

В литературе по стереологии можно найти алгоритмы для численного решения (5.7.1), см., например, Андервуд (1968). Хотя практически эти алгоритмы и могут быть полезными, они ничего не дают для теоретического осмысления задачи, которая имеет значительно более общее значение, чем можно предположить с первого взгляда.

Чтобы получить более определенное представление об основной трудности, обратимся к следующему интегральному уравнению первого рода:

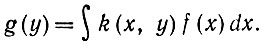(5.7.3)

В этом уравнении ядро k и функция g заданы; требуется найти I. Это классическая задача из области интегральных уравнений, и способ ее решения прекрасно известен, но если функция g задана не полностью, например подвергается воздействию шумовых возмущений, то теоретическое решение становится почти бессмысленным. Это объясняется тем обстоятельством, что I может не обладать непрерывной зависимостью от g. Таким образом, следует применять более изощренные методы решения; мы рекомендуем читателю обратиться к работе Турчина, Козлова и Малкевича (1970), содержащей обзор некоторых методов работы с подобными "некорректно поставленными задачами".

В нашем случае мы воспользуемся преимуществами, связанными со специальным видом уравнения. Это позволит нам разработать метод, который прекрасно подходит для решения нашей задачи. Сначала покажем, как можно получить состоятельную оценку функции распределения Р, но воспользуемся при этом способом, существенно отличающимся от обычных процедур оценивания и обладающим рядом озадачивающих свойств.

Теорема 5.7.1. Для произвольного фиксированного у сформируем величину

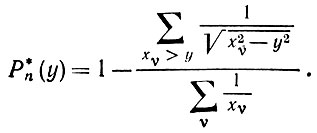(5.7.4)

Она является хорошо определенной почти наверное. Тогда P^*_n сходится почти наверное к P(y) при n → ∞.

Доказательство. Используя (5.7.2), изменив порядок интегрирования и интегрируя по частям, получим

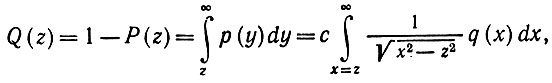(5.7.5)

где c = 2D₀/π - постоянная, нормирующая q, так что q(0) = 1. Рассмотрим при фиксированном y следующую случайную величину:

(5.7.6)

здесь x выбирается из распределения с плотностью вероятности q. В таком случае U имеет конечное математическое ожидание, равное

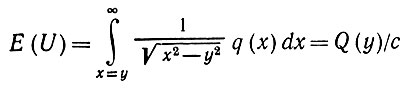(5.7.7)

и может быть получено с помощью (5.7.5). Следовательно, среднее значение, почти наверное:

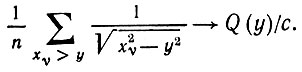(5.7.8)

С другой стороны, случайную величину 1/x, где x распределена в соответствии с q, можно определить с помощью (5.7.1), и, изменив порядок интегрирования, получаем

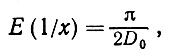(5.7.9)

так что

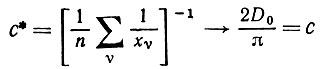(5.7.10)

почти наверное. Объединяя (5.7.8) и (5.7.9), приходим к пределу, указанному в формулировке теоремы; см. (5.7.5).

Замечание. Выражение (5.7.4) является состоятельной оценкой Р(y), но следует, однако, иметь в виду, что это не сама функция распределения. В действительности все ее x-точки особенные, и можно попытаться провести ее усечение, проводя суммирование только до x_υ > y + δ_n, где δ_n↓0 (медленно) при n → ∞. Очевидно, кроме того, что нельзя получить состоятельную оценку р(y) просто путем дифференцирования (5.7.4).

Мы можем получить ее с помощью регуляризации, а именно сглаживания. Чтобы несколько пояснить, начнем со сглаженной оценки q и воспользуемся ею для получения оценки р.

Рассмотрим следующую величину, которая будет использована для оценивания плотности распределения р:

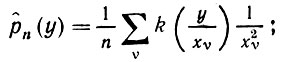
окно оценивания k остается пока произвольным с тем условием, что оно должно быть достаточно гладким. Математическое ожидание можно представить как

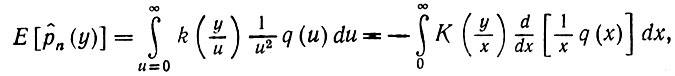(5.7.12)

где

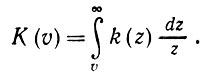(5.7.13)

Сопоставляя выражения (5.7.2) и (5.7.12), мы видим, что для уменьшения смещения окно k следует выбирать так, чтобы

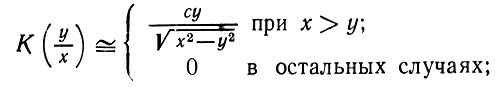(5.7.14)

это означает, что K(z) должно быть приближенно равно χ(z) = cz(1 - z²)^-1/2 при z < 1 и 0 в остальных случаях.

Мы уже показали, как можно оценить постоянную с отдельно (см. 5.7.10)). Введем одно параметрическое семейство C₁-функций K_α(z), обращающихся в нуль вне интервала (0, 1) и интегрируемых на интервале (0, 1) по мере dz/z². Тогда, положив r(x) = q(x)/x, можно ограничить смещение оценки 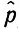_n с помощью

где R = sup |r(x)|, а использованная норма представляет собой L₁-норму при заданной мере. Следовательно, смещение можно сделать произвольно малым, выбирая Ка близким по этой норме к функции x и получая затем соответствующее окно k путем дифференцирования (5.7.13):

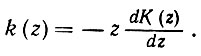(5.7.16)

Однако на этом пути мы встречаемся с затруднением. Действительно, вычислим дисперсию 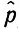_n (при условиях, оговоренных в начале этого раздела):

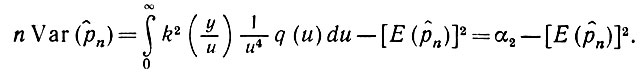(5.7.17)

Отсюда после некоторых вычислений получаем, что

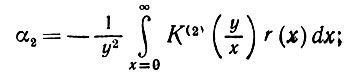(5.7.18)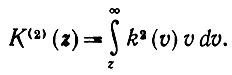

При приближении K_α к x окно k будет принимать очень большие значения - положительные и особенно отрицательные - вблизи z = 1. Это приведет к еще большим значениям квадрата функции, и можно считать, что K⁽²⁾(z) будет вести себя плохо. Поэтому α₂ будет стремительно увеличиваться, и следует позаботиться о том, чтобы K_α стремилась к x достаточно медленно, так чтобы коэффициент 1/n (см. левую часть (5.7.17)) был мажорирующим.

Все эти рассуждения можно суммировать в следующей теореме.

Теорема 5.7.2.Пусть проинтегрированное окно K_α принадлежит С₁(0, ∞), причем K_α(z) = 0 при z ≥ 1, а также

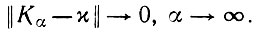(5.7.19)

Допустим, кроме того, что α = α_n стремится к бесконечности достаточно медленно, так, чтобы удовлетворялось условие

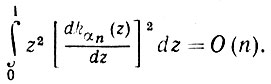(5.7.20)

Тогда оценка

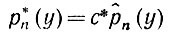(5.7.21)

состоятельна при n → ∞.

Замечание 1. Форма р^*_n (см. (5.7.21) и (5.7.11)) выбрана так, чтобы оценка была ковариантна относительно преобразований подобия. Действительно, если x_υ → ax_υ, где a - некоторый положительный масштабный коэффициент, то мы имеем

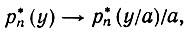(5.7.22)

что соответствует теоретическому соотношению р(y) → р(y/a)/a.

Замечание 2. По аналогии с замечанием, сделанным после теоремы 5.7.1, следует отметить, что p_n не является собственно плотностью распределения вероятностей: мы лишь утверждаем, что она сходится к плотности распределения вероятностей р при n → ∞.