Глава 6. Сетевые процессоры образов
6.1. Алгебра изображений микромира
Вообразим себе некоторое гипотетическое существо - назовем его Ω, живущее в некоторой среде или микромире, откуда оно получает сенсорные входные сигналы. Предполагается, что структура образов, с которой имеет дело Ω, в начале неизвестна и по мере течения времени й будет пытаться вывести ее. В данной главе мы будем рассматривать одну разновидность процессора образов, представляющего собой сеть, построенную из простых элементов. Наша цель -выяснить, как такой процессор может выводить образы и при каких условиях; кроме того, мы рассмотрим нормальные и патологические режимы работы сетевого процессора.
Прежде чем приступать к детальному изучению этих проблем, необходимо сформулировать общий подход, лежащий в основе нашего исследования, поскольку в принципе он отличается от подхода большинства исследователей, действующих в области математической психологии и математической нейрофизиологии. Напомним также, что мы обсуждали этот вопрос во введении.
Большая часть работ, выполняемых в этих областях, основывается на точке зрения, согласно которой роль математики в естественных науках заключается в квантификации и описании с максимально возможной точностью эмпирического знания, накопленного на данный момент. Основываясь на эмпирических данных, исследователь пытается сформулировать некоторую математическую модель изучаемого процесса, например запоминания, обучения, ассоциации или распознавания. Редукционист предпочел бы начать работу с уровня отдельной клетки, включить в модель сведения об электрохимических механизмах работы нейронов и использовать при этом всю ту детальную информацию, которую можно математически "переварить".
На этом уровне физиолог располагает неисчислимым количеством сведений, которое быстро увеличивается в связи с развитием в нейрофизиологии новых лабораторных методов исследования. К этому добавляются сведения, полученные физиологами- экспериментаторами на феноменологическом уровне. В течение нескольких последних десятилетий мы неоднократно были свидетелями попыток сформулировать математические модели, предназначенные для описания таких явлений, как обработка зрительной информации и обучение. Некоторые из этих попыток кажутся вполне удачными.
Изучение общих процессов мышления математическими средствами требует при таком подходе от нейрологии эмпирических данных по ряду специфических проблем. Исследование, в котором предлагается некоторая модель нейронной сети или какой-то ее части, должно основываться на сведениях о топологии этой сети. Естественно, эти сведения не должны быть исчерпывающими и не должны полностью определять матрицу инцидентности сети. Может оказаться вполне достаточно статистической топологии, но даже такой информации в настоящее время, по-видимому, не хватает.
Возьмем, например, другую проблему, неизбежно возникающую при исследовании обучения с помощью сетей,- синаптическую модификацию. Конечно, гипотеза о реализации долговременной памяти посредством изменений в синапсах восходит к началу столетия. В литературе многократно сообщалось о различных механизмах пластичности, подтверждающих эту гипотезу, но затем следовали лишь сомнения и вопрос о том, адекватна ли вообще эта гипотеза.
Некоторые физиологи, кажется, сомневаются даже в том, что на вопросы, задаваемые математиками по поводу сетей, можно будет дать определенные ответы в обозримом будущем, если только не будут совершены выдающиеся технические открытия. Верно это или нет -мы будем рассматривать эту проблему под совершенно иным углом.
Наш подход будет основан на дедукции, а не индукции по результатам наблюдений. При этом следует ввести ряд начальных допущений - мы прибегнем к аксиоматической постановке. Таким образом, наши допущения будут выставлены для всеобщего обозрения и станут доступны для критики и коррекции в случае необходимости. Мы сможем выяснить также, какие из допущений являются для полученных выводов ключевыми, а какие - второстепенными.
После того как постулаты выбраны, мы выводим из них следствия - геометрическим методом, как в любой дедуктивной системе*. Следовательно, истинность выводов определяется лишь анализом, проводимом в процессе доказательства, и истинностью аксиом. Это означает, естественно, что полученные выводы относятся исключительно к нашей гипотетической системе, но не к реальным нервным сетям.
* (Геометрическим в философской литературе XVII - XVIII вв. назывался метод, который аналогично методу, использованному Евклидом в геометрии, заключался в том, что вначале определялись исходные аксиомы, а затем из них с помощью логических правил доказательства выводилась истинность теоремы. В сущности геометрический метод-это предшественник аксиоматического метода современной науки. - Прим. перев. )
Выбирая аксиомы, мы без всякого сомнения будем вводить радикальные упрощения, которые могут противоречить, по крайней мере в определенной степени, тому, что известно относительно реальных нейронов и их связей. Наша цель заключается в том, чтобы построить логическую систему, по возможности простую и позволяющую прийти к результатам, которые отражали бы некоторые свойства обучаемости и памяти человека.
Вероятно, наиболее важные аксиомы - это те, которые характеризуют среду, порождающую сенсорные входные сигналы. Последние будут предполагаться существенно структурированными и, как ниже будет показано в рамках теории образов, обладающими регулярной структурой.
Кроме того, мы будем считать, что к моменту появления сенсорных входных сигналов в сети периферическая обработка уже выполнена. Это означает, что здесь мы не будем заниматься такими важными вопросами, как зрительное и слуховое восприятие. Основное внимание вместо этого будет сосредоточено на общих принципах вывода в некотором структурированном мире, точное наблюдение которого невозможно.
Допущение о высокой структурированности среды env (Ω), окружающей Ω, относится к числу основополагающих. Без допущения регулярности дальнейшие рассуждения будут лишены смысла. Если бы оказалось, что мир, в котором существует Ω, хаотичен и не обладает никакой или обладает очень небольшой регулярностью, то трудно понять, как могли бы быть организованы обучение и память. Действительно, нечему было бы учиться - в таком мире не было бы ни постоянных связей, ни законов.
Микромир env (Ω) будет состоять из материальных объектов, помещенных в трехмерное пространство. Для начала мы выберем ряд простых объектов, которые будут рассматриваться как твердые тела, обладающие определенными признаками. Они будут служить образующими в той алгебре изображений, которая будет построена нами.
Образующей g соответствует вектор признаков a(g), принимающий значения в некотором пространстве признаков. Функция признаков a(⋅) называется полной, если она разделяет образующие. Другими словами, если для двух образующих g и g' выполняется равенство a(g) = a(g'), то отсюда следует равенство g = g'. В нашем случае функция признаков будет полной, и поэтому мы можем, если захотим, идентифицировать образующие с помощью их векторов признаков. Это означает, что ω(g) так же, как показатели связи и индексы класса образующих, можно рассматривать как функции от вектора признаков. Разумеется, вектор а в целом необязательно должен быть доступен наблюдению Ω; подробнее этот вопрос рассмотрен в разд. 6.2.
Признаки формируются из частичных признаков различных типов. Для каждого типа υ значениями подвектора ах (g) будут булевы векторы конечной, но часто очень высокой размерности. Следовательно, любая компонента fυi(g) вектора aυ(g) может принимать лишь два значения: ИСТИНА и ЛОЖЬ; поэтому - бинарные признаки.
Тип признака может иметь различные физические интерпретации; приведем несколько примеров.
υ = 1: локализационный тип, характеризующий расположение отмеченной точки образующей g в пространстве R3.
υ = 2: ориентационный тип, характеризующий ориентацию g, например, с помощью двух углов или единичного вектора.
υ = 3: объемный тип, указывающий множество, покрываемое g со стандартными расположением и ориентацией.
На основе этих трех типов признаков можно вычислить другие производные признаки, например, такие, как V(g) - множество в пространстве R3, покрываемое образующей g при заданной ориентации, и т. п. Кроме того, можно определять объем m[F(g)], наибольший диаметр g и площадь ее поверхности. Две последние характеристики представляют собой примеры инвариантных частичных признаков.
Из конечно мерности и булевой природы вектора a(g) следует, что мы пользуемся некоторым конечным описанием микромира. Это не имеет значения для последующего -можно было бы пользоваться непрерывным описанием - это вопрос лишь математического удобства. Поскольку признаки будут иметь очень высокую размерность, различие кажется практически несущественным.
Если заданы две образующие g и g' и известны векторы aυ(g) и aυ(g') для υ = 1, 2, то можно определить совместные производные признаки, такие, как угол, образованный двумя отмеченными осями образующих g и g' соответственно. Если g и g' имеют анатомическую интерпретацию, например плечо и предплечье гибкой куклы из палочек, то можно определить угол соединения в локте. Аналогично обстоит дело в случае производных признаков, включающих более чем две образующие.
υ = 4: зрительный тип. Свет, порождаемый образующей g, будет характеризоваться по крайней мере двумя величинами - длиной волны и интенсивностью. Этого достаточно, если все точки любой образующей g излучают одну и ту же разновидность света. В противном случае потребуется большее пространство признаков, которое будет представлять информацию о неравномерном распределении света по g.
υ = 5: звуковой тип. Этот тип признака очень похож на тип v = 4; он описывает высоту тона, силу и другие характеристики звука, издаваемого g.
υ = 6: текстурный тип. Эти частичные признаки описывают автокорреляционные свойства распределения представленных в мелком масштабе высот поверхности, ограничивающей множество F(g'), или, что эквивалентно, спектральную функцию распределения.
υ = 7: температурный тип. С помощью этого типа частичных признаков характеризуется тепло, излучаемое образующей g или проводимое от нее.
Можно было бы ввести ряд других типов признаков: например признак, выражающий боль или удовольствие, испытываемое Ω при вступлении в контакт с некоторой образующей; запах и вкус - примеры еще двух признаков.
Вышеизложенное можно сформулировать в виде первой аксиомы для среды.
Аксиома Е1.Полное пространство признаков среды, в которой действует существо Ω, представляет собой прямое произведение
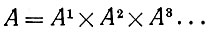 (6.1.1)
(6.1.1)
пространств признаков Aυ, каждое из которых состоит из конечномерных булевых векторов (fυi, i = 1,2, ...).
Для представления инвариантностей и постоянных взаимосвязей, существующих в мире, в котором живет Ω, введем отображения G → G - преобразования подобия. Они отражают то обстоятельство, что и объекты, и их комбинации существуют независимо от систем координат, используемых в пространствах признаков. В данном случае координаты представляют собой не просто некоторые координаты в опорном пространстве X = R3, т. е. физическом пространстве, но также и системы отсчета, используемые для представления света, температуры и т. п.
Чтобы придать нашим рассуждениям конкретный характер, будем считать преобразования подобия S группой переносов в R3 или соответствующей подгруппой, но следует заметить, что можно вводить и преобразования других видов, например повороты (или некоторую их подгруппу) или равномерные изменения масштаба (или некоторую их подгруппу). Если к тому же время присутствует в структуре образа в явном виде, то преобразования подобия могут включать также время, например преобразования Галилея. Пока мы будем требовать, чтобы преобразования подобия S удовлетворяли следующей аксиоме.
Аксиома Е2. Группа преобразований подобия S является конечной и абелевой, сохраняет инвариантность индекса класса образующих α(g):
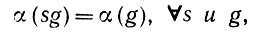 (6.1.2)
(6.1.2)
и отображает каждое Aυ в Aυ.
Замечание. Здесь, так же как и ниже, мы попытаемся выяснить, какая часть аксиоматики существенна, а какая менее важна. Условие (6.1.2) в аксиоме Е2 является стандартным для алгебр изображений. Остальные условия, однако, не представляются столь существенными и введены исключительно из соображений математического удобства. Немного неудобно иметь конечные S, т. е. просто группу подстановок, но это условие можно бы было, вероятно, исключить без серьезных последствий. Допущение о том, что 5 должно быть абелевой группой, трудно обосновать, и его следует ослабить.
Арность каждой отдельной образующей не будет ограничиваться (см. разд. 1.1, т. 1), причем связи подразделяются на исключающие связи и естественные связи. Каждая образующая будет иметь неограниченное число исключающих связей, показатели которых β(g) = V(g)- Соответствующее отношение связи ре является "ДИЗЪЮНКТНЫМ", так что
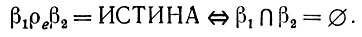 (6.1.3)
(6.1.3)
Образующая будет иметь также ряд (возможно, нуль, но всегда конечное число) естественных связей с номерами 1,2, ... . Соответствующие показатели связи заданы трехмерными векторами
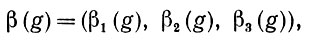 (6.1.4)
(6.1.4)
где β1(g) - некоторая отмеченная точка. Интерпретация такого показателя связи заключается в том, что он указывает возможное расположение соединения образующих. Отношение связи представляет собой "РАВЕНСТВО".
Показатель связи β2(g) -это пространственный угол, как указывалось выше, а отношение связи ρ2 означает "НЕДИЗЪЮНКТНЫЙ". Интерпретация состоит в том, что соединения не могут осуществляться под произвольными углами.
И наконец, β3(g) = α(g), т. е. просто индекс класса образующих. Это понадобится для того, чтобы допускать связи только естественно возникающих конфигураций.
В схемах конфигураций исключающие связи будут опущены, но следует иметь в виду, что они всегда будут возникать (см. далее). Эти связи не нужно снабжать числовыми метками, поскольку они идентичны для всех образующих.
Тип соединения 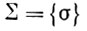 будет образован из
будет образован из
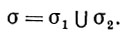 (6.1.5)
(6.1.5)
В данном случае σ∈ "ПОЛНЫЙ" относится к исключающим связям, а σ2 задается некоторым списком, использующим только информацию, содержащуюся в значениях индексов класса образующих, и характеризующим подтипы соединения для естественных связей.
Предложение 6.1.1. Множество 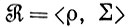 удовлетворяет условиям, определяющим регулярную структуру, и
удовлетворяет условиям, определяющим регулярную структуру, и 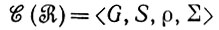 является пространством регулярных конфигураций.
является пространством регулярных конфигураций.
Доказательство. Необходимо показать, что отношения связи S-инвариантны (см. т. 1, с. 29). Во-первых, очевидно, что это действительно так для исключающих связей, поскольку, если g и g'- две образующие со соединением (βρeβ'-"ИСТИНА", принадлежащим σ1∈"ПОЛНЫЙ", то V(g) и V (g') не пересекаются. Отсюда следует, что перенесенные множества V(g) и V(g') также не пересекаются, и потому указанное отношение связи выполняется. Этот же прием применяется к отношениям 1 и ρ2 естественных связей: геометрический характер этих связей обеспечивает их инвариантность. Третье отношение естественной связи ρ3 не является геометрическим и, следовательно, к нему этот прием неприменим. Отметим, однако, что истинность ρ3 зависит исключительно от индексов класса образующих g и g', т. е. от α(g) и α(g'). Поскольку, однако, a(g) всегда S-инвариантен, то, следовательно, и ρ3 также инвариантно, на чем доказательство заканчивается.
Теперь мы готовы к тому, чтобы сформулировать третью аксиому для среды.
Аксиома Е3.Рассмотрим все конфигурации c = (g1, g2, ..., gn), регулярные относительно  , где n-любое натуральное число. Под потенциальной средой будем понимать среду, состоящую исключительно из этих конфигураций:
, где n-любое натуральное число. Под потенциальной средой будем понимать среду, состоящую исключительно из этих конфигураций:
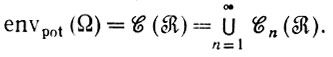 (6.1.6)
(6.1.6)
Среда для Ω не определяется целиком регулярностью  - эти правила лишь ограничивают возможные конфигурации множеством
- эти правила лишь ограничивают возможные конфигурации множеством 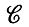 (
( ), но не говорят нам о том, какова вероятность встречи Ω с тем или другим расположением объектов, той или иной конфигурацией. Для уточнения этого момента требуется также некоторая мера Ω в пространстве конфигураций, позволяющая судить о том, что представляют собой вероятные конфигурации.
), но не говорят нам о том, какова вероятность встречи Ω с тем или другим расположением объектов, той или иной конфигурацией. Для уточнения этого момента требуется также некоторая мера Ω в пространстве конфигураций, позволяющая судить о том, что представляют собой вероятные конфигурации.
Аксиома Е4. Статистическая среда для Ω задается как
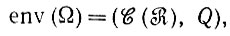 (6.1.7)
(6.1.7)
где Q - некоторая вероятностная мера, заданная на множестве 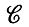 (
( ) допустимых конфигураций.
) допустимых конфигураций.
Вид распределения вероятностей, задаваемый вероятностной мерой Q на множестве 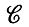 (
( ), определяет то, как Ω будет изучать свою среду. Так, Ω будет встречать только те конфигурации, которые принадлежат носителю Q, и поэтому естественно ввести опыт Ω(exp(Ω)):
), определяет то, как Ω будет изучать свою среду. Так, Ω будет встречать только те конфигурации, которые принадлежат носителю Q, и поэтому естественно ввести опыт Ω(exp(Ω)):
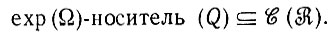 (6.1.8)
(6.1.8)
Мы, естественно, будем считать, что с течением времени регулярность  не изменяется. Это означает, что потенциальная среда
не изменяется. Это означает, что потенциальная среда 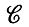 (
( ) не обнаруживает никаких тенденций, свойственных длительным периодам у временных рядов.
) не обнаруживает никаких тенденций, свойственных длительным периодам у временных рядов.
Если Q вообще не включает время, то мы будем говорить о стационарной статистической среде. Конфигурации в таком случае будут получаться независимо из exp(Ω). При этом имеет смысл рассматривать вероятность того, что Ω встретится с n объектами:
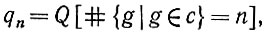 (6.1.9)
(6.1.9)
а также условное распределение на 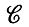 n(
n( ) для заданного числа образующих:
) для заданного числа образующих:
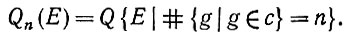 (6.1.10)
(6.1.10)
Если Ω встречается с различными конфигурациями, то Q определяет частоту появления возможных конфигураций. Последовательные конфигурации можно рассматривать как некоторый случайный процесс c(t), принимающий значения из 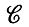 (
( ) и характеризующийся кусочно-постоянными реализациями. Значения c(t) тождественно независимо распределены в соответствии с Q при фиксированных значениях t, принадлежащих различным интервалам, на каждом из которых c(⋅) постоянен Q является их безусловным (одномерным) распределением. Вес, присвоенный некоторому определенному c∈
) и характеризующийся кусочно-постоянными реализациями. Значения c(t) тождественно независимо распределены в соответствии с Q при фиксированных значениях t, принадлежащих различным интервалам, на каждом из которых c(⋅) постоянен Q является их безусловным (одномерным) распределением. Вес, присвоенный некоторому определенному c∈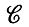 (
( ), будет тогда зависеть от того, сколь долго он может оставаться постоянным в процессе изучения.
), будет тогда зависеть от того, сколь долго он может оставаться постоянным в процессе изучения.
Если некоторая конфигурация c = (g1, g2, ..., gn) остается фиксированной в течение некоторого промежутка времени (t,t + Δt), то она представляет статическую среду, причем, если отрезок At мал, краткосрочную. Подобные конфигурации будут следовать одна за другой, почти как кадры в кино. Формализуем эту ситуацию.
Аксиома Е5. Функция конфигурации c(t) является кусочно-постоянной на временных интервалах переменной длины Δt. Значения c(t) определяются аксиомой Е4.
Выражаясь словами Лейбница, Ω видит свой мир как короткие проблески реальности. Мы еще не ввели никакой структуры для точечного процесса, образованного точками t, разделяющими статические среды.
Наблюдательные возможности Ω будут выражены через отношение идентификации R.
Аксиома Е6. Две регулярные конфигурации с и с', принадлежащие 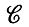 (
( ), идентифицируются по модулю R, если # (с) = # (с'), когда существует нумерация их соответствующих образующих такая, что gi = gi', i = 1,2,...,# (с), и когда их внешние связи одинаковы при использовании одинаковой нумерации.
), идентифицируются по модулю R, если # (с) = # (с'), когда существует нумерация их соответствующих образующих такая, что gi = gi', i = 1,2,...,# (с), и когда их внешние связи одинаковы при использовании одинаковой нумерации.
Тогда 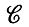 (
( )/R образует алгебру изображений (см. разд. 3.1, т. 1), и можно сформировать образы, которые Ω наблюдает в идеальных условиях.
)/R образует алгебру изображений (см. разд. 3.1, т. 1), и можно сформировать образы, которые Ω наблюдает в идеальных условиях.
В разд. 6.4 и 6.5, исследуя способности Ω к обучению, мы будем представлять возможно и невозможное в обучении на языке алгебры изображений  . Мы должны будем, однако, перейти к более конкретному языку, определяя, какого рода знания ?2 может приобретать, и нам придется построить соответствующую формализацию. Для этого мы воспользуемся языком исчисления предикатов первого порядка (см., например, Гильберт и Аккерман (1947) или Мейтс (1972).
. Мы должны будем, однако, перейти к более конкретному языку, определяя, какого рода знания ?2 может приобретать, и нам придется построить соответствующую формализацию. Для этого мы воспользуемся языком исчисления предикатов первого порядка (см., например, Гильберт и Аккерман (1947) или Мейтс (1972).
Высказывания относительно env (Ω) будут строиться на основе последовательного использования все более сложных комбинаций признаков. Простым высказыванием мы будем называть всякую дизъюнкцию простых признаков
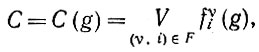 (6.1.11)
(6.1.11)где F - некоторое множество пар (υ, i). В качестве соответствующих примеров приведем следующие простые высказывания на естественном языке:
 (6.1.12)
(6.1.12)Среди этих высказываний все, за исключением третьего, являются однородными в том отношении, что в них используются признаки только одного типа.
Если С - простое высказывание, то его можно отождествить с его множеством истинности в G:
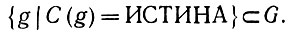 (6.1.13)
(6.1.13)
Дизъюнкция признаков соответствует, конечно, объединению множеств. Тогда определенные совокупности объектов можно описать с помощью относящихся к ним высказываний. Ясно также, что мы не можем описывать совокупности объектов, которые обладают признаками такого типа, как
 (6.1.14)
(6.1.14)Чтобы у нас появилась такая возможность, необходимо придать описаниям, высказываниям большую силу.
В качестве первого шага введем сложные высказывания второго порядка как
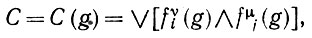 (6.1.15)
(6.1.15)
где дизъюнкция берется по некоторому множеству F четверок (υ, i, μ, j). Такое высказывание позволяет справиться с последними двумя совокупностями объектов в (6.1.12), но нес первой. В более общем виде, мы определим сложные высказывания порядка μ как
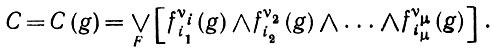 (6.1.16)
(6.1.16)
Другими словами, мы работаем с логикой признаков порядка μ, (см. Гренандер (1975), гл. 2) за исключением того, что поменялись местами роли дизъюнкций и конъюнкций. Как хорошо известно, между конъюнктивными и дизъюнктивными нормальными формами булевых выражений существует двойственность. Эти формы связаны друг с другом через отрицание. Поскольку обе формы математически эквивалентны, то выбор одной из них - просто вопрос удобства. В нашем случае, однако, это важный вопрос, так как мы хотим ограничить сложность формы либо в терминах дизъюнкций, как это сделано здесь, либо, наоборот, посредством ограничения конъюнкций. Тогда вопрос сводится к тому, что естественнее для описания env (Ω) - конъюнкция или дизъюнкция ограниченной сложности. Мы выбрали второй путь, но следовало бы остановиться на этом подробнее. Значение μ характеризует структурную сложность высказывания, а мощность множества F характеризует числовую сложность высказывания С.
Все это относится к случаю единственной образующей и также, естественно, к одноатомной конфигурации. Для произвольной регулярной конфигурации
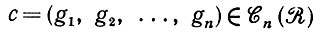 (6.1.17)
(6.1.17)
и соответствующего ей идеального изображения определим сложные высказывания порядка μ, в подпространстве конфигураций 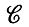 n(
n( ) как
) как
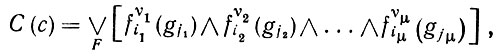 (6.1.18)
(6.1.18)
где F - некоторое множество значений (υ1, i1, j1, υ2, i2, j2,....,υμ, iμ, jμ). Здесь диапазон значений i определяется типами признаков; для заданного υ значение i самое большее равно размерности A, a j принимает значения между 1 и n = #(c).
При формировании высказываний типа (6.1.16) и (6.1.18) множество бинарных признаков F = {fυi} можно расширить за счет включения в него их отрицаний; в принципе это ничего бы не изменило, но дало бы некоторые удобства.
Высказывание самого общего вида записывается в соответствии с (6.1.16) или (6.1.18) в зависимости от того, имеем ли мы дело с единственной образующей или конфигурацией, причем число признаков в конъюнкции не ограничивается. Тогда мы получаем высказывания с неограниченной структурной сложностью.
То, что мы здесь делаем, сводится к следующему: рассматривая как исходные определенные предикаты - бинарные признаки, мы формируем более сложные предикаты. Это приводит непосредственно к исчислению предикатов первого порядка (при добавлении двух кванторов - квантора существования ∃ и квантора общности ∀). Рассматривая некоторое высказывание в техническом смысле этого слова в исчислении предикатов с переменными и индивидуальными логическими постоянными и сопоставляя его G или  (
( ), можно говорить об его истинности или ложности в среде, окружающей Ω. Обучение по своей природе имеет характер вывода, и было бы слишком потребовать, чтобы Ω мог быть абсолютно уверен в правильности своего ответа. Помимо всего прочего, контакт со средой env(Ω) не безграничен. Следовательно, имеет смысл ввести градации субъективной истинности или ложности вместо абсолютной истинности или абсолютной ложности; как это делается, мы увидим ниже.
), можно говорить об его истинности или ложности в среде, окружающей Ω. Обучение по своей природе имеет характер вывода, и было бы слишком потребовать, чтобы Ω мог быть абсолютно уверен в правильности своего ответа. Помимо всего прочего, контакт со средой env(Ω) не безграничен. Следовательно, имеет смысл ввести градации субъективной истинности или ложности вместо абсолютной истинности или абсолютной ложности; как это делается, мы увидим ниже.
Мы будем изучать обучение в следующем ограниченном смысле: установление количественных значений истинности высказываний относительно объектов и комбинаций объектов, находящихся в той среде, в которой существует Ω.
Полезно обратиться к нескольким конкретным примерам, а читатель может самостоятельно присовокупить к ним другие.
Пример 1. Запишем высказывание, устанавливающее, что две образующие g1 и g2 "совпадают по крайней мере по одному признаку υ-го типа". Пусть, например, они совпадают на каком-то участке цветового спектра. Это можно представить как
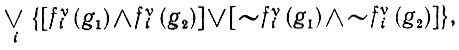 (6.1.19)
(6.1.19)
поскольку при любом i обе образующие либо удовлетворяют этому признаку, либо нет. Высказывание имеет порядок μ = 2, так как в него входят парные конъюнкции. Здесь мы включили в высказывание отрицания признаков.
Для упрощения записи логических формул типа (6.1.19) мы будем писать f' = f" для булевых выражений
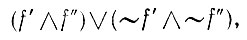 (6.1.20)
(6.1.20)
имея в виду, что символ " = " обозначает здесь отношение для парных признаков.
Пример 2. Допустим (но только в данном примере), что у объектов отсутствует протяженность, т. е. они являются точками, и их можно расположить на дискретной окружности единичного круга. Если υ "локализационный", принимаем i = 1, 2, ..., L; точки идентифицируются по модулю L. Циклическая группа, заданная на L объектах, является естественным выбором при определении преобразований подобия для признаков локализационного типа Slос. Высказывание "образующая g1 близка образующей g2" можно формализовать так: .
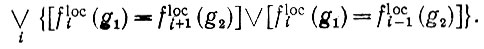 (6.1.21)
(6.1.21)Его порядок также μ = 2. Разумеется, вместо i + 1 и i - 1 можно было бы поставить другие отношения, так что "отношение ближайшего соседства", использованное в (6.1.21), заменяется обобщенным отношением "ближайшего в некотором смысле соседства".
Пример 3. Для некоторого высказывания С, заданного на G, факт наличия в потенциальной среде какого-либо объекта, для которого это высказывание справедливо, представляется следующим образом:
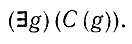 (6.1.22)
(6.1.22)
Подобным же образом, но заменив квантор ∃ квантором ∀, можно сформировать высказывание, утверждающее, что высказывание С справедливо для всех объектов в env(Ω).
Пример 4. Если на G заданы два высказывания C1 и С2 и если предполагается, что С1, имеет следствием С2, то можно построить высказывание
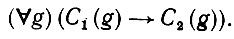 (6.1.23)
(6.1.23)
В этом высказывании, в частности, Ω может означать "лаять", а С2 -"иметь четыре ноги". Отношение импликации имеет μ = 1.
В особенности нас будут интересовать отношения, инвариантные относительно S. Так, во втором примере высказывание (6.1.21) не меняет своего истинностного значения относительно отображения 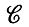 1(
1( ) →
) → 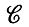 2(
2( ), определяемого переносами s∈S:
), определяемого переносами s∈S:
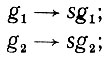 (6.1.23)
(6.1.23)здесь в обоих отношениях используется одно и то же s. С другой стороны, отношение "образующая g имеет локализацию i" не будет S-инвариантным.
Как же Ω при заданных структуре образов и языке высказываний относительно нее может сформировать представление о регулярности env (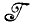 ) и как можно установить, что изображения, вероятно, удовлетворяют определенным высказываниям? Как Ω строит гипотезы о закономерностях у встречающихся ему образов, как Ω обобщает свой ограниченный опыт с тем, чтобы получить высказывания самого общего характера? Какие ощущения и ассоциации порождает у Ω встреча с идеальным изображением? В следующих двух разделах мы остановимся на всех этих проблемах.
) и как можно установить, что изображения, вероятно, удовлетворяют определенным высказываниям? Как Ω строит гипотезы о закономерностях у встречающихся ему образов, как Ω обобщает свой ограниченный опыт с тем, чтобы получить высказывания самого общего характера? Какие ощущения и ассоциации порождает у Ω встреча с идеальным изображением? В следующих двух разделах мы остановимся на всех этих проблемах.
По дидактическим соображениям мы будем использовать один пример, применяя его как стандартный случай в процессе продвижения вперед. Этот пример будет максимально возможно простым, однако его структура будет достаточной для выделения существенных допущений и особенно ограничений получаемых результатов.
Рассмотрим образующие с признаками двух типов: локализационными и цветовыми. Пусть локализационные признаки образующих представлены точками, расположенными на дискретной окружности, так что a1(g) принимает одно из значений x = 0, 1, 2, ..., L - 1, соответствующих углам 2π/L. Цветовой признак будет принимать значения а2(g) = 1, 2, 3, ..., nC, например 1-"ГОРИЗОНТАЛЬНАЯ", 2-"ВЕРТИКАЛЬНАЯ" и т. д. Если точка x не занята, мы будем представлять ее другим цветом пс+и например, условимся, что nC+1 - "БЕЛЫЙ". Цвет на рисунках мы будем представлять с помощью горизонтальной и вертикальной штриховки.
Группа преобразований подобия S будет представлять собой циклические перестановки L точек на дискретной окружности. Другими словами, подобие s можно идентифицировать прибавлением целого числа s к х по модулю L, s = 0, 1, 2, ....., L - 1.
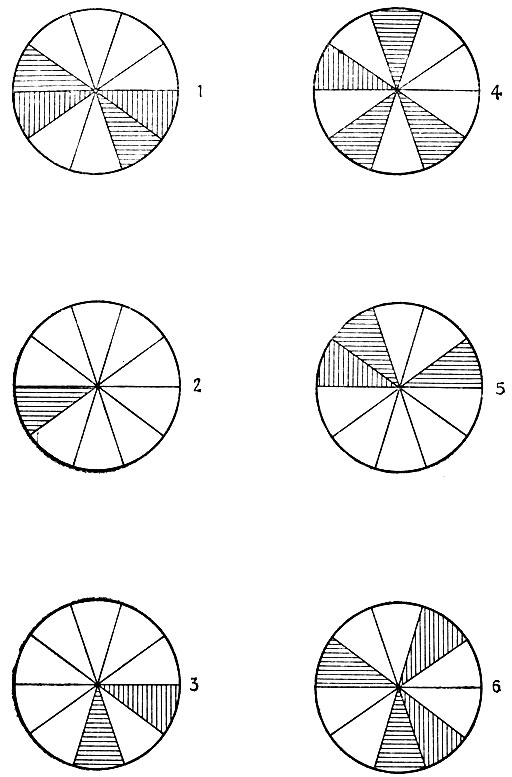
Рис. 6.1.1. а
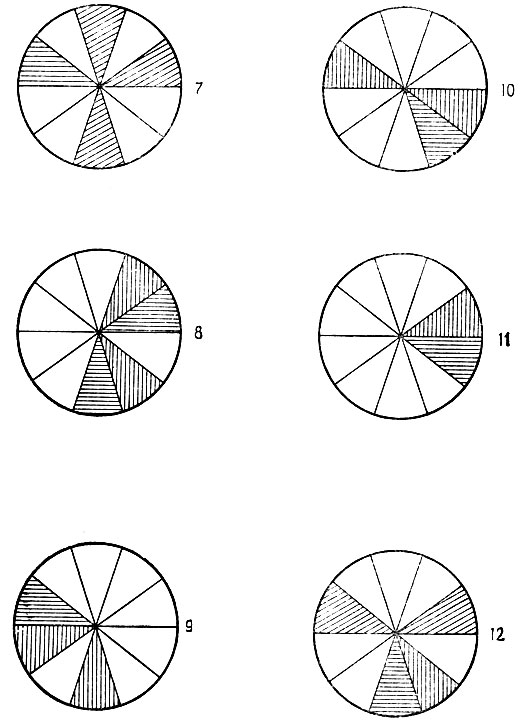
Рис. 6.1.1. б
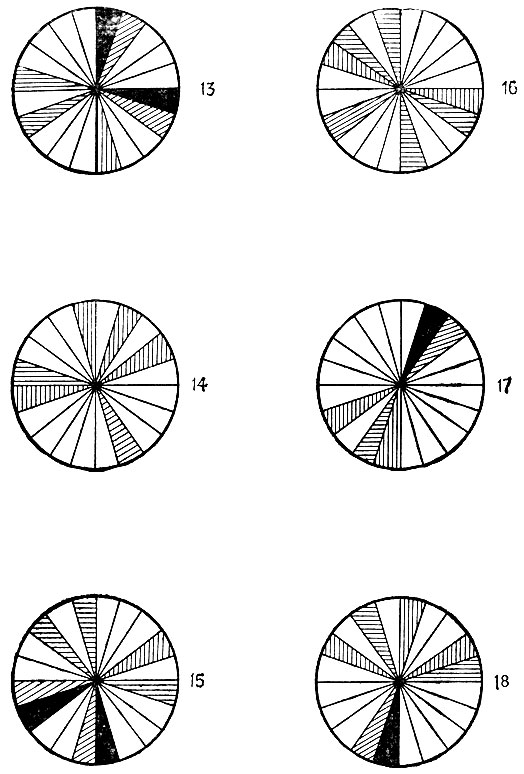
Рис. 6.1.1. в
Пусть α(g) - цвет (g), так что, поскольку индекс класса образующих должен быть S-инвариантным, цвет объекта не меняется при перемещении его из одного места в другое.
Поскольку мы имеем дело с одномерным случаем, то нет необходимости определять пространственные углы с помощью связи β2 - достаточно только β1 и β3. Последнее означает просто, что α - цвет. Для β1 выбираем одну из точек x ± 1/2:
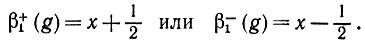 (6.1.25)
(6.1.25)Следовательно, наличие связи β1 между g и g' означает, что образующие g и g'- соседи и данное отношение симметрично относительно g и g'. В нашем примере мы примем ρ3 - "РАЗЛИЧНЫЕ", так что связанные смежные образующие в регулярных конфигурациях должны иметь разные цвета. В качестве типа соединения для σ2 (см. выше) выбираются все подграфы циклической цепи, причем σ2 - соединения x → x + 1 (см. (6.1.5)) - включают как крайний случай всю (циклическую) цепь 0, 1, 2, ..., L - 1.
Так определяется потенциальная среда Ω, и, кроме того, следует с помощью Q-меры задать статистическую среду. Это будет сделано в соответствии с общими положениями метрической теории образов (см. разд. 2.10, т. 1) и примечаниями к данному разделу.
На рис. 6.1.1а-6.1.1в приведены примеры, выбранные из трех простых статистических сред. На рис, 6.1.1а цветовой признак может принимать два значения: "ГОРИЗОНТАЛЬНАЯ" и "ВЕРТИКАЛЬНАЯ" (штриховка). Мера Q выбрана таким образом, чтобы связь "ГОРИЗОНТАЛЬНАЯ" → "ВЕРТИКАЛЬНАЯ" была сильной, а связь "ВЕРТИКАЛЬНАЯ" → "ГОРИЗОНТАЛЬНАЯ" - слабой. Значение "ГОРИЗОНТАЛЬНАЯ" появляется чаще, чем "ВЕРТИКАЛЬНАЯ".
На рис. 6.1.16 цветовой признак может принимать три значения: "ГОРИЗОНТАЛЬНАЯ", "ВЕРТИКАЛЬНАЯ", "КОСАЯ".
Третья статистическая среда, пример из которой приведен на рис. 6.1.1в, допускает четыре значения цветового признака: "ГОРИЗОНТАЛЬНАЯ", "ВЕРТИКАЛЬНАЯ", "КОСАЯ" и "ЗАЧЕРНЕНИЕ".
То, что мы здесь пользуемся признаками в виде штриховки, не должно приводить читателя к мысли о связи этого примера с иллюстрацией организации зрительного восприятия. Совсем наоборот, зрительная (и другая периферийная) предварительная обработка предполагается уже завершенной. Мы будем изучать организацию вывода образов, структурирующих мир.
Нас интересует, в частности, может ли Ω обучиться установлению истинности или ложности высказываний типа
"образующая g помечена КОСОЙ ШТРИХОВКОЙ";
"ВЕРТИКАЛЬНАЯ ШТРИХОВКА более вероятна, чем ГОРИЗОНТАЛЬНАЯ ШТРИХОВКА";
"образующая g расположена в х и не помечена ГОРИЗОНТАЛЬНОЙ ШТРИХОВКОЙ";
"конфигурация с содержит две смежные образующие";
"вероятно, что пара смежных образующих имеет тип ВЕРТИКАЛЬНАЯ ШТРИХОВКА-ГОРИЗОНТАЛЬНАЯ ШТРИХОВКА";
"существует конфигурация, содержащая некоторую пару"; "ГОРИЗОНТАЛЬНАЯ ШТРИХОВКА - ГОРИЗОНТАЛЬНАЯ ШТРИХОВКА".
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'