6.2. Наблюдаемые объекты

Если задана конфигурация образующих, в нашем случае объектов c = (g₁, g₂, ....,g_m), c∈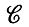(), регулярная в смысле , то как можно ее наблюдать, что представляет собой среда, передающая информацию о конфигурации нашему существу Ω? Как обрабатывается она на этапе предварительной обработки, прежде чем попадает в сеть 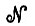, которая рассматривается в следующем разделе?

Мы начнем с одноатомной конфигурации, так что c = {g} состоит из единственной образующей g. Вектор ее признаков состоит из подвекторов a(g) (см. аксиому Е1). Вектор a(g) будет представлен в виде сенсорного вектора u(t), элементы которого принадлежат пространству U - сенсорному пространству, и мы будем считать, что признаки каждого типа обрабатываются независимо с помощью следующей процедуры.

В носителе информации применено импульсное кодирование с частотной модуляцией. Мы будем считать, что действительная частота повторения импульсов отличается от u_sp - самопроизвольной частоты повторения импульсов на положительную или отрицательную величину в зависимости от истинностных значений признаков в векторе признаков. Форма импульса будет фиксирована и точно задана на временной шкале ожидаемых между - импульсных интервалов.

Для признака каждого типа υ на A_υ будет задана некоторая алгебра множеств a^υ, индуцирующая на A алгебру-произведение:

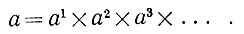<(6.2.1)br>

Алгебра множеств имеет следующую интерпретацию: она показывает, насколько подробна информация, содержащаяся в сенсорном входном сигнале. Если он очень информативен, т. е. Ω располагает мощной аппаратурой, то алгебра множеств является точной в техническом смысле слова, и наоборот.

Среди множеств, принадлежащих алгебре a^υ, выделим непустые множества, не содержащие собственных подмножеств; естественно, число подобных множеств конечно. Обозначим их через φ^υ₁, φ^υ₂,φ^υ₃,.....

Предложение 6.2.1.Множества φ^υ_j не пересекаются и перекрывают алгебру a^υ в том смысле, что всякое множество F∈a^υ можно представить как объединение множеств φ^υ_j.

Доказательство. Рассмотрим при любых i ≠ j множество

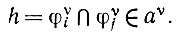(6.2.2)

Если h ≠ φ, то h = φ^υ_i или φ^υ_j, так как в противном случае оно было бы собственным подмножеством одного из них. Но оно не может быть равно, скажем, φ^υ_j, поскольку из этого следовало бы, что φ^υ_j⊃φ^υ_i, и, следовательно, возникает противоречие с определением множеств _j, указывающим на отсутствие пересечений множеств φ^υ_j.

Теперь мы покажем, что эти множества стягивают α^υ. Действительно, множество A^υ в целом представляет собой объединение всех множеств φ^υ_j, поскольку в противном случае

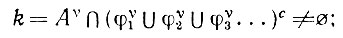(6.2.3)

a^υ - измеримое множество k не может, однако, не допускать разбиения на меньшие a^υ-измеримые множества, так как в этом случае оно оказалось бы равным некоторому множеству φ^υ_j, что противоречит (6.2.3). С другой стороны, его нельзя представить в виде объединения φ^υ_i1 ∪ φ^υ_i2 ∪, поскольку в этом случае

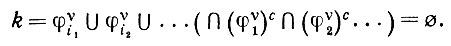(6.2.4)

Следовательно, k = φ, и поэтому

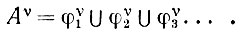(6.2.5)

Тогда для любого a^υ-измеримого множества F, принадлежащего получаем

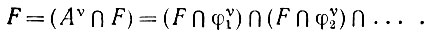(6.2.6)

В правой части выражения (6.2.6) имеет место либо φ^υ_i ⊆ F, либо φ^υ_i ∩ F = φ, поскольку множества φ^υ_i не поддаются разбиению. Это означает, что члены, входящие в объединение, либо равны некоторому множеству φ^υ_i, либо представляют собой пустые множества, на чем доказательство завершается.

Первая аксиома о наблюдаемых объектах будет сформулирована в виде условия измеримости относительно алгебр множеств

Аксиома 01. Сенсорное пространство U представляет собой прямое произведение признаковых сенсорных подпространств U¹, U²,... :

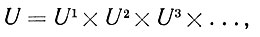(6.2.7)

и компоненты вектора и (g) в подпространстве U^υ определяются так:

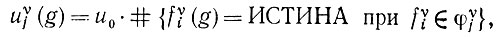(6.2.8)

где u₀ - случайная величина с нулевым математическим ожиданием и дисперсией V; для всех υ величина u₀ одна и та же. Носителем u₀ является вся ось действительных чисел, и в нуле дискретной вероятности не имеется.

Замечание 6.2.1. Роль случайной величины u₀ аналогична роли фазы в распространении волны: для всех классов признаков образующей g u₀ одна и та же, что можно рассматривать как условие когерентности.

Замечание 6.2.2. Такой способ кодирования не очень хорошо приспособлен для передачи информации об env (Ω), необходимой для того, чтобы Ω могло вывести структуру образа. Из дидактических соображений мы откладываем обсуждение соответствующей модификации до заключительной части данного раздела.

Замечание 6.2.3. Подобное кодирование ненадежно в том отношении, что множитель u₀ - величина случайная. Было бы целесообразно сделать его даже еще более ненадежным, добавив чисто случайный вектор к u(g) - аддитивный случайный шум. Влияние таких дополнительных деформаций вполне очевидно, и мы мало что потеряем, пренебрегая им в последующем рассмотрении

Замечание 6.2.4. Данный способ кодирования обеспечивает преобразование бинарных признаков с помощью алгебры множеств а в координаты вектора u. Это аналогично изучению некоторого заданного гильбертова пространства Н в случае, когда оно обязательно является пространством l₂, что не вносит никаких геометрических ограничений при сепарабельном Н, но может запутать общую картину. Кажется, однако, что можно осуществить кодирование бескоординатным способом так, чтобы бинарные признаки соответствовали подпространствам сенсорного пространства U, которые не должны быть просто координатными осями. Эту возможность следует изучить.

Все это относилось к отдельной образующей. Обратимся теперь к некоторой регулярной конфигурации c = (g₁,g₂, ...,g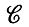_n)∈_n(). Кодировка u = u(g), описанная только что, дает нам некоторый сенсорный вектор и, воздействующий на сеть в течение определенного периода времени. Сначала g₁ представляется в виде u(g₁) и подается в течение некоторого времени на сеть 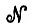, затем g₂ представляется в виде u(g₂) и подается на 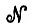и т. д. В дополнение к подобному кодированию мы будем допускать быстрое сканирование конфигурации, когда Ω пытается изучать конфигурацию как единое целое. Точнее, это означает, что конфигурация, у которой n > 1, предстает перед наблюдателем как нечто наподобие кадров фильма (мы уже говорили об этом в разд. 6.1). Вектор и как функция времени будет в таком случае некоторой периодической функцией, например с периодом Δt, так что

(6.2.9)

а затем следуют периодические повторения. Скорость сканирования по конфигурации с ограничена лишь инерционностью приборов, которыми располагает Ω: Δt₁ > t_scan. Максимальная длина кадра не ограничена. Во всех представлениях u(g₁), u(g₂),... будет использоваться одно значение u₀, т. е. для конфигурации в целом кодирование когерентно. Отношения (Δt_r)/Δt характеризуют внимание, уделяемое Ω образующим, из которых состоит наблюдаемая конфигурация объектов. Они представляют собой неотрицательные числа, прибавляемые к 1. Эти коэффициенты внимания характеризуют долю времени, уделяемую в процессе наблюдения каждому отдельному объекту. Мы оставляем открытым вопрос о зависимости этих коэффициентов от текущего состояния сети - пока достаточно указать, что они определены тем или иным способом. Все это можно формализовать так:

Аксиома 02.(i) Конфигурация, принадлежащая 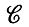(), представляется некоторой периодической кусочно-постоянной функцией времени, принимающей значения u(g₁), u(g₂), и т. д., причем кодирование когерентно.

(ii) Различные конфигурации представляются указанным способом, но с использованием статистически независимых значений u₀.

Другими словами, это означает, что, хотя для образующих, входящих в одну и ту же конфигурацию, кодирование когерентно, оно становится не когерентным для конфигураций, сменяющих друг друга по мере течения времени.

Вектор u, порождаемый конфигурацией с тремя образующими, может иметь вид, приведенный на рис. 6.2.1. Отметим, что время от времени некоторые подпространства "молчат". Сенсорное пространство U следует рассматривать как состоящее из множества подпространств, каждое из которых имеет высокую размерность, причем последняя для разных подпространств может быть совершенно различной. Использование алгебры множеств a^υ понижает размерность, однако ее влияние частично компенсируется вводимой ниже множественностью.

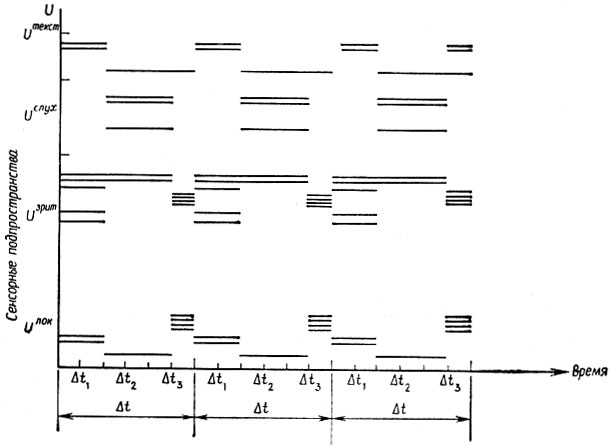
Рис. 6.2.1

Что же Ω реально может наблюдать и что не может? Следующая аксиома отвечает на этот вопрос. Обозначим через P_j^υ оператор проекции, который в U проектирует на j-е измерение ^υ_j υ-го сенсорного подпространства. Аналогично P^υ должен проецировать на υ-e сенсорное подпространство. Для определения энергии в пространстве U будем использовать L₂-норму:

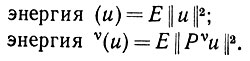(6.2.10)

В сенсорном подпространстве U^υ энергия ^υ(u) распределена между допустимыми компонентами, и это явление удобно характеризовать некоторой плотностью сенсорного энерговыделения Е (||P^υ_ju||²). Так, например, на рис. 6.2.1 третья образующая обладает высокой зрительной энергией в "верхней" части подпространства t/vis, первая и третья образующие характеризуются нулевой плотностью энерго-выделения в подпространстве U^and.

Аксиома 03. (i) Под наблюдаемым объектом мы понимаем линейный оператор L, получаемый как некоторая линейная функция проекционных операторов P^υ_j:

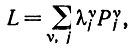(6.2.11)

где λ^υ_j - действительные постоянные.

(ii) Под наблюдаемым высказыванием мы понимаем наблюдаемый объект, представляющий собой некоторую проекцию.

Остановимся сейчас на значении вышеизложенного для способности Ω к обучению, но не будем, однако, пока определять его сетевой процессор 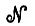. Мы рассмотрим, другими словами, чему оно могло бы обучиться в принципе, а не то, чему оно обучится на самом деле.

Итак, рассмотрим некоторую одноатомную конфигурацию c = {g}, переведенную в представление u(g) за время, в течение которого с наблюдалась. Повторим это наблюдение, воспроизведя конфигурацию несколько раз, т. е. воспользовавшись различными и независимыми значениями u₀ (см. аксиому 01). Для L, определяемого (6.2.11), Ω располагает, вообще говоря, значением ||Lu||² для повторяемых конфигураций. В таком случае закон больших чисел позволяет Ω вычислить математическое ожидание Е||Lu||² с любой точностью при увеличении числа повторений конфигурации с. Следовательно, математическое ожидание энергии всякого оператора L является величиной, доступной (теоретически) Ω.

В частном случае, когда оператор L обращается в некоторую проекцию Р^υ_j, эта величина принимает следующий вид:

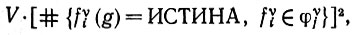(6.2.12)

так что известные значения математического ожидания энергии будут определять значения в квадратных скобках в (6.2.12), поскольку V - это известная постоянная. Следовательно, две образующие g и g' можно различить (теоретически) если

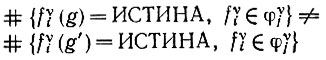(6.2.13)

по крайней мере для некоторых пар (υ, j)

Отображение

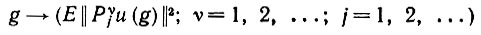<(6.2.14)br>

представляет G в виде векторов, компонентами которых являются целые неотрицательные кратные V значения. В экстремальном случае, когда а состоит из всех подмножеств A, значение этого отображения определяет значение истинности каждого бинарного признака f_i(g), так что g определяется однозначно. Если же а более ограничена, что соответствует менее мощному приборному оснащению Ω, то отдельные образующие не всегда можно отличить друг от друга даже теоретически.

Пусть S₀ - некоторая подгруппа S, сохраняющая инвариантность а, так что

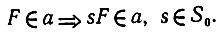(6.2.15)

Подобная редуцированная а-измеримая группа преобразований подобия будет тогда обладать тем свойством, что если g и g' неразличимы в принципе, то sg и sg' также неразличимы при любом s∈S₀. Действительно, 5 выполняет роль группы подстановок на множестве бинарных признаков f^υ_i (см. разд. 6.1) и применение s₀∈S₀ к φ^υ_j дает a^υ - измеримый результат, т. е. некоторое объединение

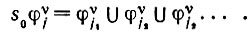(6.2.16)

Это означает, однако, что обратное преобразование s^-1 переводит, скажем, φ^υ_j1 в некоторое подмножество φ^υ_j. Это подмножество должно быть несобственным, поскольку преобразования s₀ сохраняют (считающую) меру и соотношение (6.2.16) выполняется. Итак, в правой части (6.2.16) содержится только один член; φ^υ_j переходит в некоторое φ^υ_j1. Однако тогда единственный эффект применения S₀ будет заключаться в том, что для g и g' будут одинаково переставлены значения истинности, что приводит к неразличимым конфигурациям.

Аналогичным образом приходим к следующему предложению.

Предложение 6.2.2.Отображения в U, индуцированные а-измеримыми преобразованиями подобия g → sg являются унитарными преобразованиями.?

Доказательство. Рассмотрим полную энергию u(sg). Ее можно представить как

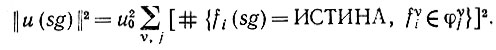(6.2.17)

Но преобразования подобия s просто переставляют бинарные признаки принадлежащие некоторому φ^υ_о, так что счетчики в правой части остаются теми же самыми, но перегруппированными. Следовательно,

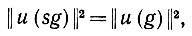(6.2.18)

из чего следует, что данное преобразование является унитарным.

Имеется также еще один результат этого же типа, и относится он к правилу идентификации R.

Предложение 6.2.3.Рассмотрим изображение, построенное из n образующих, и сформируем вектор (u(g₁), u(g₂), ..., u(g_n)) в пространстве U × U × ... × U (n раз). Отображение в этом пространстве, индуцируемое перенумерацией образующих, является унитарным оператором.

Доказательство. Оно проводится в основном точно так же. Достаточно лишь заметить, что здесь мы имеем перестановку координат в пространстве U × U × ... × U, и это автоматически определяет унитарный оператор.

Как же выглядят векторы u(g) для различных образующих? Ответить на этот вопрос можно, естественно, только в том случае, если нам известны env (Ω), а и распределение u₀. Следует, однако, иметь в виду, что используемые нами пространства имеют очень большую размерность, и, следовательно, "большинство" векторов почти ортогональны. Точнее, имеет место следующий экстремальный результат.

Предложение 6.2.4.При заданном распределении вероятностей Р в d-мерном пространстве U выберем р независимо тождественно распределенных векторов х¹, x², ..., х^p. Математическое ожидание квадрата объема р-мерного параллелепипеда (объем обозначим через Vol), одна из вершин которого расположена в начале координат, а ребрами служат векторы х, принимает минимальное значение

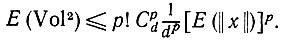(6.2.19)

Более того, при изотропном Р в (6.2.19) имеет место равенство.

Доказательство. Векторы x¹, x²,...,x^p будут стягивать p-мерное пространство или Vol = 0. В любом случае пусть u¹, u²,....,u^d-p - единичные векторы в R^d, ортогональные взаимно, а также всем векторам x. Тогда Vol = объему d-мерного параллелепипеда, образованного ребрами - векторами x¹,...,x^p и u¹,....,u^d-p. Объем можно, однако, записать в виде следующего определителя:

(6.2.20)

Строго говоря, здесь объем имеет знак. Возводя (6.2.20) в квадрат и выписывая соответствующие определители, получаем, что

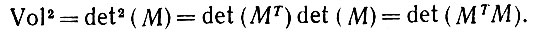<(6.2.21) br>

Но

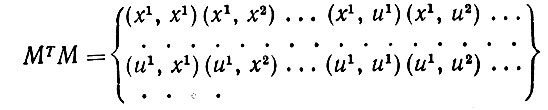(6.2.22)

или

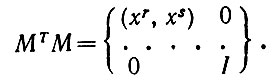(6.2.23)

Отсюда с учетом (6.2.21) следует, что

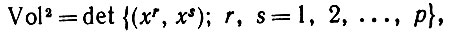(6.2.24)

и, выписав сумму произведений, получаем

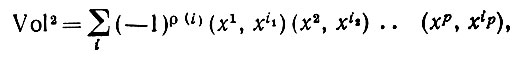(6.2.25)

где i = (i₁, i₂,...,i_p) - какая-то перестановка (1, 2, ..., р) и р(i) = ±1 в зависимости от того, четно или нечетно i.

Запишем выражение для математического ожидания величины (6.2.25) через моменты второго порядка (без вычитания средних значений), представленные в виде матрицы R:

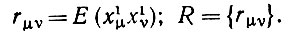(6.2.26)

Тогда

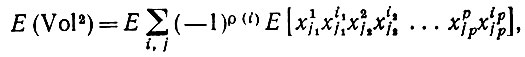(6.2.27)

где суммирование проводится по всем векторам перестановок i и по всем векторам j = (j₁, j₂,...,j_p), где j₁, j₂ ... принимают значения 1, 2, ..., р. Благодаря независимости векторов x^i₁ и x^i₂ при i₁ ≠ i₂ требуется найти лишь те k₁, k₂, ..., k_p, для которых выполняются условия

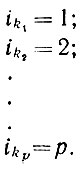(6.2.28)

Это вызвано тем, что в произведении, входящем в (6.2.27), можно брать x¹_jk1, x²_jk2 вместе с x²_jk2 и т. д. Следовательно, выражение (6.2.27) сводится к следующему:

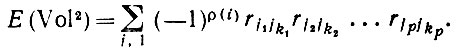(6.2.29)

Отметим, что k - это подстановка, обратная i (см. (6.2.28)), и поэтому оба значения либо четные, либо нечетные, ρ(i) = ρ(k) Но тогда

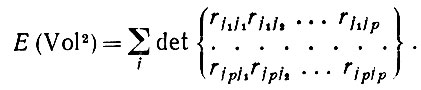(6.2.30)

При повороте системы координат объем не изменяется и можно, следовательно, предположить, что это уже было сделано для того, чтобы привести матрицу R к диагональной форме, скажем, R = diag [λ₁, λ₂,...,λ_d], Тогда

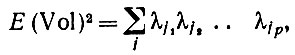(6.2.31)

где суммирование проводится по всем j, таким, что j₁, j₂, ... различные. Что касается остальных членов суммы (6.2.30), то у них по крайней мере два столбца идентичны и, следовательно, соответствующие определители равны нулю. Но выражение в (6.2.31) представляет собой однородный многочлен степени р от d неотрицательных собственных значений λ₁, λ₂,...,λ_d Другими словами, (6.2.31) пропорционально симметрическому среднему (см. Харди, Литлвуд и Пойа (1934)):

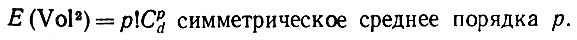(6.2.32)

Симметрическое среднее первого порядка - это просто среднее арифметическое:

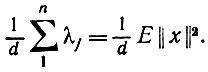(6.2.33)

Используя соотношение между этими двумя средними (см. Харди, Литлвуд и Пойа (1934)), получаем, что

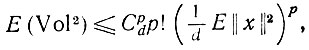(6.2.34)

т. е. выражение (6.2.19). В частном случае, когда распределение Р изотропно, все собственные значения равны 1/d Е||x||², так что (6.2.30) сводится к правой части неравенства (6.2.34); равенство достигается именно в этом случае.

Выберем теперь случайным образом в соответствии с P два вектора р = 2 и вычислим угол φ между ними:

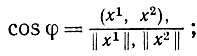(6.2.35)

этот угол точно определяется, если Р(x = 0) = 0. Спроектируем распределение Р на единичную сферу ||x||=1, проведя лучи через начало координат; полученное распределение обозначим через Р'. Очевидно, что cos φ имеет одно и то же распределение и при Р, и при Р'.

Тогда для Р' из теоремы следует, что математическое ожидание квадрата объема двумерного параллелограмма (квадрата площади) равно

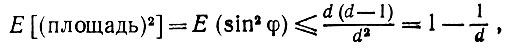(6.2.36)

и мы приходим к такому следствию.

Следствие 6.2.1. Для двух векторов, подчиняющихся распределению Р, имеет место следующее:

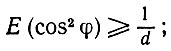(6.2.37)

равенство соответствует случаю изотропного Р.

Если, например, d = 10⁴ и Р изотропное, то можно считать, что угол примерно равен arccos 0.01 ≈ 89°,5. Векторы почти ортогональны.

Естественно, если р велико, то можно полагать, что каждый из С²_p углов будет вести себя так же, но совместное утверждение не выполняется. Если обратиться снова к распределению Р' и воспользоваться соотношением (6.2.34), то для изотропного распределения получаем

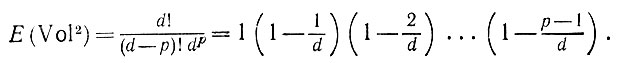(6.2.38)

Чтобы эта величина стремилась к 1, необходимо, чтобы р было по крайней мере меньшего порядка чем d. Сформулируем это точнее.

Следствие 6.2.2. Если распределение изотропно и

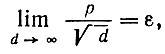(6.2.39)

то

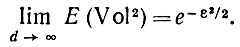
Доказательство. Из (6.2.38) следует, что

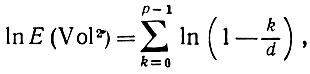(6.2.40)

так что при большой d и малом δ > 0 справедливо следующее:

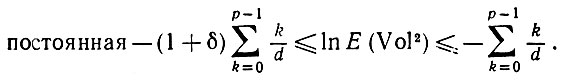(6.2.41)

Используя (6.2.39), можно ограничить значение Е (Vol²) сверху и снизу выражениями вида e^{-(ε2(1+O(1)))/2} откуда и следует искомый результат.

Это означает, что различные объекты, вероятно, имеют почти ортогональные векторы u(g). Следует, однако, соблюдать осторожность и не утверждать здесь слишком многого. Если два объекта g₁ и g₂ тесно связаны друг с другом, то наше предложение несправедливо. Так, в частности, маловероятно, что и (g) и u(sg) взаимно ортогональны. Скорее наоборот, можно считать,

что они близки друг другу в геометрии сенсорного пространства U.

Множество u(sg) при фиксированной g и произвольном s можно рассматривать как пучок векторов, образующих между собой небольшие углы. Два пучка, соответствующие не подобным образующим, стягивают два почти ортогональные подпространства. Это обстоятельство следует учитывать, приступая к обсуждению тех аспектов обучения, которые непосредственно зависят от геометрии сенсорных векторов.

В разд. 6.1 была введена статистическая среда, в которой действует Ω, и тем самым на сенсорном пространстве U было задано некоторое распределение вероятностей. Начнем с рассмотрения одноатомных конфигураций. Из (6.2.8) следует, что математическое ожидание сенсорного вектора равно нулю:

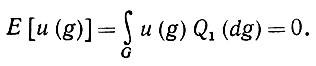(6.2.42)

Введем ковариации

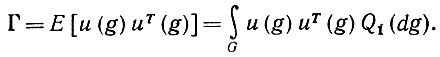(6.2.43)

В частном случае счетной среды, когда в ехр (Ω) могут входить лишь определенные объекты g₁, g₂, ..., характеризующиеся вероятностями Q₁(g₁), Q₂(g₂), ... , получаем, что

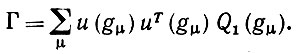(6.2.44)

Ковариации включают большую часть, но не все существенные факты об exp (Ω). Величину Γ мы будем называть оператором опыта-, этот оператор будет играть в процессе обучения фундаментальную роль.

Важное следствие предложения 6.2.4 заключается в том, что можно ожидать взаимной (почти) ортогональности u(g). Но тогда (6.2.44)-это (почти) спектральное представление оператора опыта. Таким образом, собственные векторы оператора опыта представляют собой (почти) сенсорные векторы существенно разных объектов, собственные значения которых (почти) равны

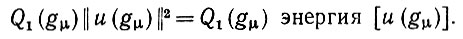(6.2.45)

Введем ядро в сенсорном пространстве U оператора опыта

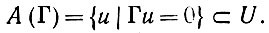(6.2.46)

Им будет удобно пользоваться при описании характеристик обучения. Мы будем придерживаться следующего представления А(Γ).

Предложение 6.2.5.Ядро A(Γ) для счетной среды с одноатомными конфигурациями представляет собой ортогональное дополнение линейного замыкания Lin {u(exp (Ω)}.

Доказательство. Произвольный сенсорный вектор и можно записать как

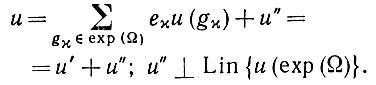(6.2.47)

Поскольку оператор Γ, определяемый выражением (6.2.44), обладает тем свойством, что Γu" = 0, то для того, чтобы обеспечить u ⊥ А(Γ), Γ" = 0, необходимо и достаточно выполнения условия Γu' = 0. Оператор Г, однако, является симметрическим, и его сужение на линейное замыкание Lin несингулярно. Действительно, если u - линейное замыкание u(exp (Ω)) и Γu = 0, то из (6.2.44)

следует, что

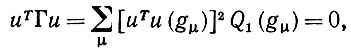(6.2.48)

и поэтому u ⊥ u (g_μ) для всех μ, поскольку Q₁(g_μ) > 0 для всех μ, так как мы ограничились носителем ехр(Ω) от Следовательно, u ∈ А(Γ) тогда и только тогда, когда u = 0, и поэтому и принадлежит ортогональному дополнению линейного замыкания. На этом доказательство заканчивается. В сущности предложение остается справедливым, если снять условие счетности.

Отображение и отображает exp (Ω) в, но не всегда на Lin. Отметим, что множество и (exp (Ω)) можно сделать линейно замкнутым, введя в exp (Ω) следующие фиктивные объекты. Если g₁ и g₂ ∈ exp(Ω), то, естественно, u = c₁u(g₁) + c₂u(g₂) ∈ Lin, но при этом не должно быть объекта g, такого, что u = u(g). Однако новый вектор и можно сделать соответствующим новому "объекту", учитывая, что всякое применение и включает реализацию u₀ (см. аксиому 01). Подбирая соответствующие значения u₀, можно добиться того, чтобы и был суммой, которая соответствует образующим, когда числа, входящие в правую часть (6.2.8),- это натуральные числа. Следовательно, признак определяется на а, и задан новый "объект".

Считается, что эти фиктивные объекты оказывают существенное влияние на характеристики обучения Ω. Отметим, что при построении фиктивных объектов используются различные значения u₀, т. е. действует условие не когерентности.

Если допустить в конфигурации более чем одну образующую, то в основном вышеизложенное сохраняет силу, за исключением небольших изменений. Когда Ω сканирует образующие g_υ, входящие в конфигурацию, каждая из них обрабатывается независимо от остальных, как указано выше.

Исключение составляет тот случай, когда скорости сканирования столь велики, а кадры Δt_i столь коротки, что необходимо учитывать инерцию . Как мы покажем ниже, это ведет к усреднению векторов u(g_υ), что имеет ряд важных последствий, которые будут обсуждены позже. Отметим сейчас лишь, что это делается в рамках когерентного кодирования и, следовательно, не соответствует прямо существованию фиктивных объектов.

Мы будем допускать, что на вектор у кроме механизма деформации g → u(g) налагается также аддитивный шум, так что в действительности наблюдается величина y + n, где n - некоторый не когерентный вектор белого шума, обладающий дисперсией σ²_n. Это не вызывает сколько-нибудь существенных изменений, т. е., влияние шума имеет меньшее значение, чем основная деформация и поэтому мы не вводим специальной аксиомы.

Преобразование кодирования u → u(g) до сих пор мы считали мгновенным, что вполне приемлемо, если образующие не изменяются быстро. Если же они изменяются быстро, то необходимо учитывать инерцию механизма деформации, что мы будем делать с помощью постоянной времени t_c.

Аксиома 04. Кодированное представление переменной входной величины определяется как

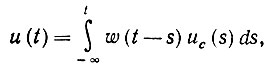(6.2.49)

где u_c(s) представляет величину, определяемую выражением (6.2.8) в любой момент времени s, u w-весовая функция.

Временное суммирование в (6.2.49), представляющее периферийную обработку, выражается, следовательно, с помощью временной весовой функции w, соответствующей постоянной времени t_c. Ее необходимо учитывать только в тех случаях, когда предъявляемые образующие быстро сменяют друг друга. Единственное допущение, необходимое для w(t), заключается в том, что w(t) = O(t^-2), t> 1 (см. предложение (6.2.10).

Как указывалось выше, кодирование, определяемое (6.2,8), не обладает мощностью, достаточной для передачи всей информации, необходимой Ω для изучения env (Ω). Нам требуется нечто большее, чем просто линейное кодирование, поскольку линейность предполагает наложение входных сигналов и исключает результаты взаимного влияния различных сенсорных координат. Откажемся на время от u₀ в (6.2.8), положив u₀ = 1. Мы решим данную проблему при помощи уплотнения (мультиплексирования) сенсорного вектора и введения входного поля у сети. Для этого нам потребуется следующая аксиома.

Аксиома 05.Для заданного сенсорного вектора u = u(g) сформируем уплотненный вариант (порядок уплотнения, или кратность m)

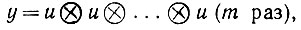(6.2.50)

где y принимает значения в пространстве входных сигналов

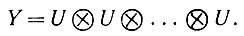(6.2.51)

Здесь необходимо снова ввести коэффициент когерентности u₀. Для этого по аналогии с (6.2.8) у в (6.2.50) заменяется на u₀. В данном случае u₀ обладает теми же, что и прежде, свойствами.

Оператор уплотнения ⊗ имеет следующий смысл. Если задан некоторый вектор υ = (υ_i), то его уплотненным с кратностью m вариантом является m-мерный массив с элементами υ_i1, υ_i2, ...,υ_im результат перемножения компонент. Кратность m отнюдь не столь велика, как исходные размерности U и U^υ.

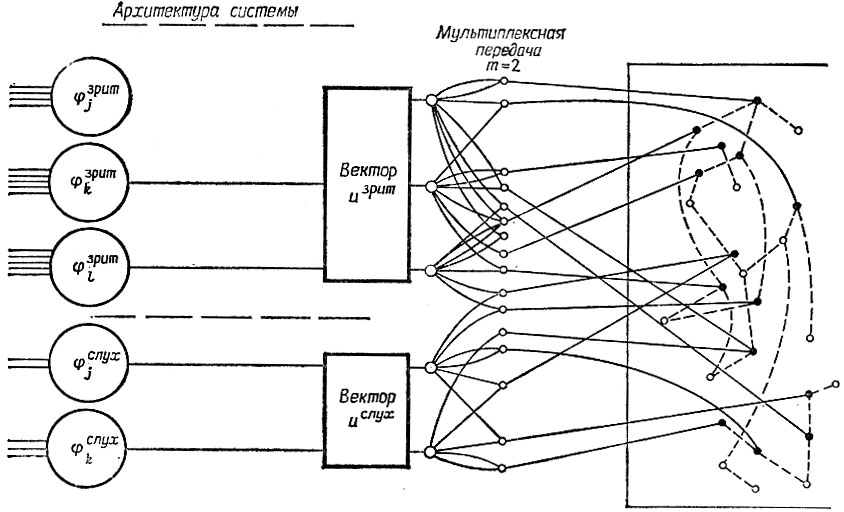
Рис. 6.2.2

Для простоты будет предполагаться, что во всей системе порядок уплотнения один и тот же. В качестве обобщения этого случая можно рассмотреть ситуацию, когда кратность изменяется в системе от 1 до некоторого максимума. Если, в частности, информационный носитель системы обладает высокой избыточностью, то целесообразно уплотнять лишь некоторую часть каждого сенсорного подпространства.

Рис. 6.2.2 дает представление о типе архитектуры системы, который мы имеем в виду. Источником линий, идущих слева, служат f^υ далее сигнал попадает в φ^υ_j, принадлежащие алгебре множеств a^υ, затем передается в виде сенсорных подвекторов u^vis, u^aud, u^lос и т. д. Они уплотняются с кратностью 2 и поступают в сеть (основной процессор) на входные ячейки, образующие подмножество _in. Входные ячейки представлены на рисунке зачерненными кружками, остальные - пустыми. Внутренние связи сети изображены пунктирными линиями. На этом рисунке показаны лишь отдельные уплотнения между U^vis и U^aud.

Ничто не мешает нам полагать, что уплотнение физически происходит в пределах основного процессора, если это представляется более естественным. Можно считать, что 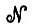- это основной процессор, включающий аппаратуру и программно-аппаратное обеспечение; система микропрограммирования последнего может модифицировать 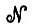, что будет рассмотрено ниже. Тогда можно говорить об уплотнении в результате вычислений в 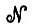, а не за счет каких-либо специализированных устройств.

Ниже мы убедимся в том, что полезно вводить частичное уплотнение порядка m. Последнее означает, что формируются не все возможные произведения компонент вектора u, а лишь часть из них.

Вернемся теперь к понятиям, рассматривавшимся в конце разд. 6.1, и сформулируем на их основе предложения, касающиеся операторов в пространстве входных сигналов Y. Начнем с одноатомных изображений. В соответствии с вышеизложенным Ω может самое большее идентифицировать объекты в той степени, в какой это допускает алгебра множеств a. Поэтому мы будем считать, что высказывания могут быть представлены в виде булевой функции от комбинированных признаков φ^υ_i.

Попробуем теперь сформулировать некоторое исчисление высказываний о наблюдаемых объектах, связывая соответствующие высказывания с операторами в пространстве входных сигналов Y.

Простое высказывание, содержащее признаки только типа υ, можно записать как

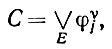(6.2.52)

где дизъюнкция берется по некоторому множеству Е пар (υ, j), Е ∈ a^υ

(1) Поставим в соответствие высказыванию (6.2.52) оператор в пространстве Y:

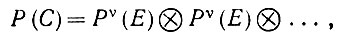(6.2.53)

где

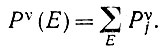(6.2.54)

Эта величина уже сама по себе является некоторой проекцией.

Напомним, что если Â = {a_ij} и В = {b_kl} - квадратные матрицы размерами d_A и d_B соответственно, то их прямое произведение Â ⊗ B "работает" в пространстве d_A ⊗ d_B, а его элементы имеют вид

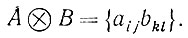(6.2.55)

(2) Если С₁ и С₂ - высказывания, операторы которых вычислены и являются коммутативными, то дизъюнкции этих высказываний следует поставить в соответствие оператор

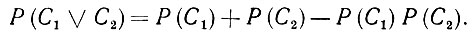(6.2.56)

(3) Если Р (C₁) и Р (С₂) вычислены и являются коммутативными, то можно определить

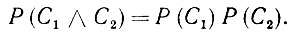(6.2.57)

(4) Если оператор Р, соответствующий некоторому высказыванию С, вычислен, то ~ С соответствует I - Р.

Теперь применим эти правила к высказываниям вида

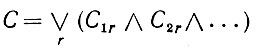(6.2.58)

(где все C_υr - простые высказывания для υ-го признака), используя сначала правила (6.2.53) и (6.2.57) для конъюнкций, а затем повторно правило (6.2.56) с тем, чтобы получить оператор, соответствующий (6.2.58).

Предложение 6.2.6. Оператор, соответствующий высказыванию, представляет собой некоторую проекцию.

Доказательство. Лучше всего начать с замечания о том, что все проекции P^υ_j коммутативны; в действительности они ортогональны. Формирование сумм Р^υ_j не нарушает коммутативности. В самом деле, все операторы, построенные с помощью описанной процедуры, коммутативны.

Оператор (6.2.53) должен быть проекцией, поскольку он симметрический, неотрицательный и идемпотентный. Последнее является следствием

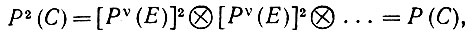(6.2.59)

если учесть, что [P^υ(E)]² = P^υ(E) и что для прямых произведений операторов имеем

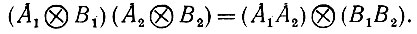(6.2.60)

Поскольку, однако, произведения коммутируемых проекций также являются проекциями, то и

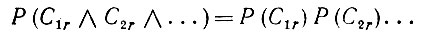(6.2.61)

есть проекция. Наконец, операция (6.2.56) снова приводит к коммутируемым проекторам, и, следовательно, доказательство завершено.

Важно осознать роль операторов проекций как активирующих факторов, представляющих высказывания. Введем в связи с этим следующее предложение.

Предложение 6.2.7.Оператор, построенный для высказывания, С, как описано выше, почти наверное активируется некоторым сенсорным вектором u = u(g) тогда и только тогда, когда C(g) = ИСТИНА.

Доказательство. Пусть С(g)= ИСТИНА. Тогда для (6.2.58) должно существовать r, такое, что

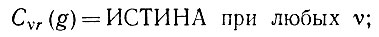(6.2.62)

следовательно, вектор и имеет ненулевую компоненту в подпространстве, соответствующем множествам Е^υ_r признаков φ, с вероятностью единица (см. последнюю фразу аксиомы 01). Но это означает, что у обладает ненулевой компонентой в подпространстве Y, проектирование в которое обеспечивает Р(C_1r∧C_2r∧....). Мы воспользовались здесь для y = u⊗u⊗....⊗y и простым, но очень важным соотношением

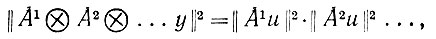(6.2.63)

представляющим свойство мультипликативности нормы в пространстве входных сигналов Y. Отметим, однако, что

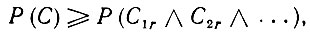(6.2.64)

причем неотрицательные операторы упорядочены. Следовательно сенсорный вектор и активирует Р(С), как и утверждалось.

Для завершения доказательства предложения 6.2.7 допустим, что Р (С) активируется некоторым сенсорным вектором u, так что

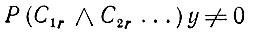(6.2.65)

для некоторого y. Действительно, если для двух коммутативных проекций Р₁ и Р₂ выполняется

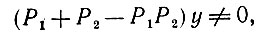(6.2.66)

ТО либо P₁y ≠ 0, либо Р₂y ≠ 0, и соответствующая итерация показывает, что (6.2.62) справедливо. Но тогда повторное обращение к мультипликативному соотношению (6.2.59) показывает, что Р(С_jr)u ≠ 0 при любых j, отсюда

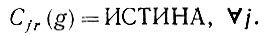(6.2.67)

Последнее означает, что С(g) = ИСТИНА, на чем доказательство и заканчивается.

До сих пор у нас нет гарантии в том, что данный способ преобразования высказываний в проекции гарантирует однозначный результат. Тем не менее это так.

Предложение 6.2.8.Если некоторое высказывание С может быть представлено двумя проекциями Р₁ и Р₂, то это означает, что P₁ = P₂

Доказательство. Отметим, что два множества Y, активирующие Р₁ и Р₂ соответственно, одинаковы независимо от вида заданного булева выражения С. Это непосредственное следствие предыдущего предложения. И Р₁ и Р₂, однако, являются проекциями. Проекции однозначно определяются множеством, в которое они проектируют. Поскольку они одинаковы для Р₁ и Р₂, то предложение справедливо.

С помощью этого исчисления высказываний о наблюдаемых объектах можно оперировать такими понятиями, как в (2.58). Ну а что же делать, когда появляются кванторы? Пусть C - высказывание, и нас интересуют высказывания типа

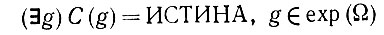(6.2.68)

или

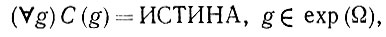(6.2.69)

или комбинации подобных общих высказываний об env (Ω).

Воспользовавшись Lin(Ω), равным линейному замыканию y(ехр(Ω)), y-отображению exp(Ω), можно получить ответ на этот вопрос в простой форме.

Предложение 6.2.9.(i) Высказывание (6.2.68) эквивалентно тому, что Р (С) не ликвидирует Lin (Ω). (6.2.70)

(ii) Высказывание (6.2.69) эквивалентно тому, что Р (С) не ликвидирует ни один элемент y-отображения exp (Ω). (6.2.71)

Доказательство (i). Если (6.2.68) справедливо, т. е. существует некоторая образующая g∈exp(Ω), удовлетворяющая С, то мы знаем, что y(g) почти наверное таково, что Р (С) y(g) ≠ 0 (см. предложение 6.2.7), и, следовательно, Р(С) не ликвидирует Lin(Ω). Если, с другой стороны, существует некоторый элемент fy∈Lin(Ω), причем Р (С) у Ф 0, то можно аппроксимировать у:

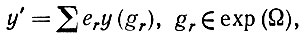(6.2.72)

причем Р(С)y' ≠ 0. Но это означает, что существует одна образующая g_r, такая, что Р(С)y(g_r) ≠ 0, или снова на основании предложения 6.2.7, что С (g_r) = ИСТИНА.

Доказательство (ii). Утверждать, что (6.2.69) справедливо - это то же самое, что утверждать Р(С)y(g) ≠ 0 для любой g∈exp (Ω), откуда доказательство следует непосредственно.

Следовательно, можно сказать, что логика переводится в операторные соотношения. Несколько простых примеров помогут читателю увидеть это более отчетливо.

Пусть высказывание С, влечет другое высказывание С₂, C₁ → С₂, ∀g∈exp(Ω). Что же привносит для соответствующих проекционных операторов Р₁ = Р(С₁) и Р₂ = Р(С₂)? Импликация справедлива только, если (~C₁)∧С₂ в exp (Ω) тождественно ложна, и, следовательно, соответствующая проекция, суженная на Lin(Ω), должна удовлетворять условию

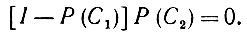(6.2.73)

Отсюда

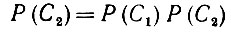(6.2.74)

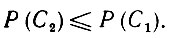(6.2.75)

И наоборот, если (6.2.74) выполняется, то импликация справедлива.

Аналогично, если два высказывания С₁ и С₂ являются в exp (Ω) взаимоисключающими, то Р(С₁) и Р(С₂) ортогональны.

Кроме того, если С₁ и С₂ взаимоисключающие и одно из них истинно, т. е. С₁ ∨ С₂ = ИСТИНА, то Р(С₁) + P(С₂) = I, опять только на Lin(Ω).

Изображения, содержащие конфигурации с более чем одним атомом, кодируются с помощью y-отображения, причем образующие обрабатываются по одной в соответствующих временных кадрах. Все это происходит точно так же, как и в случае одного атома, но здесь необходимо учитывать инерцию кодирования {см. аксиому 04). Для регулярной конфигурации с образующими g₁, g2,....,g_n получаем (см. (6.2.9))

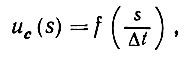(6.2.76)

где f - некоторая u-значная периодическая функция, имеющая период Δt и принимающая значения u_i = u(g_i) на интервалах длины (Δt_i)/Δt. Итак, в силу (6.2.49)

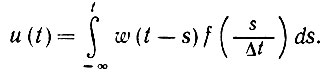(6.2.77)

Если Δt невелико (высокая скорость сканирования) по сравнению с t_c, то выражение (6.2.77) можно аппроксимировать его пределом при Δt ↓ 0. На основании теоремы Винера (см., например, Бохнер (1932)) получаем следующее:

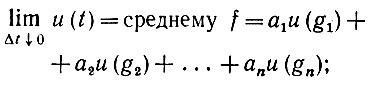(6.2.78)

это можно представить в виде отдельного предложения.

Предложение 6.2.10. Быстрое сканирование регулярной конфигурации c = (g₁ g₂, . ., g_n) порождает кодированное представление в виде вектора u, определенного в (6.2.78), причем а_i = (Δt_i)/Δt.

Другими словами, регулярные конфигурации кодируются векторами вида u(g_i), причем образующие кодируются по отдельности, так же как и их выпуклые линейные комбинации, когда вся конфигурация сканируется как единое целое. Это обстоятельство имеет важные последствия с точки зрения возможностей обучения и мыслительных способностей Ω.

После того как конфигурация с закодирована, например, в виде u(c), снова производится уплотнение - полное или частичное. Допустим для простоты, что мы имеем дело с полным уплотнением порядка m. Тогда следует обратиться к оператору опыта для Y → Y, который теперь определяется как

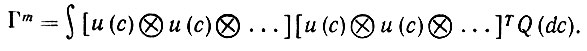(6.2.79)

Свойства Γ^m, которые мы будем записывать без верхнего индекса, если это не вызывает никаких недоразумений, вполне аналогичны его свойствам при отсутствии уплотнения.

Введем при некотором δ > 0 множество

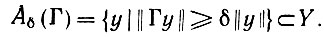(6.2.80)

Аналогично это было бы сделано в U до уплотнения. В таком случае множество Α_δ(Γ) играет роль сознания Ω, а остальные векторы образуют подсознательную часть входного пространства. Множество A_δ(Γ) не является линейно замкнутым, оно не есть некоторое подпространство Y, а образует в нем конус. Если передаточный шум u_noise отсутствует, то можно принять δ = 0.

Смысл введения (6.2.80) становится очевидным, если обратить внимание на то, что математическое ожидание оператора опыта y равно

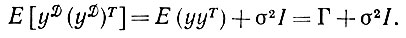(6.2.81)

Новый оператор определенный, причем все его собственные значения равны по крайней мере σ². Смысл (6.2.81) сводится к тому, что передаточный шум прибавляется к опыту Ω при помощи построения на "дне" Y собственных пространств, обладающих очень слабыми реакциями на раздражитель. Если 6 достаточно мало, то они будут являться лишь частью подсознания.

Возвращаясь к примеру, приведенному в конце разд. 6.1, мы воспользуемся следующим видом кодирования в нашем небольшом машинном эксперименте, посвященном имитации процессов мышления Ω. Рассмотрим вектор u, построенный, как описано выше, и имеющий вид

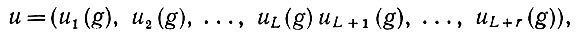(6.2.82)

где r - число используемых цветов. Тем самым мы имеем ввиду, что их соответствует локализационным признакам φ^loc_x при x = 1,2, L и u_L+j соответствует цветовым признакам φ^loc_j при j = 1,2,..., r.

Если мы хотим, чтобы Ω могло судить о наличии или отсутствии какого-то цвета или пары цветов в конфигурации, то необходимо уплотнить все uL+j попарно друг с другом. Если мы хотим, кроме того, чтобы Ω было в состоянии установить, заняты или нет две смежные позиции одновременно, необходимо уплотнить каждый их с их+1 (нижние индексы, как и раньше, берутся по модулю L). Объединив эти два условия, получаем уплотненный вектор

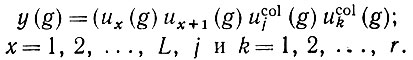(6.2.83)

Это уплотнение является частичным и имеет порядок m = 4, размерность соответствующего пространства Y равна Lr², т. е. мы имеем уплотнение довольно низкого уровня.

При распечатке векторов y время от времени в процессе моделирования возникает впечатление, что, несмотря на чрезвычайно простые среды и схемы кодирования, декодирование вектора y в некоторую образующую, исходя из интуитивных соображений, оказывается делом не простым: векторы y выглядят весьма хаотично. Это было бы справедливо даже в еще большей степени, если бы мы воспользовались для представления сенсорных входных сигналов другой системой координат.

Теперь, следуя нашей общей методе, мы можем построить исчисление высказываний для наблюдаемых объектов в данном примере. В результате мы получаем проекции, соответствующие высказываниям типа

"конфигурация с содержит вертикальную образующую";

"конфигурация с содержит горизонтальную и не содержит вертикальной образующей";

"существует конфигурация c∈exp(Ω) со смежными ненулевыми образующими".

Вопрос о том, в состоянии ли Ω на самом деле развить свою сознательную сферу в степени, позволяющей ему осуществлять вывод и рассуждать в таких категориях, будет изучен в разд. 6.4.