6.7. Сеть, функционирующая неверно

В предыдущем разделе вывод, осуществляемый Ω, рассматривался при допущении о том, что сеть работает нормально: оператор сети должен быть устойчив и, следовательно, состояние равновесия достижимо, ||N|| < χ^-1. В противном случае нельзя гарантировать, что Ω будет обучаться и реагировать на среду, как было описано.

В принципе наше существо Ω можно представить точкой (ω, N) в некотором фазовом пространстве. В данном случае ш - это вектор состояния, характеризующий кратковременную память, и N - оператор сети (долговременная память). В таком фазовом пространстве особый интерес для нас представляет нормальная область.

Определение 6.7.1. Нормальная область фазового пространства точек (ω, N) есть множество

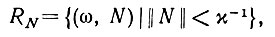(6.7.1)

а патологическая область-дополнение множества R_N.

Вне нормальной области поведение Ω будет "сумасбродным", характеризуясь бурными реакциями даже на регулярные конфигурации. При количественном анализе такого поведения нельзя больше опираться на равновесное решение (6.4.15), используемое в (6.5.1) и (6.5.2). Вместо этого в последнем уравнении ω = 2 должно быть вычислено из полного уравнения Вольтерра (6.4.7) или его аппроксимации (6.4.29).

Воспользовавшись (6.4.29) и не усредненным вариантом (6.5.2), приходим к следующей системе:

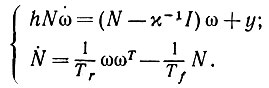(6.7.2)

В связи с тем что во втором уравнении имеется внешнее произведение, а в первом - матрично-векторное произведение (N - χ^-1I) на ω, мы имеем дело с нелинейным дифференциальным уравнением первого порядка.

Допустим на время, что на вход подается некоторый постоянный сигнал y(t) = y ≠ 0. Очевидно, что наша динамическая система (6.7.2) будет в качестве особой точки для Ω иметь (ω₀, N₀). если

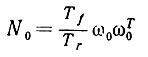(6.7.3)

и

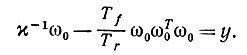(6.7.4)

Второе уравнение можно переписать,

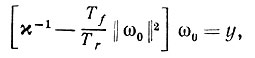(6.7.5)

учитывая, что ω₀ω^T₀ = ||ω₀||² ⋅ ω₀, и следовательно, ₀ - кратное y. таким образом, N₀ - кратное yy^T. Пусть ω₀ = xy, где x - скаляр так что уравнение (6.7.5) принимает вид

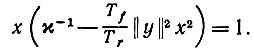(6.7.6)

Это кубическое уравнение, имеющее одно, два или три решения в зависимости от значения ||y||.

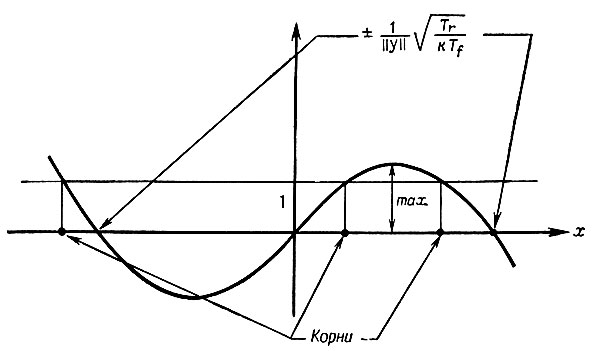
Рис. 6.7.1

Мы предполагаем, что из трех особых точек данного дифференциального уравнения асимптотически устойчива лишь наименьшая положительная. Если это действительно так, то мы должны иметь (см. рис. 6.7.1) max > 1. В точке максимума, однако,

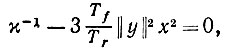(6.7.7)

и, следовательно,

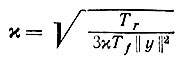(6.7.8)

и

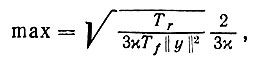(6.7.9)

так что мы получаем следующее условие (сравним с предложением 6.5.1):

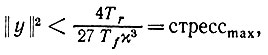(6.7.10)

Предложение 6.7.1 (гипотетическое). При постоянном входном Ω сигнале Ω будет достигать асимптотически устойчивого равновесия только в том случае, если энергия сенсорного входного сигнала меньше, стресс_max.

Таким образом, патологическое функционирование сети может быть вызвано сенсорными входными сигналами, превышающими некоторый стрессовый уровень. Другими причинами могут явиться синаптические изменения, вызванные не входными сигналами в соответствии с (6.7.2), а неправильно функционирующими нейронами. В результате могут появиться аномальные значения n_kl в χ или временных постоянных Т_r и T_f.

Допустим, что Ω достигло некоторой патологической фазовой точки -какова бы ни была причина, но при условии, что (6.7.2) все еще имеет место. Другими словами, мы ограничиваемся рассмотрением таких патологий, при которых сеть все еще подчиняется тем же самым уравнениям динамики, т. е. мы имеем дело с функциональными нарушениями. Противоположный случай - органические нарушения характеризуется другой системой уравнений, при которой сеть существенно изменяется. Какая-то часть сети может, например, оказаться разрушенной, может быть искажена кодировка g → y(g) или поражен аппарат периферийной обработки. В случае функционального расстройства нас интересует, какого рода входные сигналы должны выбираться "врачем" для того, чтобы вернуть (ω, N) в нормальную область R_N.

Самый простой вид лечения - это, естественно, изоляция Ω от сенсорных воздействий: y(t) ≡ 0 - лечение изоляцией. Особые точки уравнения (6.7.2) для этого случая можно получить путем небольшой модификации рассуждений, приводящих к предложению 6.7.1. В соответствии со вторым из уравнений (6.7.2) мы должны иметь

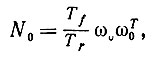(6.7.11)

и, следовательно,

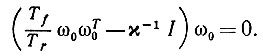(6.7.12)

Это дает особую точку ω0 = 0 и N₀ = 0. Единственная другая возможность возникает, если матрица, на которую ω₀ умножается в (6.7.12), особенная, ||ω₀||² = Т_r/χT_f и справедливо (6.7.11). Если m = 1, то появляются еще две критические точки:

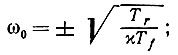
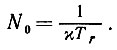(6.7.13)

Одномерный случай, естественно, не представляет почти никакого интереса, поскольку в нашем подходе особое значение придается высокой размерности. Тем не менее полезно на конкретном примере посмотреть, что на самом деле происходит, и поэтому мы проанализируем фазовый портрет дифференциального уравнения применительно к этому случаю. Интересующая нас часть плоскости (ω, N) - это верхняя полуплоскость, поскольку матрица N всегда неотрицательно определенная. Имеются три только что полученные особые точки.

Введем множества

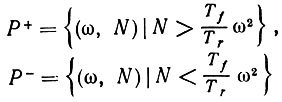(6.7.14)

и напомним, что для нормальной области R_n мы имеем 0 ≤ N < ^-1. См. рис. 6.7.2.

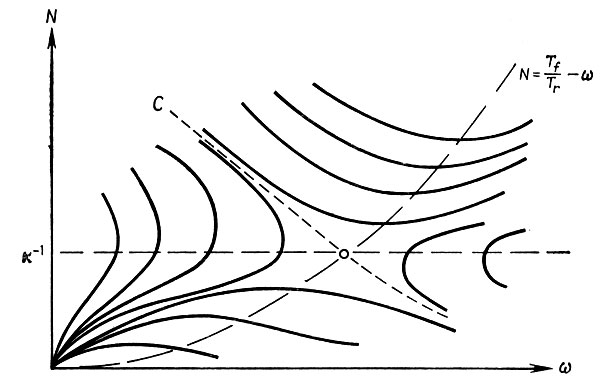
Рис. 6.7.2

Пусть для начала Ω находится в нормальной области. В условиях лечения изоляцией из уравнения (6.7.2) следует, что ω/ω отрицательно и, следовательно, со движется к нулю. Если Ω∈Р⁺, то значение N убывает, в противном случае оно увеличивается. На параболе N = (T_f/T_r)ω² оно постоянно. На границе N = χ^-1 нормальной области траектории имеют вертикальные касательные.

Если Ω∈Р⁺∩R_N^C, то со возрастает, в то время как N убывает, и это продолжается до тех пор, пока траектория не достигает границы этого пересечения: либо N = χ^-1, когда Ω переходит в нормальную область, либо парабола, когда Ω все еще находится в патологической области, но передвигается к P^-.

Если Ω∈Р^-∩R_N^C то и ω, и N возрастают. Объединяя эти результаты, получаем качественный фазовый портрет; он изображен на рис. 6.7.2. Одна особая точка находится в начале координат, другая, задаваемая (6.7.13),- это седло. Следовательно, "история болезни" Ω при лечении изоляцией будет зависеть от того, находится ли начальное значение на фазовом портрете выше кривой С или нет. Итак, можно сформулировать следующее предложение.

Предложение 6.7.2.При m = 1 лечение изоляцией обеспечит возвращение Ω в нормальную область, если текущая позиция в фазовом пространстве находится ниже С. В противном случае это лечение не даст желаемого результата.

Если Ω пребывает выше С, то рекомендуется активное лечение, y ≠ 0. Как же "врач" должен выбирать сенсорную входную функцию у, если допустить, что он волен выбирать любую функцию, которую пожелает? Если цель заключается, например, в том, чтобы вернуть Ω в некоторую точку, скажем ω = 0, W =0, то необходимо решить N^⋅/ω^⋅ = -N/ω относительно y. Используя (6.7.2) путем непосредственного вычисления получаем

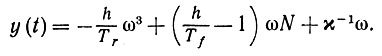(6.7.15)

Другая стратегия лечения могла бы заключаться в том, чтобы добиваться достижения границы нормальной области, сохраняя ω постоянным. Это приводит к следующей сенсорной входной функции:

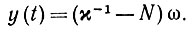(6.7.16)

Такой способ будет действовать только тогда, когда Ω∈Р⁺ поскольку в противном случае N растет и переводит Ω в еще худшие состояния.

Возвращаясь к общему случаю размерности m, можно поставить вопрос о стратегиях лечения, обеспечивающих возвращение Ω к нормальному функционированию, что связано с некоторой сенсорной входной функцией y(t). Может оказаться, однако, что необходимо использовать некоторое значение y₀, такое, что y₀∉Y(exp(Ω)), и, следовательно, в опыте Ω нет никакой регулярной конфигурации, соответствующей данному входному значению.

В таком случае мы вынуждены выйти за пределы Y(exp (Ω)), и если y₀∈Y(env (Ω)), то это означает, что врач предложит Ω конфигурацию у которая регулярна, но не принадлежит "нормальному" опыту Ω.

Если же y₀ не входит даже в Y (env (Ω)), то врач должен искусственно создать представление y₀, быть может, с помощью лекарств или гипноза.

Кроме подобных ограничений на допустимые значения у при лечении могут существовать ограничения типа ||y||² ≤ const, ограничивающие энергию на входе, или ∫||y||²dt ≤ const. Допустим, что врач должен ограничиваться y(⋅) ∈ F и ω(t₀) = ω₀, N(t₀) = N₀; в таком случае можно сформулировать в общем виде задачу оптимального лечения функциональных нарушений.

Требуется найти y(⋅) ∈ F такой, чтобы время T за которое (ω(t), N (t)) впервые достигает R_n было минимальным. Эта задача относится к теории управления, и поэтому естественно попытаться установить, применим ли к ней принцип импульсного управления Ласалля.

Анализ функциональных нарушений, проведенный в данном разделе, имеет лишь предварительный характер. Тем не менее, судя по всему, он открывает новую перспективную область теории процессоров образов, которая, как мы надеемся, станет предметом значительно более глубоких исследований.

В связи с этим возникает и следующая проблема. При диагностике расстройства, возникающего у Ω, необходимо решить, можно или нет получить информацию о сети 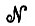на микроуровне. Если нет, то для диагностики придется обратиться к пробным образцам - конфигурациям, выбранным из алгебры изображений, - и изучать соответствующую реакцию, например энергию ||ω||² или энергию ||Θω||² каких-то выходных операторов Θ.

Тогда необходимо сформировать некоторое множество пробных образцов так, чтобы наблюдаемые результаты были полезны с точки зрения диагноза. Эта задача также относится к выводу образов, но это совершенно не тот вывод, который осуществляет Ω, находясь один на один со своей алгеброй изображений среды.