6.6. Вывод алгебры изображений

Для упрощения анализа начнем, как обычно, с одноатомных изображений, а расширение на многоатомный случай обсудим позже.

Рассмотрим теперь сеть с насыщенным и устойчивым отображением памяти, на которую воздействует входной сигнал y. Пусть C₁ - некоторое высказывание, инициированное y, так что Р(С₁)y ≠ 0. Если результирующий вектор Р(С₁) у вводится в сеть , то мм получаем сознательный ответ

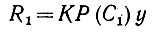(6.6.1)

в соответствии с предложением 6.4.1. Если, с другой стороны, у инициирует некоторое другое высказывание С₂, то ответ сети будет

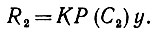(6.6.2)

Может оказаться, что ответы R₁ и R₂ абсолютно не связаны, т. е. R₁ ⊥ R₂. Сеть совершенно по-разному реагирует на векторы P(C₁)y и Р(С₂)y. С другой стороны, может оказаться, что внутреннее произведение (R₁, R₂) ≠ 0, т. е. реакции имеют нечто общее между собой. В результате возникает следующая формализация идеи обучения.

Определение 6.6.1.(i) будем говорить, что входной вектор у инициирует связь между двумя высказываниями С₁ и С₂, если

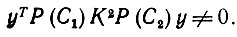(6.6.3)

(ii) Мы будем говорить, что входной вектор у обеспечивает запоминание существом Ω высказывания С, если он инициирует возникновение связи с самим собой:

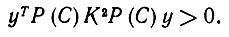(6.6.4)

Будем говорить, что сеть установила посредством обучения связь между высказываниями и С₂, если существует входной вектор, инициирующий эту связь. Аналогично мы говорим, что высказывание C установлено посредством обучения, если существует вектор y, обеспечивающий запоминание сетью высказывания C.

Следовательно, Ω обучается связывать С₁ и С₂, если P(C₁)K²P(С₂) ≠ 0, и обучается С, если Р(С)К ≠ 0.

Это качественное определение можно превратить в количественное, заменив (6.6.3) и (6.6.4) величинами

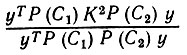(6.6.5)

и

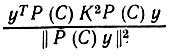(6.6.6)

соответственно.

Обучение, таким образом, представляется изменением геометрии с внутренним произведением, связанным с матрицей K. Здесь речь идет не о геометрии физического пространства, в котором расположена сеть но об ω-пространстве с новой геометрией.

Что же можно сказать относительно способностей Ω к обучению, если задана структура образов env (Ω)? Очевидно, во-первых, что достижимый уровень обучения зависит не только от env (Ω) - потенциальной среды Ω. Здесь играет роль также частота (и продолжительность) предъявления различных объектов. Другими словами, именно опыт exp (Ω) определяет, какие понятия будут сформированы в результате обучения, а какие нет.

Сформулируем это более точно.

Предложение 6.6.1. Существо Ω обучится высказыванию С, если оно реализовано в exp (Ω).

Доказательство. Если в exp (Ω) имеется образующая g, для которой С (g) = ИСТИНА, то из предложения 6.2.7 следует, что Р (С) инициирует y(g). Это означает, что подпространство сознательной сферы Γ будет содержать элемент Р(g)y. Неформально это означает, что Γ будет получать вклад ΔΓ, пропорциональный y(g)y^T(g), и, следовательно, y^T(g)Р(С)ΔΓP(С)y(g) пропорционально

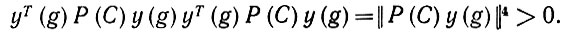(6.6.7)

Операторы Γ, N, K и K², однако, имеют одно и то же ядро. Следовательно, неравенство (6.6.4) справедливо при y = y(g) и Ω обучилось С.

Если С -аналитическая ИСТИНА, то Р (С) - единица, так что Р(С)K = K > 0 и, следовательно, Ω наверняка обучается понятиям, которые аналитически истинны.

Справедливо частичное обращение этого предложения.

Предложение 6.6.2. Существо Ω обучится некоторому высказыванию С только тогда, когда оно реализуется в exp (Ω), расширенном так, что в него входят фиктивные объекты разд. 6.2.

Доказательство. Допустим, что высказывание С сформулировано посредством обучения, так что существует некоторый вектор у, удовлетворяющий условию (6.6.4). Отсюда следует, что

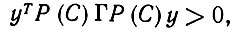(6.6.8)

и, таким образом, Р(С)y имеет ненулевую проекцию ух в подпространство сознательной сферы Γ. Вектор y₁ однако, будет принадлежать Lin[exp(Ω)] и, следовательно, представляет некоторый объект в exp (Ω) или некоторый фиктивный объект, который в обоих случаях удовлетворяет С.

Предложение 6.6.3.Если высказывания C₁ и С₂ одновременно реализованы в exp (Ω), то Ω научится связывать С₁ и С₂.

Доказательство. Допустим, что Ω не обучилось установлению этой связи и, следовательно,

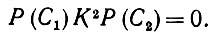(6.6.9)

Напомним, что R(С₁), Р(С₂), K, N и Γ получены как неотрицательные комбинации ряда элементарных операторов проектирования. Тогда из (6.6.9) следует, что

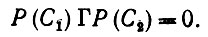(6.6.10)

Поскольку, однако, Г построен и" вкладов типа y(g)y^T(g), g∈exp(Ω), то должно иметь место

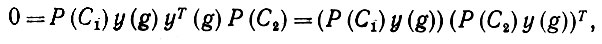(6.6.11)

причем здесь внешнее произведение равно нулю только тогда, когда

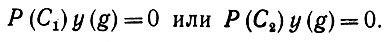
Отсюда следует, что конъюнкция

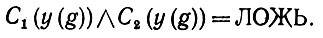(6.6.12)

Это означает, что С₁ и С₂ не могут быть одновременно справедливы в ехр(Ω), и, таким образом, предложение доказано.

В этом анализе решающую роль играет оператор K, а через него - оператор опыта Γ. Напомним -обсуждение, проведенное в конце разд. 6.2, показало, что можно ожидать либо почти ортогональности, либо почти пропорциональности входных векторов y. Первый случай соответствует действительно различным объектам, второй -почти "тому же самому" объекту, подвергнутому преобразованиям подобия.

Пусть Γ имеет собственные значения γ₁, γ₂, ... с соответствующими нормированными собственными векторами V₁, _V2, ... .Примем для простоты, что собственные значения простые; в противном случае последующее изложение потребует модификации,

но несущественной. Пусть на вход поступил вектор y, и, следовательно, оператор приращения опыта равен

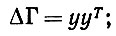(6.6.13)

тогда очевидно, что если y = CV_r, то единственное изменение Γ состоит в том, что γ_r заменяется на γ_r + C². Подобным же образом, если y ортогонален всем V_r, Γy = 0, то Γ приобретает некоторый новый собственный вектор y с собственным значением ||Y||². Если ввести пучок векторов y, близких друг к другу и таких, что

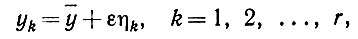(6.6.14)

где

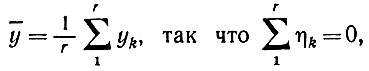(6.6.15)

то мы получаем оператор приращения опыта

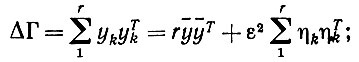(6.6.16)

здесь мы воспользовались тем фактом, что сумма η равна нулю. Если ȳ - это "старый" собственный вектор V_r, а η ортогональны Γ, то из (6.6.16) следует, что Γ изменяется в двух отношениях. Его собственное значение Vr увеличивается до V_r + r²||y||₂, а также затрагиваются очень малые собственные значения порядка ε². Последнее скажется лишь на "дне" пространства, соответствующем низкому уровню сознания. Иначе говоря, мы приходим к следующему предложению.

Предложение 6.6.4.Если exp (Ω) образован из истинно различных объектов, к которым применяются различные преобразования подобия, то приближениями собственных векторов оператора опыта являются y(g), где значениями g служат неподобные прототипы из exp(Ω).

Отметим, что объекты среды (приближенно) представлены как собственные векторы оператора K. На дне подпространства сознательной сферы Γ и К можно обнаружить эффект, вызванный применением различных преобразований подобия к объектам. Он будет разделять это пространство с эффектами, вызванными передаточным шумом и шумом основного процессора . Соответствующие собственные значения характеризуют энергию входного вектора, продолжительность предъявления и вероятность выбора объектов.

Нетрудно распространить вышеуказанное на случай более точной аппроксимации. В самом деле, если добавить к Γ приращение ΔГ = εyy^T, скажем, при y = V_r, то можно воспользоваться для вычисления изменения y_r стандартным методом возмущений. В результате получаем новое собственное значение

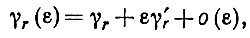(6.6.17)

где

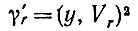
и изменение собственного вектора можно вычислить аналогично. Читателю, интересующемуся подробностями, следует обратиться к монографии Рисса и Надя (1952), гл. IX.

Предложение 6.6.4 имеет одно забавное следствие. Пусть объекты g₁, g₂,....,g_n предъявляются по одному. Существо Ω обучится соответствующим одноатомным изображениям I₁, I₂, ..., формируя ортогональные подпространства и строя в них проекции, принадлежащие изображениям. Если эти объекты совершенно различны, то все прекрасно. Если же какие-либо из них сходны друг с другом, то нам известно, что соответствующее подмножество объектов порождает в сознательном подпространстве только один собственный вектор. Так будет происходить по крайней мере в течение некоторого времени, и для того, чтобы Ω обучилось всем объектам, потребуется более длительное предъявление. Итак, сходство объектов будет замедлять процесс обучения.

Предложение 6.6.5. Рассмотрим изображения в = env(Ω). состоящие в каждый момент времени из одной образующей g₁, g₂, ..., так что их векторы у имеют единичную норму. Пусть Т-время:, необходимое для обучения всем g в том смысле, что все n собственных векторов, соответствующих ΔΓ, подняты до уровня δ, тогда Т принимает минимальное значение, когда все y(g_k) взаимно ортогональны.

Доказательство. Если y(g_k) ортогональны, то предъявление Ω изображения I в течение Т единиц времени дает

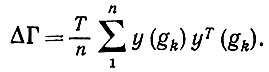(6.6.18)

Если y(g_k) ортогональны, выбираем систему координат так, что k-я компонента y_k равна 1, а остальные 0. Тогда ΔΓ, суженный на соответствующее n-мерное подпространство, представляет собой единичный оператор, взятый Т/n раз в этом подпространстве. При этом все собственные значения ΔΓ равны Т/n, и чтобы обучиться изображению в указанном выше смысле, требуется время предъявления (nδ)/Т. Допустим теперь, что y(g_k) уже не ортогональны, о все еще имеют единичную длину. В таком случае неотрицательно определенный оператор приращения опыта ΔΓ еще удовлетворяет условию tr(ΔΓ) = T, означающему, что его наименьшее собственное значение самое большее равно Т/n. Следовательно, для обучения требуется время предъявления по крайней мере (nδ)/Т.

Пусть, например, n = 2 и два вектора y образуют угол φ. Тогда для двумерного подпространства ΔΓ можно записать, что

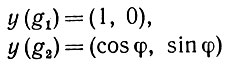(6.6.19)

и, следовательно,

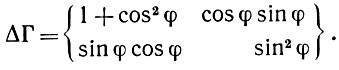(6.6.20)

Непосредственное вычисление дает для наименьшего собственного значения

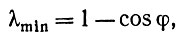(6.6.21)

так что время предъявления должно быть увеличено на коэффициент (1 - cosφ)^-1.

В данном разделе мы пренебрегаем экспоненциальным затуханием коэффициентов связи, которое характеризуется временной постоянной T_f. Это приближение справедливо лишь, когда интервалы времени существенно короче, чем Т. Следует также выяснить, что происходит в случае более продолжительных временных интервалов, но здесь мы не станем заниматься этим.

Давайте теперь расстанемся с одноатомным случаем. Если в конфигурации имеется несколько образующих, то большая часть изложенного в данном разделе остается в силе лишь с небольшими изменениями. Вклад ΔΓ в оператор опыта можно подсчитать для конфигурации, учитывая то обстоятельство, что образующие имеют когерентную кодировку. Тогда математическое ожидание равно умноженному на V выражению, зависящему Σa_ry(g_r) аналогично полученному нами для одноатомной конфигурации и зависящему от y(g). Такую линейную композицию входных векторов нельзя было бы получить, если бы кодирование было не когерентным, и тогда ΔΓ представлял бы собой сумму ΔΓ_r, причем каждый ΔΓ_r определялся бы одной из образующих конфигурации. В последнем случае Ω не могло бы обучиться никаким связям между объектами. Таким образом, условие когерентности является критическим.

Следует подчеркнуть, что, поскольку должно быть обеспечено Δt ≤ t_c и Δt_i ≥ t_scan, то, следовательно, при n = # (объектов) мы получаем неравенство

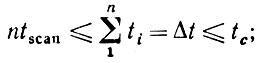(6.6.22)

таким образом, получено неравенство для числа объектов, которые можно хранить в краткосрочной памяти:

(6.6.23)

Следовательно, краткосрочная память может содержать самое большее n_max объектов одновременно.

Предложение 6.6.6.Сеть 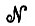может содержать в своей краткосрочной памяти самое большее n_max объектов; n_max определяется из (6.6.23).

Это обстоятельство повлияет на способности Ω к обучению, так как модификация отображения памяти, построенного оператором К, осуществляется через равновесное состояние вектора о.

Остановимся теперь на некоторых существенных ограничениях способности Ω к обучению. Мы убедились в том, что оно может обучаться понятиям, соответствующим проекциям в Lin (#(ехр (Ω)). При изучении одноатомных конфигураций мы отметили, что из этого следует также возможность обучения Ω фиктивным объектам. Это зависит от того, является ли множество y(exp (Ω)) линейно замкнутым или нет. При переходе к многоатомным конфигурациям мы знаем, однако, что векторы y объединяются путем сложения, и в связи с вариацией u₀ создается впечатление, как будто бы фиктивные объекты (если таковые имелись) могли быть отождествлены с конфигурациями объектов.

Это не обязательно так. Во-первых, как указывалось в разд. 6.1, понятие образующей включает свойства, которые могут зависеть от других объектов. Две образующие g₁ и g₂ не всегда можно объединять (должны выполняться условия регулярности 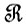, так что упомянутое множество y не обязано быть линейно замкнутым, и мы не можем пренебрегать фиктивными объектами при любых обстоятельствах. Во-первых, как мы убедились в разд. 6.2, построение линейного замыкания посредством вариации значений u₀ предусматривает не когерентное кодирование. Это противоречит аксиоме 01, и, следовательно, фиктивные "объекты" не всегда могут интерпретироваться как конфигурации, состоящие из нескольких объектов.

Другое ограничение возникает в случае неполного уплотнения. Допустим, что одновременно уплотняются лишь μ из U^υ - пространств, μ < r, где r - число сенсорных подпространств U. Соответствующая иллюстрация приведена на рис. 6.6.1, где линии передачи от U^υ и U^υ' к Y^υυ' представляют собой кабели, каждый из которых содержит несколько отдельных жил, r = 3, μ = 2. Мы буем называть такое уплотнение - дробным μ/r.

Тогда мы имеем r(r - 1).. . (r - p + 1) подпространств Y^υυ'. Если, например, все U^υ имеют размерность d, то объединенное

пространство Y будет обладать размерностью

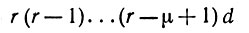(6.6.24)

вместо размерности d^r соответствующей случаю полного уплотнения. Это сравнение несколько некорректно, поскольку мы воспользовались в (6.6.24) симметрией с тем, чтобы сократить размерность. Так, например, на рис. 6.6.1 Y₂₁ отсутствует, поскольку его обязанности с тем же успехом может выполнить Y₁₂. Подобная экономия может быть обеспечена и в случае полного уплотнения, что дает приблизительно половинную размерность. Уменьшение, обеспеченное дробным уплотнением, характеризуется множителем

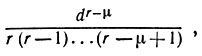(6.6.25)

входящим в выражение, определяющее полную размерность пространства входных сигналов, которая может быть очень велика.

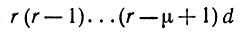
Рис. 6.6.1

Дробное уплотнение имеет одно интересное следствие. Если воспользоваться в качестве модели конъюнкциями простых высказываний, то одновременно мы можем работать с конъюнкциями самое большее μ простых высказываний. Обращение к логике признаков, рассмотренной в разд. 6.1, позволяет сформулировать такое предложение.

Предложение 6.6.7.Если дробное уплотнение μ/r используется для передачи сенсорной информации в сеть, то Ω может обучиться только тем высказываниям, которые принадлежат логике признаков порядка μ.

Следовательно, могут существовать правильно построенные высказывания в exp (Ω), которым, несмотря на их истинность, Ω никогда не сможет обучиться.

В крайнем случае μ = 1, т. е. при уплотнении 1/r, что на самом деле означает просто отсутствие уплотнения, мы вообще не сможем работать с конъюнктивными высказываниями. Так, например, высказывание, утверждающее, что какая-то образующая g обладает предикатами "БОЛЬШОЙ" и "СИНИЙ" одновременно, недоступно Ω, поскольку оно не соответствует ни одному из его проектирующих операторов.

Разумеется, это препятствие можно обойти, рассматривая осознание Ω конъюнктивного высказывания как овладение вначале предикатом "БОЛЬШОЙ" и немедленно после этого предикатом "СИНИЙ". В принципе это отличается от нашего подхода, при котором высказывания, осознаваемые Ω, имеют непосредственную интерпретацию как некий единый оператор. Мы стремились к достижению полного соответствия между мышлением Ω и операторами, ассоциированными с сетью. При таком подходе уплотнение необходимо для того, чтобы наделить Ω способностью к нетривиальному выводу структуры образов его среды.

Предложение 6.6.4 показывает, что y-отображения различающихся образующих не должны быть вполне ортогональны для того, чтобы обучение описанного типа имело место. Чем больше размерность пространства Y, тем вероятнее, что приближенно ортогональность будет выполняться (см. предложение 6.2.4 и его непосредственные следствия). Для того чтобы установить точнее, чего можно ожидать, рассмотрим некоторое количество m векторов y, случайно выбранных из n-мерного пространства, и изучим, как влияет размерность n на обучение и установление ассоциаций. Обращаем внимание на то, что обозначения, используемые здесь, отличаются от употреблявшихся выше. Справедливо следующее предложение.

Предложение 6.6.8.Если векторы у порождаются статистически независимо, причем каждый из них подчиняется нормальному распределению с нулевым средним и ковариационной матрицей (1/n)I, то получаемый в результате оператор опыта обладает свойствами:

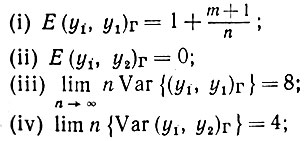
здесь (u, υ)_Γ обозначает внутреннее произведение u и υ в соответствии с геометрией, определяемой оператором опыта.

Доказательство. Доказательство элементарно, но требует рассмотрения различных случаев. Для произвольных векторов n и υ

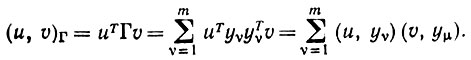(6.6.26)

Отметим, что в этом предложении речь идет о вариациях в обучении, вызванных вариациями раздражителей y_υ, т. е. о влиянии в долгосрочном смысле.

Доказательство (i). Так как

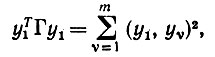(6.6.27)

то в первую очередь необходимо вычислить

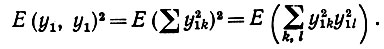(6.6.28)

Отсюда, однако, разделив диагональные и недиагональные элементы и учитывая, что Е(y⁴) = 3, мы непосредственно получаем

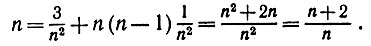(6.6.29)

С другой стороны, члены типа

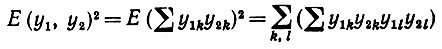(6.6.30)

дают вклад

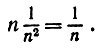(6.6.31)

Следовательно,

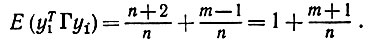(6.6.32)

Доказательство (ii). Здесь мы имеем дело с выражением

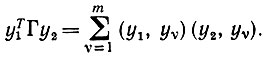
При суммировании выделяются три случая: υ = 1, 2 и другие значения. При υ = 1 получаем

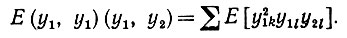(6.6.33)

Поскольку, однако, y_n не зависит от остальных множителей, то эта сумма обращается в нуль. Аналогично при υ = 2. Если же υ = 1 и ≠ 2, то необходимо вычислить

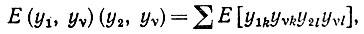(6.6.34)

что дает просто нуль.

Доказательство (iii). Для определения дисперсии нам требуется значение

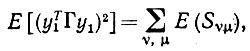(6.6.35)

где

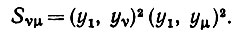(6.6.36)

В общем случае имеем разложение

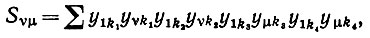(6.6.37)

где суммирование проводится по k_i = 1,2, ..., n.

Чтобы определить математическое ожидание подобных одночленов восьмой степени, мы воспользуемся тем, что для нормально распределенных случайных величин с нулевым средним значением

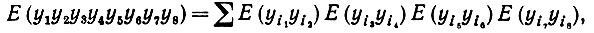(6.6.38)

где суммирование проводится по всем различным комбинациям восьми индексов в пары. Мы рассмотрим четыре разновидности членов, входящих в (6.6.36) (см. табл. 6.6.1, где представлены эти типичные случаи). В частности, случай II заключается в том, что один индекс равен единице, другой - отличается от единицы и т. д.

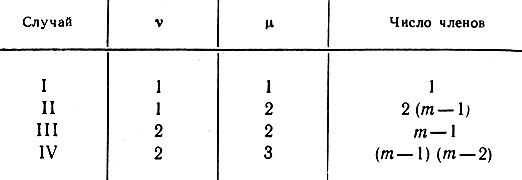
Таблица 6.6.1

Случай I: υ = 1, μ = 1. Здесь, используя (6.6.37), можно записать следующее:

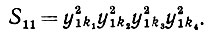(6.6.39)

Для того чтобы получить математическое ожидание этой величины, мы снова рассмотрим отдельные случаи. Вклад, соответствующий всем различным k, определяется так:

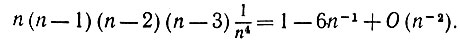(6.6.40)

Если k₁ = k₂ отличаются от k₃ = k₄, то соответствующий вклад равен

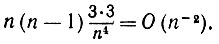(6.6.41)

Аналогичный результат получается при k₁ = k₂ отличающихся от k₂ = k₁ и т.д. Нам не потребуется повторять эту подстановку позже, если порядок составляет n^-3 или меньшую величину. Если k₁ = k₂ = k₃ отличаются от k₄, то, поскольку E(y⁶) = 15, мы получаем

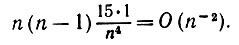(6.6.42)

Если k₁ = k₂ = k₃ = k₄, то, поскольку E(y⁸)= 105, мы получаем

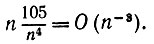(6.6.43)

Если все k₁, k₂, и k₃ различные и k₃ = k₄, то мы получаем

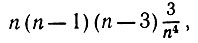(6.6.44)

и сделано это может быть шестью различными способами. Тогда основной член общего вклада получается путем суммирования (6.6.40) и умножения (6.6.44) на 6, что дает в результате

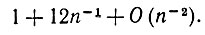(6.6.45)

Очевидно, что ведущие члены будут соответствовать случаю, когда число различающихся k максимально велико, так что возникают ненулевые члены

Случай II: υ = 1, μ = 2, и, следовательно,

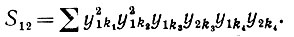(6.6.46)

Если все k различны, то математическое ожидание одночлена равно нулю. Если k₁ = k₂ отличаются от k₃ = k₄, то соответствующий вклад в S₁₂ равен

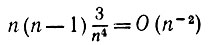(6.6.47)

и т. д. Если k₁, отличается от k₂ = k₃ = k₄, то мы получаем

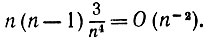(6.6.48)

Если все k_i одинаковы, то мы получаем лишь

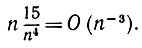(6.6.49)

Если k₃ = k₄ и все k₁, k₂ и k₃ разные, то мы имеем

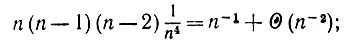(6.6.50)

таким образом, этот вклад и является основным членом S₁₂.

Случай III: υ = μ = 2, и, следовательно,

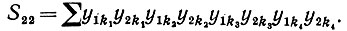(6.6.51)

Когда все k различны, мы получаем нуль. Если k₁ = k₂ отличаются от k₃ = k₄, то мы имеем

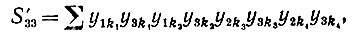(6.6.52)

Когда все k одинаковы, мы получаем О(n^-3). Полный вклад в данном случае O(n^-2).

Случай IV: υ = 2, μ = 3, и, следовательно,

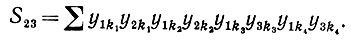(6.6.53)

Прибегая к тем же рассуждениям, убеждаемся, что математическое ожидание S₂₃ равно O(n^-2).

Объединяя эти результаты, мы получаем (см. табл. 6.6.1) и пункт (i) предложения 6.6.8):

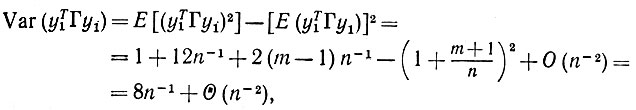(6.6.54)

что и доказывает утверждение (iii) предложения 6.6.8.

Доказательство утверждения (iv). Рассмотрим пять случаев, указанных в табл. 6.6.2, причем случай V' предусматривает, что υ = μ = 1 или = 2.

Уравнение (6.6.37) следует теперь заменить следующим уравнением:

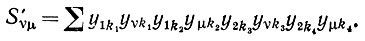(6.6.55)

Случай I': υ = 1, μ = 2, следовательно,

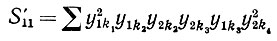(6.6.56)

и

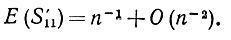(6.6.57)

Случай II': φ = 1, μ = 3, и, следовательно,

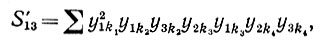(6.6.58)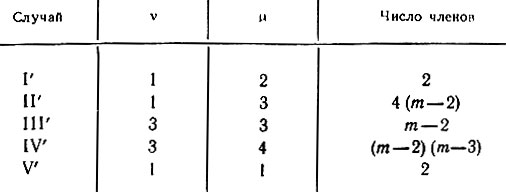

Таблица 6.6.2

Случай III': υ = μ = 3, и, следовательно,

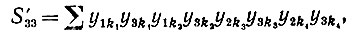(6.6.59)

а математическое ожидание ∼О(n^-2).

Случай IV': υ = 3, μ = 4, и, следовательно,

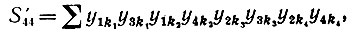(6.6.60)

а математическое ожидание ∼О(n^-2).

Случай V': υ = μ = 1, и, следовательно,

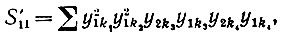(6.6.61)

а математическое ожидание равно n^-1 + O(n^-2). Объединяя эти результаты, мы получаем, что

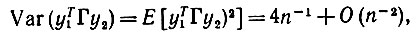(6.6.62)

на чем и заканчивается доказательство предложения 6.6.8.

Чтобы обучение имело место, необходимо ввести условие, заключающееся в том, чтобы (y₁, y₁)_Γ было существенно больше, чем (y₁, y₂)_Γ (вспомним определение 6.6.1 и отношение между K и Γ). Мы предполагаем, что m фиксировано при n → ∞, но асимптотика сохраняется до тех пор, пока m = O(√n), поскольку число членов S_υμ и S'_υμ равно m². Это соотношение будет тогда справедливо с весьма высокой вероятностью при условии, что n выбирается достаточно большим для того, чтобы выполнялось

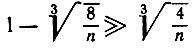(6.6.63)

(среднее значение ±3 × средние квадратичные отклонения), т. е. √n >> 14,5. Если мы хотим добиться, чтобы соотношение между левой и правой частями (6.6.63) было равно по крайней мере, скажем, 10, то n должно выбираться порядка 5000 или более; эта величина очень мала по сравнению с размерами реальных нейронных сетей.

Итак, мы приходим к выводу, что обучение будет иметь место уже при умеренных значениях n, если число m существенно различных объектов в среде пренебрежимо мало по сравнению с размерностью входного пространства.

Полученное нами значение n отражает очень пессимистическую оценку. Вероятно, даже меньшие значения п достаточны для адекватного обучения, но точнее это сформулировать трудно.

В вычислительном эксперименте, описанном в разд. 6.1 и 6.2, мы имели n = 60, что совершенно недостаточно для случая высокой размерности, т. е. условий предложения 6.2.4 и 6.6.8, но вполне достаточно для иллюстрации того, каким образом существо Ω может выводить некоторую часть структуры образов в простой ситуации.

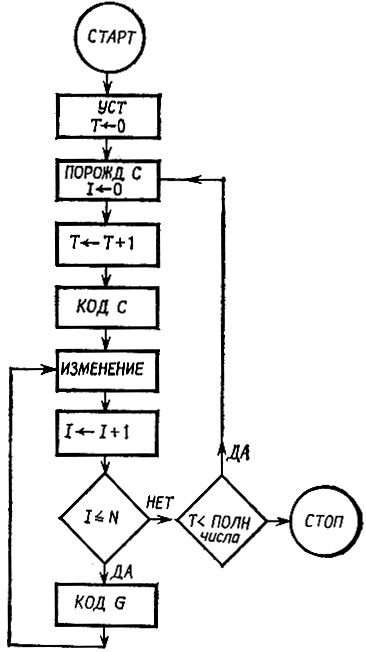
Рис. 6.6.2

Блок-схема модели процесса обучения Ω приведена на рис. 6.6.2. Блок "УСТ" инициализирует оператор сети N и устанавливает счетчик Т (число итераций) на нуль. Блок "ПОРОЖД С" порождает, как описано в разд. 6.1, одну регулярную конфигурацию и устанавливает на нуль счетчик I (число образующих в конфигурации). Далее блок "КОД С" кодирует с в целом с уплотнением, как это описано в конце разд. 6.2 (см. (6.2.83)), а блок "ИЗМЕНЕНИЕ" модифицирует N в соответствии с правилами, необходимыми для обучения. Сканируя образующие, входящие в конфигурацию, блок "КОД G" кодирует каждую из них и снова модифицирует N. Это означает, что Ω изучает кон-фигурацию в целом, а затем каждую из ее образующих. Когда значение Т становится равным общему числу порожденных конфигураций, алгоритм заканчивает работу.

Реализация этого алгоритма на языке АПЛ при различных значениях параметров показала, что обучение происходит довольно быстро: достаточным оказывается изучение от 50 до 150 конфигураций. Норма ||N|| при этом существенно нарастает, так же как и нормы ЦРМРЦ и ||PN²P|| соответствующего оператора проектирования Р.

Рассмотрим в качестве примера следующую конфигурацию:

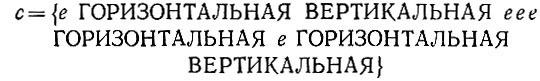(6.6.64)

(е обозначает пустую образующую) и воспользуемся проекцией, соответствующей высказыванию

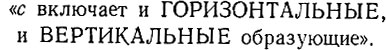(6.6.65)

Полученная в результате энергия равна 20, 89, в то время как применение этой ее проекции к конфигурации

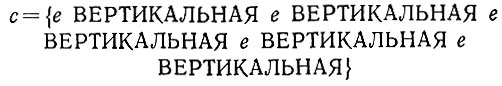(6.6.66)

проводит к энергии, равной 4,10"10. Эта энергия не равна строго нулю из-за передаточного шума, наличие которого предполагалось при кодировании.

Проекция высказывания

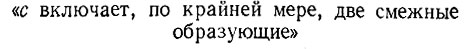(6.6.67)

приводит к энергии, равной 5348 для конфигурации (6.6.64) и всего лишь 3,7×10^-4 для

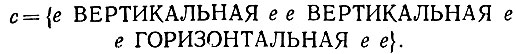(6.6.68)

Очевидно также, что N-норма 5348 последнего оператора много больше, чем N-норма 2,089 первого оператора. Вероятно, это объясняется тем, что структура образов имеет тенденцию чаще удовлетворять (6.6.67), чем (6.6.65).

Результаты моделирования представляют собой как раз то, чего можно было ожидать от нашего анализа. Интереснее, быть может, посмотреть, чему Ω не обучилось. Рассмотрим высказывание, которое не поддалось Ω при обучении:

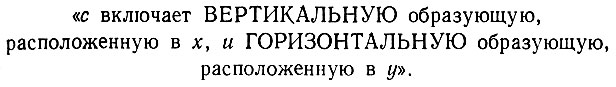(6.6.69)

При неполном уплотнении, которое было использовано в модели, Ω не имеет доступа к проекции, точно соответствующей (6.6.69). Оно не может научиться выводу на этом уровне логики признаков, и аналогичная ситуация наблюдается с многими другими высказываниями типа (6.6.69).

Естественно, Ω имеет доступ к проекции, соответствующей высказыванию "с включает по крайней мере одну ВЕРТИКАЛЬНУЮ образующую" или высказыванию "с имеет образующую, расположенную в x" и т. п. Этого, однако, недостаточно, чтобы обеспечить обучение высказыванию (6.6.69): мы настаиваем на том, что операторы точно соответствуют высказываниям. Для достижения этой цели потребовалась бы более высокая степень уплотнения, чем использованная в машинном эксперименте.

Объем вычислений, оказавшийся необходимым в этом эксперименте, умеренный - всего несколько минут работы центрального процессора. Более обширный машинный эксперимент потребовал бы, конечно, больше времени; затраты времени центрального процессора растут быстро, поскольку число коэффициентов связи имеет порядок m² (m -число нейронов). При использовании вычислительной машины с высоким уровнем параллелизации можно было бы провести моделирование для больших значений m, однако, и в этом случае создается впечатление, что реальные значения m полностью остаются за пределами возможностей реализуемых моделей.

Машинный эксперимент - это ценный, быть может, даже незаменимый инструмент изучения функционирования сети, позволяющий нам устанавливать, что именно происходит в небольших сетях, и помогающий работе нашей интуиции. Но для более глубокого проникновения в эту проблему следует обратиться к математическому анализу.

Конечно, нет необходимости постулировать для структуру полного графа. Как раз наоборот - можно допускать существование некоторой статистической топологии, как это делалось в разд. 6.2. Это приведет к структурам сети типа приведенной на рис. 6.6.3, где m = 35 и h_max = 9. Требования к памяти, а также ко времени работы центрального процессора в этом случае резко снизятся, что позволит работать с большими сетями, быть может, с m = 10 000. Но даже и при этом математический анализ является единственной возможностью добиться лучшего понимания количественных аспектов функционирования подобных идеализированных нейронных сетей, поскольку машинные эксперименты были бы чрезвычайно дороги, если вообще возможны.

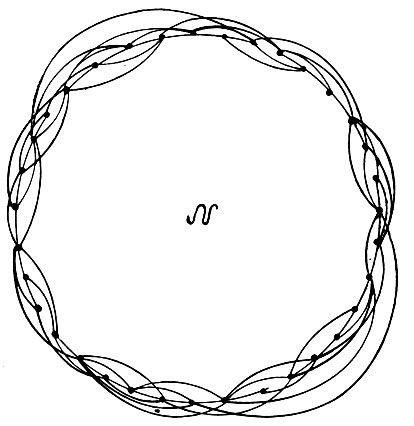
Рис. 6.6.3