7.2. Абдукция некоторых языковых образов

Исходя из общих положений предыдущего раздела, мы попытаемся теперь сконструировать алгоритмы абдукции применительно к случаю, когда образы принадлежат некоторому формальному языку. Это будет конкретным примером того, как вывод, основанный на деформациях, может быть осуществлен в рамках случая 7.1.2.

Прежде чем решить, какой тип формального языка мы будем использовать, остановимся кратко на информационном потоке, возникающем в процессе абдукции. Существо Ω (источник речи) живет в среде, которая характеризуется некоторой алгеброй изображения env(Ω) (см. рис. 7.2.1). Заданное изображение I∈env (Ω) может породить множество различных предложений, принадлежащих языку L (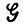), который описывается некоторой грамматикой ?. Это означает, что процессор изображений отображает алгебру изображений env (Ω) в некоторую другую алгебру изображений, так что оператор изображений, "преобразователь",представленный на этом рисунке, переводит изображения микромира в языковые изображения.

Пример работы такого оператора изображения можно найти в разд. 2.4. Как уже указывалось, отображение многозначно, поскольку некоторое заданное изображение I, принадлежащее env(Ω), может породить множество синтаксически правильных предложений, соответствующих грамматике 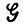и согласующихся с изображением I семантически.

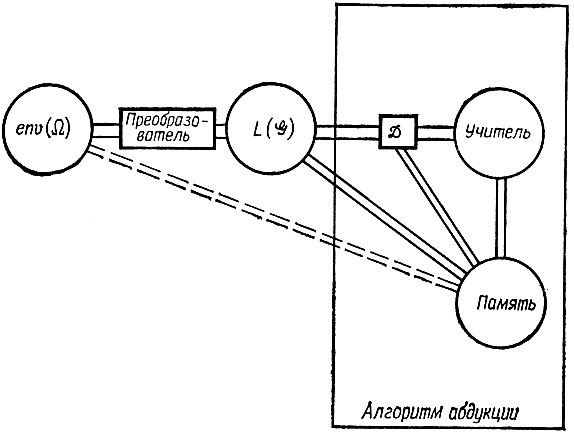
Рис. 7.2.1

Затем предложения языка L(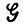) подвергаются воздействию механизма деформации , на рисунке этому соответствует второй оператор изображения, изменяющий под изображение. Результат предъявляется учителю и запоминается в кратковременной памяти Ω вместе с указанием, полученным от учителя, и недеформированным предложением. Допустим, что учитель отвечает только "да" или "нет" в соответствии с грамматической правильностью конкретного предложения. Мы будем обозначать функцию грамматической правильности через gr(⋅); она разумеется, неизвестна Ω априори. Значениями этой функции служат "ДА" и "НЕТ". Алгоритм абдукции обрабатывает эти три входа и передает результат в форме, которую еще следует определить, в долговременную память, после чего кратковременная память очищается. 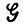По мере того как будет обрабатываться все большее число предложений, можно ожидать, что алгоритм сойдется к не которой предельной грамматике, эквивалентной в слабом смысле грамматике , причем параметры работы алгоритма будут характеризовать распределение вероятностей на L().

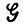В данной главе мы будем изучать абдукцию языка L(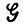) при полном отсутствии семантических входных сигналов, и, следовательно, связь env (Ω) с памятью, изображенная на рис. 7.2.1 пунктиром, отсутствует. Случай наличия семантического входа, поступающего из алгебры изображений env(Ω), представляет собой перспективную исследовательскую проблему, которая здесь, однако, изучаться не будет.

На рисунке представлены два оператора изображения: преобразователь, на выходе которого воспроизводятся предложения языка L(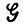), и - механизм деформации, кратко рассмотренный в предыдущем разделе и воспроизводящий на выходе цепочки символов того же словаря терминалов, что используется и во входных сообщениях. Определение алгоритма абдукции должно подробно задавать последний, и теперь мы перейдем к этому вопросу.

Во-первых, следует решить, какой тип грамматики должен здесь использоваться. Простым, но не тривиальным типом является автоматная грамматика, и именно ее мы будем использовать в качестве дальнейшие подробности, а также некоторые исторические сведения можно найти в примечаниях.

Здесь мы пользуемся теми же допущениями и обозначениями, что и в т. 1, разд. 2.4, 2.10 и 3.2. Словарь терминалов V_T содержит n_T слов, обозначаемых в общем случае буквами x, y, ... или этими же буквами, снабженными при необходимости нижними индексами. Синтаксические переменные, или не терминальные элементы, образуют некоторое множество V_N, включающее n_N элементов, которые обозначаются буквами i, j, ... или этими же буквами, снабженными при необходимости нижними индексами. Правила подстановки имеют вид

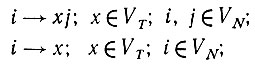(7.2.1)

последний тип правил приводит к окончанию вывода. Число правил подстановки обозначается через n_r. Соответствующие вероятности, образующие некоторую матрицу Р(x) и вектор r(x), обозначаются как p_ij(x) и r_i(x) соответственно. Кроме того,

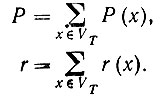(7.2.2)

При наших стандартных допущениях проблема состоятельности модели с синтаксически управляемой вероятностью автоматически решается положительно (см. теорема 2.10.7, гл. 2, т. 1, с. 76). Следовательно, на 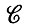() существует хорошо определенная вероятностная мера. Напомним, что в данном случае регулярные конфигурации характеризуются типом соединения ЛИНЕЙНЫЙ и показатели связей принимают значения из V_N. Естественно, внутренние связи должны удовлетворять отношению связи ρ = РАВЕНСТВО. Соответствующие изображения представляют собой "предложения" с одной входной и одной выходной связями.

Образующая представляет собой правило подстановки типа (7.2.1), так что ее можно рассматривать как некоторый элемент из V_T, т. е. слово, вместе с входными и выходными связями (I, I) или (i, F), где F представляет заключительное состояние. Начальное состояние будет выбираться как I = 1.

Заманчиво рассматривать образующую просто как некоторое слово из V_Т. Это, однако, неправильно, поскольку вполне может оказаться, что одно и то же слово x появляется в двух различных правилах i → xj и i' → xj'. Следовательно, отображение V_T → G - может быть многозначным, что, как мы убедимся ниже, имеет важные последствия.

Пусть x и y фиксированы в V_T выберем две произвольные цепочки u, υ∈V^*_T. Если всегда верно, что связанные конкатенацией цепочки uxυ и uyυ одновременно являются или не являются выводимыми в данной грамматике, то мы говорим, что x ≡ y, т. е. они эквивалентны (или конгруэнтны). Другими словами,

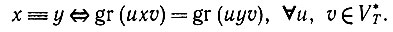(7.2.3)

Это позволяет разбить VT на классы эквивалентности. Отметим, что эквивалентность (7.2.3) требует, чтобы правая часть была справедлива при любых и и о. Следовательно, потребуется выполнить бесконечное число проверок, поскольку Vj бесконечен. Недостаточно провести проверку для одного (и, v) или некоторого конечного числа случаев. Тем не менее возникает ощущение, что если это соотношение справедливо для многих комбинаций (и, и), то, вероятно, х и у эквивалентны в некотором смысле, который точно еще не определен.

Нам понадобится следующее простое утверждение.

Лемма 7.2.1. Для того чтобы выполнялось x ≡ y, необходимо и достаточно, чтобы для любой образующей вида i → xj существовала образующая вида i → yj и наоборот.

Доказательство. Рассмотрим два слова x и y и цепочки uxυ и uyυ. Если для всякой образующей i → xj существует образующая i → yj, то очевидно, что gr (uxυ) = gr (uyυ), и поскольку это справедливо для любых u, υ∈V^*_T, то отсюда следует, что x ≡ y.

Выберем, с другой стороны, x и y так, чтобы выполнялось x ≡ y. Если uxy выводима в данной грамматике и и переводит начальное состояние в i-состояние, x переводит i-e состояние в j-е и υ переводит j-е в F, то для того, чтобы uyv также была выводима в данной грамматике, необходимо соответствие внутренних связей. Следовательно, должно существовать некоторое правило вида i → yj и, таким образом, доказательство закончено.

Чтобы выделить свойство эквивалентности, выбираем в качестве преобразований подобия множество всех тех подстановок образующих, которые не затрагивают эквивалентность, так что если gr = i → xj, то sg = i → x'j, причем x ≡ некоторый x'. Это определяет классы образующих G^α, инвариантные относительно S.

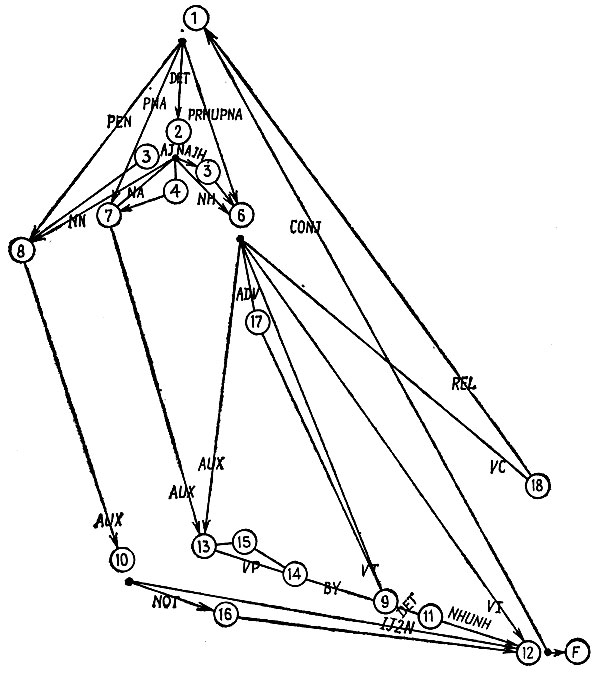
Рис. 7.2.2

Естественно, S не известны изначально и должны быть установлены посредством обучения в процессе абдукции. Мы начнем с некоторого множества S преобразований изображений, причем 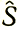необязательно должны образовывать группу. В качестве первой задачи, которой будут посвящены разд. 7.3 и 7.4, мы выберем определение (неизвестных) классов слов.

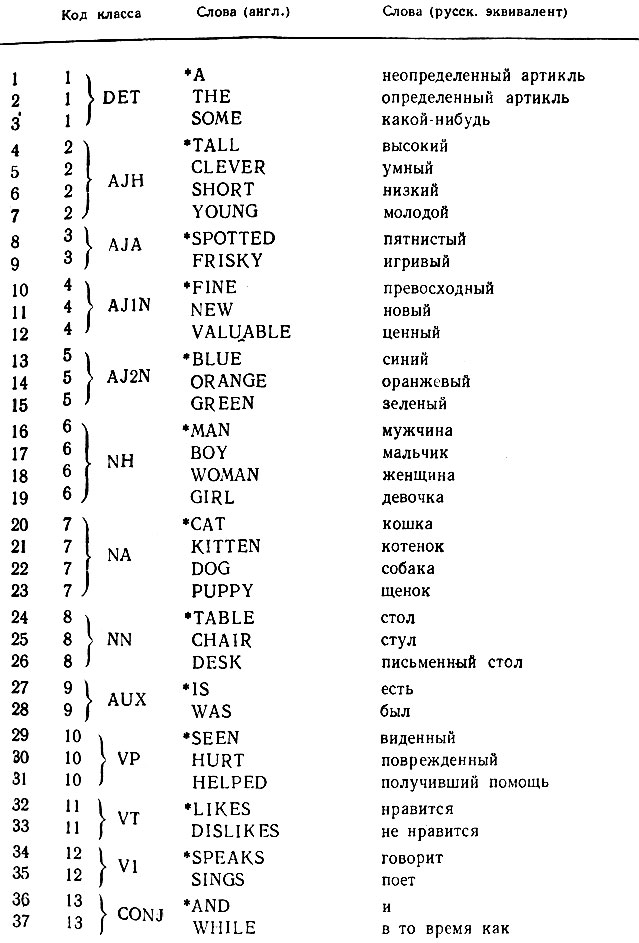
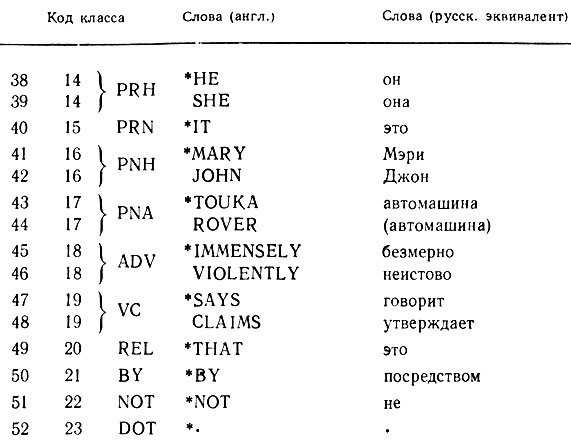
Таблица 7.2.1

Чтобы наше изложение было как можно более конкретным, мы воспользуемся некоторой "тестовой грамматикой". Конечно, можно было бы выбрать грамматику со словарем, состоящим из абстрактных символов, поскольку здесь мы не имеем дела с обработкой естественного языка. Однако по дидактическим соображениям мы выбрали грамматику, порождающую цепочки "английского" типа, с тем, чтобы результат было легче читать. Поскольку семантическая основа отсутствует, оказалось необходимым "подкрутить" грамматику так, чтобы избежать совершенно бессмысленных предложений.

Для данной грамматики n_T = 52, в том числе пунктуационный знак "⋅"; перечень слов терминального словаря приведен в табл. 7.2.1. Эти 52 "слова" сгруппированы в 23 класса слов, обозначенных, например, DET для определяющих слов, NH для слов, обозначающих людей, и т. д.

Тестовая грамматика 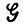имеет 19 состояний, включая заключительное состояние F = 19 (см. рис. 7.2.2.) Это соответствует образующим, перечисленным в табл. 7.2.2, где, например, 1 → PNA, 7 на самом деле представляет два правила подстановки, так как класс слов PNA содержит два слова. В общем мы располагаем 87 правилами.

Таблица 7.2.2

Программа порождает предложения языка L($) так, как это описано в разд. 3.2 т. 1. Реализация, естественно, зависит от вероятностей, сопоставленных образующим. Многие предложения вполне разумны, например такие, как "НЕ IS HELPED BY A BOY" (Ему помогает мальчик), "JOHN SPEAKS", (Джон говорит), "THE DESK IS NOT BLUE", (Стол -не синий). Некоторые предложения имеют несколько сомнительный характер, скажем такие, как "JOHN CLAIMS THAT JOHN SINGS" (Джон утверждает, что Джон поет) или "SOME VALUABLE TABLE IS NOT GREEN" (Какой-нибудь ценный стол -не зеленый). Реже появляются совсем странные предложения, например "НЕ CLAIMS THAT THE MAN CLAIMS THAT A WOMAN IS HELPED BY THE DOG" (Он утверждает, что мужчина утверждает, что женщине помогает собака) или "SHE VIOLENTLY LIKES THE BOY WHILE HE SPEAKS" (Ей неистово нравится мальчик в то время, как он говорит). Можно также отметить, что некоторые превосходные на вид английские предложения, порожденные' на основе заданного словаря терминалов, не допускаются , как, например, "ROVER LIKES THE GIRL" (Роверу нравится девочка). В целом наша грамматика достаточно сложна.

Рассмотрим теперь четыре образующие вида 11 → NH, 12. Слова в классе NH явно взаимно эквивалентны. Аналогичным образом четыре образующие типа 11 → NA, 12 используют слова класса NA, которые эквивалентны друг другу. Все эти восемь образующих переходят из состояния 11 в состояние 12, и может возникнуть искушение считать элементы класса NA эквивалентными элементам класса NH. На самом деле это, однако, не так, поскольку лемма 7.2.1 указывает, что для этого необходимо наличие, например, для образующих 2 → NH, 6 образующих вида 2 → NA, 6. Последние в % отсутствуют, и, следовательно, эквивалентность классов NA и NH не имеет места; последнее приводит к существенным затруднениям, которые будут изучаться в следующем разделе.