7.3. Разбиение слов на классы

Важнейший элемент алгоритма абдукции -это процедура поиска разбиения VT на классы эквивалентных слов. Если это удается сделать, то "комбинаторная сложность" задачи существенно понижается, так как в результате возникает возможность работать на уровне претерминалов вместо терминалов. Число слов в тестовой грамматике уменьшается при этом с 52 до 23. Вероятно, что при работе с естественным языком подобное сокращение окажется даже более существенным.

Но это не единственная причина того, почему этому вопросу уделяется столько внимания. Ниже мы убедимся, что именно в этой задаче разбиения и заключается основная математическая сложность: если она будет решена, то аналогичные рассуждения позволят справиться с задачей полной абдукции для автоматных грамматик. Следовательно, необходимо подробно изучить эту подзадачу.

Давайте установим, в чем именно состоит препятствие, не позволяющее использовать один из стандартных алгоритмов. Рассмотрим два слова x, y∈V^T и попробуем выяснить, эквивалентны они или нет. Допустим далее, что определена некоторая процедура проверки, которая будет применяться к некоторому заданному предложению I, порожденному в соответствии с моделью синтаксически управляемой вероятности.

Как было показано в предыдущем разделе, предложение I будет деформировано посредством и перейдет в I^D в результате замены одного или нескольких вхождений x в I на y. Если х не входит в I, никакие изменения не производятся. Нам придется точно описать, как происходит это замещение, когда мы подвергнем математическому анализу , но сейчас достаточно указать, что алгоритм не может быть абсолютно правильным и поэтому требуется ввести вероятности ошибок

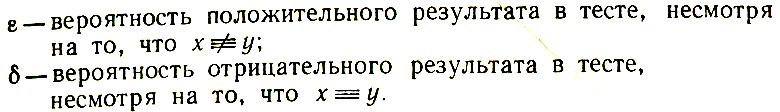(7.3.1)

Очевидно, что ε > 0 для некоторой 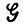, поскольку с положительной вероятностью может оказаться, что x ≠ y, но x допускает замену на y в некоторых предложениях, что не приводит к нарушению их грамматической правильности (см. последний раздел). Вторая вероятность 6 будет равна нулю, поскольку при x ≡ y любая подстановка x → y будет оставлять соответствующее предложение грамматически правильным. Если, однако, учитель "неидеальный", или, что то же самое, обучающийся функционирует в неидеальной лингвистической среде, то в этом случае также следует допустить, что δ > 0.

Для вычисления ε мы должны точно определить алгоритм тестирования; будет приведен один пример такого вычисления. При вариациях алгоритма тестирования соответствующее соотношение не будет выполняться точно, хотя оно может указать порядок ε. Допустим, что обнаружено первое вхождение x в I (если оно вообще имеет место) и проведена замена x на y. Чтобы определить ε_xy для фиксированных x и у, можно рассуждать так: Вероятность порождения какого-нибудь предложения, имеющего в первой позиции x и длину L, равна

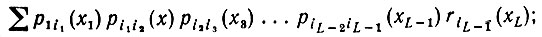(7.3.2)

где суммирование проводится по x₂, x₃, ..., x_L∈V_Т и по i, а сумма интерпретируется как r₁(x) при L = 1. Аналогично для получения некоторой цепочки, в которой первое вхождение x приходится на вторую позицию, соответствующая вероятность равна

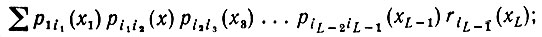(7.3.3)

суммирование проводится по x₁∈V^T - x, x₃, .., x_L∈V_T и по i. Можно выписать подобные выражения для любой позиции вплоть до L.

Определим

<(7.3.4) br>

Чтобы деформированное изображение I^D∈, необходимо при первом вхождении x в k-й позиции выполнение для некоторой последовательности j следующего соотношения:

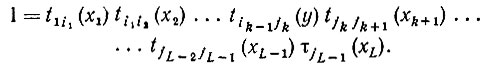
Событие, заключающееся в том, что I содержит x и I^D∈, будет тогда иметь вероятность p_xy, которую можно определить с помощью выражений (7.3.2) и (7.3.3), включив правую часть (7.3.5) в качестве множителя в члены этих выражений, суммируя, как было сказано, и, кроме того, по L = 1,2,3,... . Выполнив эти операции, мы получим следующее:

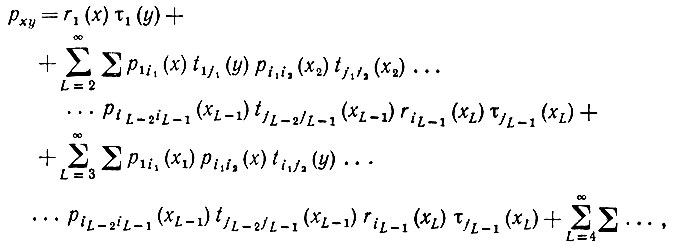(7.3.6)

где вторые знаки суммирования во всех членах обозначают суммирование по i и j и по x, но лишь при x₁ ≠ x во второй сумме, x₁ к x₂ ≠ x третьей сумме и т.д. Это выражение можно записать в более удобной форме, если ввести массивы:

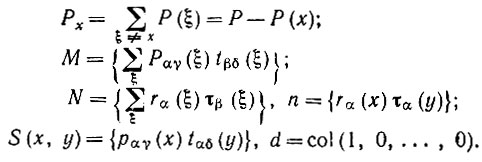(7.3.7)

Тогда выражение (7.3.6) можно записать как

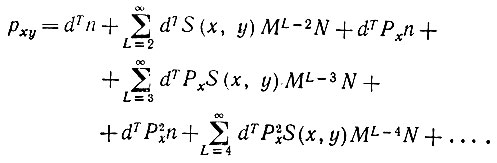(7.3.8)

Это дает нам

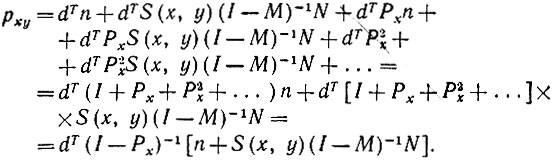(7.3.9)

Отметим, что S(x, y) и M - линейные операторы, представленные трехмерным и четырехмерным массивами соответственно, а второй единичный оператор I обозначает тождество, определенное с помощью четырех индексов: I = {δ_αβ, δ_γβ}.

С другой стороны, вероятность того, что некоторое предложение, принадлежащее модели синтаксически управляемой вероятности, не будет ни разу включать слово x, равна

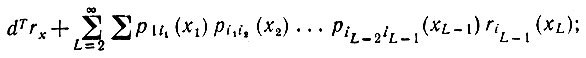(7.3.10)

суммирование проводится по x₁, x₂,..., x_L ≠ x если воспользоваться (7.3.7), то последнее выражение приобретает следующий вид:

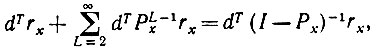(7.3.11)

где r_x = r - r(x).

Рассмотрим ε_xy - условную вероятность того, что x ≠ y не обнаружено, если x входит в предложение и заменяется на y:

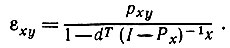(7.3.12)

Из-за наличия множителя (1 - М)^-1 в выражении (7.3.9) создается впечатление, что его трудно непосредственно вычислить. Можно предложить прямую и полезную интерпретацию матрицы Q = (1 - M)^-1N. Обратимся к рис. 7.3.1, на котором представлено порождение двух рассматриваемых цепочек nxυ и nyυ. Обратившись к (7.3.6), нетрудно убедиться в том, что элемент q_γδ матрицы Q представляет собой вероятность порождения некоторой под цепочки, началом которой служит состояние у, а концом - состояние F, причем та же лексическая цепочка обеспечивает также переход из состояния δ в F. Матрица Q не должна быть обязательно симметрической.

Элементы q должны подчиняться рекуррентному соотношению

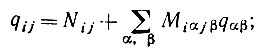(7.3.13)

это можно получить также исходя из алгебраического определения матрицы Q. Важнее, однако, осознать что элемент q_ij должен быть равен нулю, если не существует слова ξ источником которого являются как i, так и j. Другими словами,

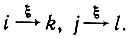
Это означает, что Q будет исключительно слабо заполненной матрицей, в которую можно априори занести множество нулей при помощи простого просмотра диаграммы. Более того, для элемента главной диагонали g_ii это значение представляет собой просто вероятность порождения некоторой цепочки, обеспечивающей переход из состояния i в состояние F. В соответствии с принятыми нами допущениями эта вероятность автоматически равна единице.

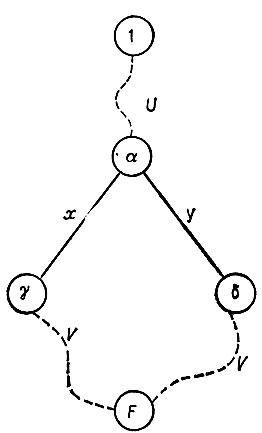
Рис. 7.3.1

Введем отношение Е, связывающее состояния, причем iEj, если существуют ξ∈V^T k и l, такие, что

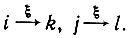
Пусть Е^* - транзитивное замыкание Е, и, следовательно, Е^* - это отношение эквивалентности. Тогда Е^* разбивает множество состояний на классы, а матрица Ω оказывается разбитой на блоки, причем индексы строк и столбцов блоков будут соответствовать классам, индуцированным Е^*. Таким образом, вычислительные проблемы, возникающие в связи с (7.3.12), становятся преодолимыми.

Объединив (7.3.11) с (7.3.9), мы получаем вероятность е_xy того, что деформация d(x → y) не обнаруживает x ≠ y:

(7.3.14)

При повторном применении этой деформации к последовательным предложениям можно, следовательно, считать, что эта процедура повторится порядка 1/(1 - е_xy) раз. При больших значениях е_xy потребуется существенный объем тестирования, однако мы попытаемся понизить его, улучшив вид алгоритмов разбиения.

Эмпирически в процессе моделирования описываемых было установлено, что выбор x из I можно усовершенствовать. "Механические" критерии, такие, как выбор первого встречающегося x, где x в свою очередь выбирается из V^T случайно, исключительно неэффективны. То же относится и к случайному выбору вхождений (возможных) x в I.

Вместо этого следует выбирать хну так, чтобы проверке подвергались лишь "критические" случаи, когда существуют реальные основания предполагать, что x ≠ yΘ, и не затрачивались впустую усилия на частые проверки x и y, если уже имеется достаточная уверенность в том, что х==у. Эта идея была реализована так:

Шаг 1. Работа алгоритма начинается с создания единственного класса, включающего все V^T, и выбора одного слова в качестве прототипа класса.

Шаг 2. Алгоритм СЛУШАТЬ порождает какое-либо предложение языка L() в соответствии с моделью синтаксически управляемой вероятности (неизвестной).

Шаг 3. Алгоритм ВНИМАНИЕ (см. ниже) выбирает x∈I вызывается текущий прототип y. Производится переход к шагу 4, если x - прототип, x = y, в противном случае переход к шагу 5.

Шаг 4. Выбирается другое слово z из класса, содержащего этот прототип, с вероятностями, убывающими с расстоянием. Проверяется gr(I^D), I^D = (y → z) I, и над z осуществляются те же операции, что осуществляются над x на шагах 6 - 8. Переход к шагу 2.

Шаг 5. Алгоритм ГОВОРИТЬ воспроизводит деформированную цепочку I = d(x → y)I, где y равен прототипу того класса, к которому в данный момент принадлежит х. Определяется грамматическая правильность I^d. Переход к шагу 7, если gr(/^)=^0)Kb.

Шаг 6. Если gr(I^D) = ИСТИНА, то алгоритм УСИЛИТЬ увеличивает правдоподобие x = y за счет того, что x перемещается ближе к y в данном классе, если это возможно. Другими словами, x и соседний по направлению к у элемент меняются местами до тех пор, пока соседним элементом не окажется y. Переход к шагу 2 (или останов).

Шаг 7. x перемещается к концу соседнего класса, если таковой существует; в противном случае переход к шагу 8.

Шаг 8. Создается новый класс, в котором x является единственным элементом и прототипом.

Перечень текущих классов можно представить так, как это сделано на рис. 7.3.2, где указаны типичные перемещения слов, x₁₁, x₂₁,...,x_l1 - прототипы.

Алгоритм ВНИМАНИЕ предназначен для того, чтобы избежать неэффективного тестирования и сконцентрировать процесс абдукции на гипотезах, по которым в данный момент нет ясности. При этом рассматривается множество слов текущего изображения. Текущие списки удобно рассматривать как списки, упорядоченные слева, причем прототип занимает в них крайнее левое положение. Для каждого слова измеряется его расстояние от крайнего слева элемента -прототипа. Алгоритм ВНИМАНИЕ случайно выбирает одно слово, причем не с равномерным распределением, а с вероятностями, монотонно возрастающими в соответствии с расстоянием от прототипа в текущем классе слова.

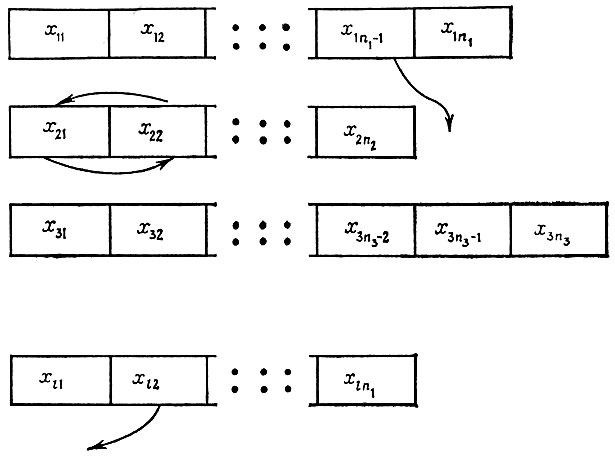
Рис. 7.3.2

Алгоритм УСИЛИТЬ корректирует гипотезу о том, что x = y, перемещая x влево, в положение, где вероятность эквивалентности прототипу больше.

Теорема 7.3.1. Алгоритм обеспечивает разбиения, сходящиеся с вероятностью единица к истинному разбиению за конечное число шагов.

Доказательство. Рассмотрим последовательность предложений I⁽¹⁾, I⁽²⁾, ..., I^(t), воспроизведенных алгоритмом СЛУШАТЬ, и обозначим через с_t число классов, сформированных после прослушивания t предложений. Поскольку величина c_t не убывает по t и ограничена величиной n_T она сходится к некоторой предельной случайной величине с_∞. Если с_∞ меньше истинного числа классов, то существует по крайней мере одно слово, скажем x, неэквивалентное ни одному из с_∞ прототипов. Пусть Е - вероятность того, что при заданных см прототипах будет порождено предложение, содержащее x и такое, что выбор и тестирование x по всем прототипам дают отрицательные результаты. Тогда Р(Е) положительна, хотя, быть может, и очень мала. При наличии события Е шаг 8 алгоритма вводит новый класс. Используя обращение леммы Бореля - Кантелли (см., например, Феллер (1967), т. 1, с. 205), мы обнаруживаем, что это имеет место с вероятностью единица для бесконечной последовательности предложений, порожденных так, что с_∞ почти наверное равна истинному числу классов. Благодаря способу выбора прототипов они все взаимно неэквивалентны. Следовательно, с вероятностью единица они представляют истинные классы эквивалентности, хотя их "маркировка" может отличаться от использовавшейся первоначально.

Перемещения, обусловленные алгоритмом (см. рис. 7.3.2.), происходят частично в пределах "своих" классов, а частично между классами. Первый тип перемещений непосредственно на разбиение не влияет и характеризует лишь изменения наших представлений. Второй тип перемещает слово вниз, в другой класс или в некоторый новый класс. Это означает, что, как только значение n_∞ достигнуто, алгоритм лишь удаляет слова из тех классов, к которым они не принадлежат. Слово х почти наверное не будет оставаться в неправильном классе на протяжении более чем конечного числа итераций. Следовательно, разбиения сходятся к истинному разбиению после некоторого конечного числа шагов.

Наша теорема гарантирует состоятельность этого процессора образов, но ничего не говорит о скорости сходимости. Чтобы разобраться с этим вопросом, несколько совершенно различных вариантов алгоритма были реализованы и опробованы на вычислительной машине.

Для случая тестовой грамматики (разд. 7.2) слова были быстро разбиты на классы эквивалентности еще на ранней стадии выполнения алгоритма. Затем скорость обучения существенно уменьшается. В типичном прогоне после прослушивания и обработки 200 предложений была определена большая часть из 23 классов эквивалентности и лишь два слова из 52 были классифицированы неверно.

Соответствующие графики приведены на рис. 7.3.3, где представлено число правильно классифицированных слов в зависимости от числа предложений, и на рис. 7.3.4, где показано количество выделенных классов слов.

В каком-то смысле этот алгоритм абдукции удовлетворяет требованиям разд. 7.2. "Единственный" он или нет - об этом можно судить по-разному, но этот алгоритм по крайней мере более естествен, чем некоторые альтернативные варианты. Он явно обладает быстродействием, хотя мы ничего не утверждаем относительно его оптимальности, он нечувствителен к ошибке ε, которая играет фундаментальную роль в выводе на основании правдоподобия.

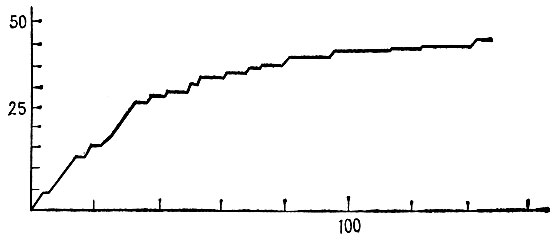
Рис. 7.3.3

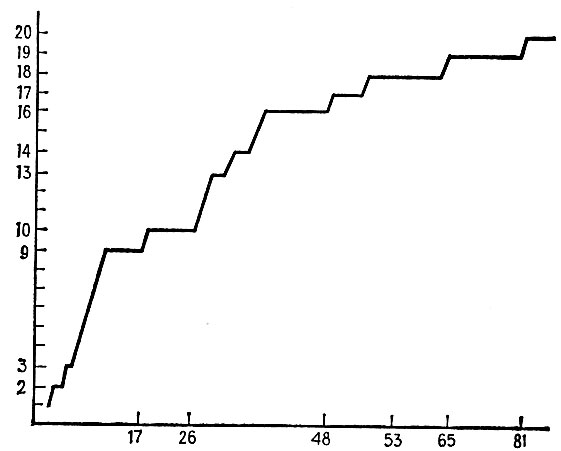
Рис. 7.3.4

Если, однако, структура образов изменяется, то этот алгоритм выглядит менее привлекательно. Точнее, если ответ, сообщаемый обучающемуся, относительно значения gr(I^) верен не всегда, так что обучающемуся может быть сказано, что хотя I^D∈, то δ > 0 (СМ. предыдущий раздел).

Тщательно анализируя алгоритм, можно установить, что шаг 8 может быть осуществлен, когда x действительно эквивалентен прототипу одного из текущих классов эквивалентности. Следовательно, существует положительная вероятность того, что будет введено слишком много текущих классов эквивалентности. Поскольку в алгоритме отсутствует шаг, предусматривающий объединение классов, эта ошибка не будет устранена вообще.

Следовательно, алгоритм не обладает устойчивостью относительно небольших (δ-малое) изменений в структуре образов лингвистической среды обучающегося. Возникает проблема, как компенсировать эту ошибку.

Одна из возможностей заключается в том, чтобы ввести в алгоритм объединяющий шаг, который будет исполняться лишь время от времени. Хотя это и можно сделать, мы не будем предпринимать такой попытки, поскольку это нарушило бы элегантную простоту алгоритма. Вместо этого мы рассмотрим алгоритм другого типа.