7.5. Обнаружение синтаксических переменных

Восстановление разбиения слов на классы представляет собой лишь часть задачи абдукции грамматики в целом. Теперь мы приведем два метода, позволяющие придать алгоритму завершенность. Первый из них обладает простотой и непосредственностью, но является неэффективным в смысле использования памяти и, что в нашем случае хуже, несколько неестественным. Второй алгоритм сложнее, но он более естественный и, возможно, много более эффективный.

Обращаясь к диаграмме состояний грамматики, будем иметь в виду хорошо известный факт, что состояния (синтаксические переменные) в некоторой минимальной машине представляют собой классы эквивалентности цепочек (а не отдельных слов). Так, например, на рис. 7.2.2 состояние 3 содержит все цепочки DET, AJH, а также некоторые другие, состояние 7 содержит все цепочки, которые могут быть записаны как PNA или DET, AJA, NA. Множество всех конечных цепочек, разумеется, бесконечно, но всегда можно достичь любое состояние посредством цепочек длины, не превышающей некоторое конечное число. Минимальное из этих чисел D называется глубиной грамматики.

Рассмотрим множество V^D_T, которое будет разбито на классы эквивалентности, в том числе классы для заключительного состояния и "не грамматического" состояния, т. е. состояния, не позволяющего перевести цепочку в предложение, выводимое в данной грамматике.

Для того чтобы восстановить состояния, теперь можно действовать так же, как и в разд. 7.3, за тем исключением, что здесь мы заменяем одни другими. В данном случае вместо одних исходных цепочек подставляются другие исходные цепочки, причем используются при этом лишь цепочки самое большее длины D. Напомним также, что употребляемые здесь символы являются на самом деле претерминальными элементами исходной грамматики, поскольку работа ведется с классами слов, которые уже восстановлены. Но тогда эта процедура логически эквивалентна процедуре, с которой мы имели дело в разд 7.3, и утверждение, высказанное тогда относительно сходимости, можно непосредственно распространить на обнаружение состояний: состояния будут в пределе установлены состоятельно.

После того как состояния идентифицированы, оказывается возможным также определить связывающие их правила подстановки. Например, в процессе обучения будет установлено, что состояние 6 содержит цепочки типа DET, AJH и NH, так что существуют ветви, ведущие из состояния 3 ≡ DET, AJH и т. д. в состояние 6 с лексическими элементами NH.

Именно этот алгоритм был первым из опробованных в отчете Гренандера (19746); он был успешно применен к нескольким небольшим тестовым грамматикам. Для больших грамматик он не подходит, поскольку потребность в памяти быстро возрастет. Число исходных цепочек, равное

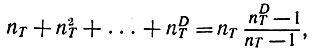(7.5.1)

экспоненциально растет с увеличением глубины грамматики, и при существенных значениях последней уже невозможно обрабатывать цепочки. Кроме того, неестественно вводить все исходные цепочки и осуществлять полный перебор в V^D_T.

Рассмотрим в качестве альтернативы следующий алгоритм, включающий несколько больше элементов из алгоритма, описанного в разд. 7.3. Воспользуемся расщеплением состояний, учитывая ошибку ε, возникающую здесь аналогично случаю разбиения слов на классы эквивалентности.

Мы начинаем с создания единственного класса, обозначаемого как и содержащего лишь пустую цепочку НУЛЕВАЯ. В каждом классе будет выделен один элемент, называемый прототипом, так что в классе прототипом окажется НУЛЕВАЯ. Отметим, что ниже состояние 1 не должно обязательно соответствовать классу .

Обучающийся слушает предъявляемые ему грамматически правильные предложения и пытается обнаружить состояния, достижимые за d шагов из состояния 1 как начального, при d = l, 2, 3,... . Допустим на время, что d = 1 и предложение имеет вид x₁x₂x₃.. .x_l. Проверяем эквивалентность x₁ прототипу НУЛЕВАЯ. Если ответ положительный, то зачисляем цепочку НУЛЕВАЯ, x₁ в класс , в противном случае проверяем ее на эквивалентность прототипу класса , если такой класс уже создан и т. д. Мы также время от времени выбираем некоторый прототип и заменяем его другим словом, после чего проводим проверку грамматической правильности и повторяется та же, что и выше, процедура. Если оказывается, что существующие в данный момент r прототипов неэквивалентны x₁, то создаем некоторый новый класс, скажем 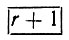и x₁ назначается его прототипом.

Повторяем эту процедуру много раз, допустим N1 = vlN. Рассмотрим затем начальные цепочки при d = 2, x₁x₂, которые можно представить как некоторый , соединенный с помощью конкатенации с x₂. Далее посредством той же процедуры формируем новые классы, повторяя ее, скажем, N₂ = υ₂N раз. Переходим к цепочкам длины 3 и т. д.

В качестве иллюстрации изложенного рассмотрим простую схему, изображенную на рис. 7.5.1. Допустим, что сформированы предложения, помещенные в табл. 7.5.1. Отметим, что ε > О, поскольку а и b неэквивалентны, но могут показаться эквивалентными в 4 → F.

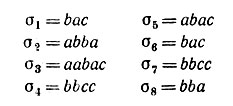
Таблица 7.5.1

Для начала мы имеем лишь один класс, содержащий НУЛЕВУЮ. Прослушивая σ₁ мы проверяем эквивалентность x₁ = НУЛЕВАЯ. Поскольку НУЛЕВАЯ x₂x₃ = ac∈L, то мы создаем класс , включающий прототип b. В σ² проверяется эквивалентность x₁ = а НУЛЕВАЯ и, поскольку bba∈L, а зачисляется в класс . Для σ₃ получаем тот же результат. Для σ₄ мы зачисляем x₂ = b в класс , который уже сформирован. Повторяя эту операцию N₁ раз, мы не получим новых классов.

Положим далее d = 2 и прослушаем, скажем, σ₅. Поскольку x₁x₂ = ab = b, то это некоторый прототип и никакой корректировки не требуется. Для σ₆ = bac при x₁x₂ = ba = a сопоставление этого выражения с НУЛЕВОЙ дает отрицательный результат, затем проводится сопоставление с b, которое также дает отрицательный результат, и, следовательно, необходимо учредить некоторый новый класс с прототипом a. Для σ₇ мы также получаем некоторый новый класс с прототипом b.

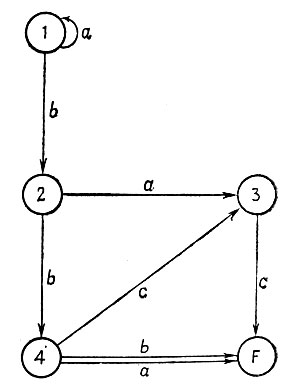
Рис. 7.5.1

После этого скорректированные таблицы будут иметь вид

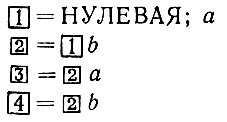(7.5.2)

и мы продолжаем действовать, как было описано, заменяя иногда, как отмечалось, слова формальными прототипами. Окончательный результат может выглядеть так:

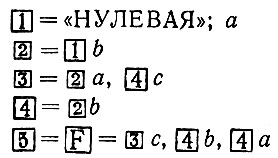(7.5.3)

Отметим, однако, что нумерация классов может отличаться от нумерации i состояний на исходной схеме. Взгляните на ветви схемы -рис. 7.5.1.

При N → ∞ вероятность того, что в слабом смысле восстановленная грамматика эквивалентна истинной, стремится к единице; доказательство этого факта аналогично доказательству теоремы 7.3.1. Однако этот алгоритм не был реализован и проверен на ЭВМ, так что скорость его сходимости абсолютно неизвестна.

Одно из непривлекательных свойств этого алгоритма заключается в том, что он последовательный. Более сложный вариант этого алгоритма, имеющий последовательный характер, предложен Шриром, и на его основе очень тщательно составлена программа (см. Шрир (1977)). Использование ее в качестве проверочной программы разд. 7.2 позволило восстановить большинство синтаксических переменных, за исключением нескольких, после того как были предъявлены 50 предложений и выполнено разбиение слов на классы. Это довольно высокая скорость, а потребность в памяти невелика.

Важнее, однако, чем характеристики, относящиеся к затратам времени и памяти, является основной принцип, на который опирается алгоритм абдукции такого типа. Регулярная структура, на которую он ориентирован, основана на использовании правил подстановки в качестве образующих. Алгоритмы предназначены для непосредственной идентификации образующих, и именно эта тесная связь со структурой образов придает алгоритму столь естественный облик.