Приложение 2. I. О принципиальной осуществимости конечного автомата, безошибочно опознающего не пересекающиеся образы

Метод эталонов для ε-непересекающихся образов в принципе может обеспечить безошибочное опознание учебной выборки любого объема. Для доказательства принципиальной осуществимости конечного автомата, обладающего нулевой ошибкой, достаточно показать, что даже на гипотетической бесконечной учебной выборке число блоков опознающей машины, служащих для создания признаков и принятия решения, конечно.

Покажем сначала, что система признаков является конечной.

При детермипироваино-статистическом методе признаки конструируются как линейные функционалы от исходного описания образов. Конечная система признаков аппроксимирует исходное описание образов и может быть связана с некоторым конечномерным базисом, выбранным из пространства исходного описания так. чтобы не ухудшались условия разделимости образов.

Не ограничивая общности, будем считать, что описания объектов опознания являются функциями некоторой переменной. (Если исходное описание конечномерное, то система признаков заведомо конечна.) Во всех известных нам технических задачах опознания образы описываются семействами функций, компактными^* в гильбертовом пространстве L₂ сразу для всех функций семейства.

^* (Для того чтобы семейство функций

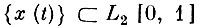
было компактно [2.5], необходимо и достаточно, чтобы функции семейства были равномерно ограничены по норме и равностепенно непрерывны в среднем, т. е.

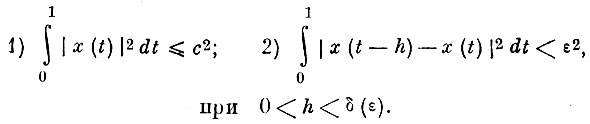
Условия (1) и (2) не являются очень жесткими для физических функций. Условие (1) всегда выполняется, так как энергия реального сигнала всегда конечна.

Условие (2) выполняется для тех функций, которые имеют конечное число разрывов 1-го рода, причем величины скачков равномерно ограничены, а на оставшемся множестве выполняется условие Липшица с общей постоянной К. )

Предложение 1. Если образы не пересекаются и описаниями объектов опознания каждого образа являются семейства функций, компактные в пространстве L₂, то существует конечная система признаков, для которой аппроксимированные описания образов также не пересекаются.

Доказательство этого положения дано в следующей теореме.

Теорема 1. Если расстояние между двумя компактными семействами функций

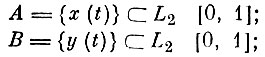
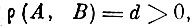
то существует такое конечномерное эвклидово пространство

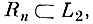
что расстояние между проекциями семейств функций А и В на это эвклидово пространство

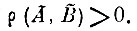
Доказательство. На каждом из компактных семейств функций А и В построим конечную ε-сеть, взяв ε = d/3. Обозначим множества, покрываемые ε-сетями, через А_ε и В_ε, а множества, покрываемые ячейками (сферами) ε-сетей, через

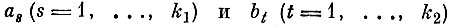
соответственно. Для каждой пары сфер

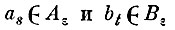
построим вектор z_st, соединяющий две ближайшие точки этих сфер. Заметим, что по построению

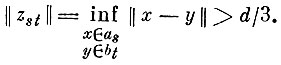
Линейная оболочка

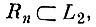
порождаемая системой векторов z_st, имеет конечную размерность

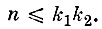
Спроектируем ортогонально множества А_ε и В_ε на подпространство R_n и покажем, что расстояние между проекциями Ã_ε и В̃_ε. множеств А_ε и В_ε на это подпространство

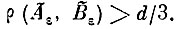
Для этого выберем в подпространстве R_n ортонормированный базис так, чтобы один из ортов, скажем,

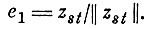
Расстояние между проекциями множеств А_ε и B_ε па построенное эвклидово пространство

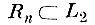
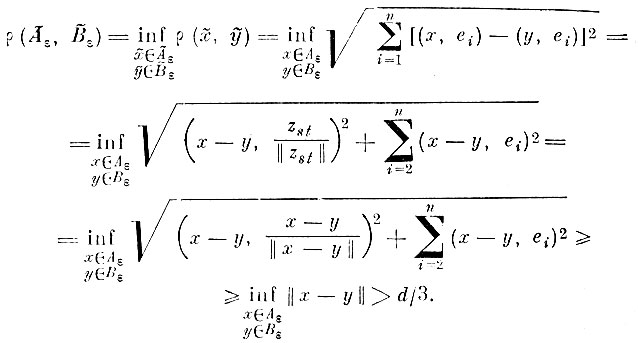
Отсюда расстояние между проекциями множеств А и B на подпространство R_n

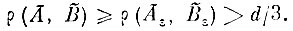
Теорема доказана.

Выбирая в пространстве B_n любой другой линейно-независимый базис

получим конечное разложение для каждой функции семейств А и В:

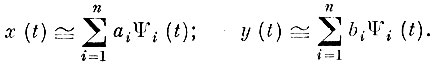
Из теоремы 1 следует, что если семейства функций А и В компактны в L₂[0, 1] и расстояние между ними d > 0, то существует конечное линейное разложение (единое для всех функций семейств), для которого расстояние между аппроксимированными семействами функций d₁ > 0.

Покажем теперь, что число эталонов, образующих решающее правило, также конечно.

Напомним, что каждый эталон, реализованный в блоке принятия решения, покрывает некоторое подмножество объектов данного образа и не "захватывает" при этом ни одного из объектов чужих образов.

Предложение 2. Если для образов выполняется условие ε-непересекаемости и описаниями объектов опознания каждого образа являются семейства функций, компактные в банаховом пространстве, то число эталонов каждого образа, выполненных в любой из метрик банахового пространства, конечно.

Доказательство этого положения изложено в теореме 2.

Теорема 2. Если в банаховом пространстве расстояние между компактным множеством A множеством В

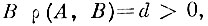
то существует конечное число сфер, покрывающих все элементы множества А и не покрывающих ни одного из элементов множества В.

Доказательство. Построим на множестве А конечную ε-сеть, взяв

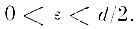
Построенная ε-сеть покрывает все элементы множества А и не покрывает ни одного из элементов множества В. Следовательно, число эталонов (ячеек ε-сети) для образа А, выполненных в любой из метрик бапахового пространства, является конечным.