Глава третья. Оценка меры не пересекаемости образов по конечной выборке

§ 3.1. Введение

В главе II указывалось, что одним из основных ограничений при использовании детерминироваино-статистического подхода является выполнение условия ε-непересекаемости образов.

По определению [3.1 ], образы называются ε-непересекаемыми, если при неограниченном возрастании объемов выборок всех образов минимальное взаимное расстояние между реализациями различных классов остается не менее некоторой конечной величины в, т. е.

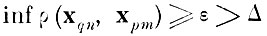(3.1.1)

где x_qn - n-я реализация g-го образа; q, р - номера образов; Δ - величина аппаратурной погрешности.

Очевидно, что величина в, характеризующая не пересекаемость образов, должна быть больше, чем аппаратурная погрешность Δ опознающего автомата.

Геометрически выполнение условия (3. 1. 1) означает существование в пространстве исходного описания некоторого, возможно достаточно сложного по конфигурации, "коридора" между образами, "ширина" которого, однако, не меньше ε.

Проверка выполнения условия ε-непересекаемости дает ответ на вопрос о том, разделимы ли принципиально образы в пространстве исходного описания, т. е. имеет ли смысл продолжать проектирование опознающего автомата или следует искать новое исходное описание.

Аналогичная проверка выполнения условия (3. 1. 1) в пространстве признаков позволяет выяснить, сохраняются ли условия существования безошибочных решающих правил в сокращенном описании, т. е. пригодно ли найденное пространство признаков для последующего принятия решения.

Определение меры не пересекаемости образов (3. 1. 1) является предельным соотношением для бесконечной выборки, в то время как объемы учебных выборок всегда конечны, поэтому получить оценку ε можно лишь в статистическом смысле, например, построением асимптотически несмещенной точечной оценки минимального расстояния между образами, а также нахождением для нее доверительного интервала.