§ 3.2. Обоснование процедуры получения оценки меры не пересекаемости образов по учебной выборке

Рассмотрим функцию распределения F (r) взаимных расстояний между реализациями различных образов. Из определения (3. 1. 1) следует, что величина ε является предельной точкой этой функции (т. е. F (ε)=0).

Вид F (r) считается неизвестным, так что оценка меры непересекаемости относится, вообще говоря, к непараметрическим задачам математической статистики. Однако, постулируя некоторые не очень стеснительные в практическом отношении ограничения, удается, используя методы статистики экстремальных значений [3. 2], свести задачу получения оценки минимального взаимного расстояния между образами к параметрической.

Обоснование этого метода заключается в том, что, согласно теории крайних членов, только три типа законов распределения могут выступать в качестве предельных для выборочных экстремумов^* если исходная функция распределения удовлетворяет некоторым условиям, которые для технических задач опознания, как правило, выполняются.

1^* (Экстремумами, или крайними членами выборки, называются члены вариационного ряда х₁, х₂, . . . , х_m, . . . , х_n, ранг которых m (или n-m+1) остается постоянным при увеличении объема выборки n, т. е. отношение m/n убывает. Соответствующие значения х_m называются m-ми экстремальными значениями [3.2]. В дальнейшем будут рассматриваться только собственно экстремальные значения, т. е. порядковые статистики ранга m = 1. )

В частности, если неизвестная функция распределения взаимных расстояний F (r) непрерывна, ограничена слева^*, а также подчиняется слева некоторому условию гладкости^**, то распределение независимых минимальных расстояний между образами (экстремумов) будет отвечать третьему типу распределения крайних членов выборки.

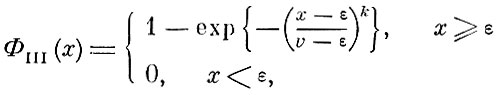(3.2.1)

где v, k, ε - параметры этого распределения.

^* (Функция распределения взаимных расстояний точно ограничена слева нулем, т. к. расстояния - неотрицательные величины и есть подозрение, что она ограничена слева некоторой величиной ε, которую и требуется оценить.)

^** (Допущение о выполнимости этого условия фактически означает, что к своей левой предельной точке ε функция распределения взаимных расстояний между образами F (r) подходит достаточно гладко, а именно, что в окрестности r = ε + h , h → 0 она может быть приближенно описана равенством

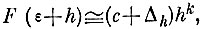
где с > 0, 0 < k < ∑, Δ_h → 0 при h → 0.)

В остальном F (r) может быть совершенно произвольна.

Следовательно, если но учебной выборке получить выборку независимых экстремальных взаимных расстояний между классами, то последняя подчиняется распределению (3. 2. 1). И таким образом, оценка меры не пересекаемости образов сводится к оцениванию по выборке экстремумов параметра ε в распределении (3. 2. 1) и построению для него доверительного интервала^*.

^* (Специфика статистики крайних [3.2] приводит к некоторым особенностям этой параметрической задачи, которые мы обсудим в приложении 3.1.)

Выборка независимых минимальных взаимных расстояний может быть получена по учебной выборке следующим способом.

Составляется первая выборка независимых (или слабо-зависимых) расстояний объема n и из нее выбирается наименьшее взаимное расстояние r⁽¹⁾₁ - порядковая статистика ранга один^*.

^* (Вообще говоря, распределение (3. 2. 1) справедливо лишь для п зависимых наблюдений. Однако, так как распределение экстремумов определяется лишь поведением исходной функции распределения F (r) на левом "хвосте", то минимальные расстояния, полученные по слабо-зависимой исходной выборке взаимных расстояний, будут практически оставаться независимыми. Независимость исходной выборки является менее важной для статистики экстремальных значений, чем это кажется с первого взгляда. Эти соображения подтверждаются, например, в практике предсказания паводков и усталостных напряжений [3. 2].)

Затем составляется другая независимая выборка взаимных расстояний и аналогично находится второй экстремум r⁽²⁾₁ и т. д.

Полученная выборка

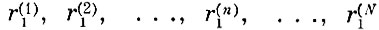
порядковых статистик ранга один и есть выборка минимальных (экстремальных) взаимных расстояний, которая подчиняется распределению (3. 2. 1).

Объем n исходных выборок взаимных расстояний должен быть, очевидно, настолько велик, чтобы получаемые по этим выборкам минимальные расстояния могли с заданной вероятностью считаться экстремумами.

Для оценки необходимой величины этого объема используют так называемый односторонний толерантный предел [3.2]:

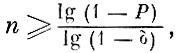(3.2.2)

где Р - вероятность того, что в будущей большой выборке не более δ-й части окажется меньше наименьшего взаимного расстояния в прошлой выборке объема n; δ - относительное число (доля) будущих взаимных расстояний, которые меньше наименьшего в выборке объема n.

Так, например, для получения одного экстремума "однопроцентного порядка" (δ=0,01) с вероятностью P=0,95 требуется выборка исходных взаимных расстояний объема

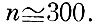
Необходимый объем выборки, как функция процентной доли 8 и вероятности Р, представлен на рис. 3.1.

С другой стороны, число таких экстремумов N (т. е. число частных выборок исходных взаимных расстояний) должно быть также достаточно велико, чтобы оценить с удовлетворительной точностью параметры распределения (3. 2. 1).

В самом деле, для оценки трех параметров в распределении (3. 2. 1), например методом моментов, приходится по выборке экстремумов вычислять три первых выборочных центральных момента. Для оценки третьего момента (асимметрии) число наблюдений порядка 100 не может считаться достаточно "большим" [3.3].

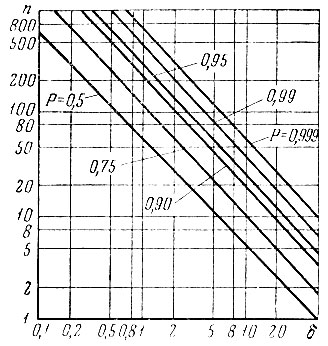
3.1. Зависимость необходимого объема выборки n от Р и δ

Таким образом, при оценке меры не пересекаемости требования к объемам учебных выборок для задачи попарного разделения образов могут оказаться чрезмерно жесткими.

В задачах опознания многих образов, когда можно дополнительно ввести физическое предположение о том, что каждому образу есть свой близкий другой образ (или близкая группа образов), количество реализаций на класс может быть значительно меньшим, если разумно организовать смесь взаимных расстояний между близкими группами образов^*.

^* (Известно [3.2], что такая процедура смешивания использовалась в задачах предсказания паводков. Для удлинения записей расходов воды объединяли записи для различных рек на основании некоторого критерия однородности.)

В этом случае процедура создания выборки минимальных взаимных расстояний заключается в следующем. Исходная слабозависимая (см. сноску на стр. 46) выборка взаимных расстояний близких классов разбивается случайным образом на N групп по n элементов в каждой (с учетом сделанных выше замечаний о величине n). В каждой группе перебором находится экстремум - порядковая статистика ранга один. Совокупность этих минимальных расстояний и образует смешанную выборку экстремумов.

По полученной выборке экстремумов следует теперь оценить параметры третьего распределения крайних членов (3. 2. 1). Методика оценки параметров изложена в приложении 3.1. Здесь приведем лишь окончательные формулы оценок меры не пересекаемости образов.

Точечная оценка метрической близости образов имеет вид:

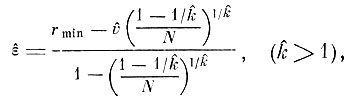(3.2.3)

где r_min - минимальное выборочное расстояние между образами; v̂ - оценка параметра v (так называемого характеристического значения распределения минимумов); k̂ - оценка параметра k, характеризующего асимметрию распределения (3. 2. 1); N - объем выборки экстремумов.

Условный доверительный интервал для в может быть записан в виде

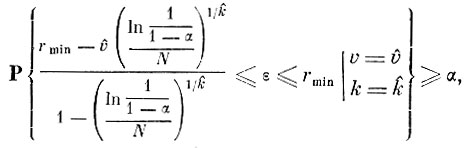(3.2.4)

где α - доверительная вероятность, а остальные параметры те же, что и в (3. 2. 3).