Приложение 3. I. Методика получения точечной и интервальной оценок величины ε

Пусть

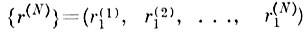
выборка экстремумов, т. е. выборка первых порядковых статистик в N исходных независимых выборках взаимных расстояний между образами. Эти минимальные расстояния при выполнении ограничений, изложенных в § 3.2, принадлежат распределению (3. 2. 1). Требуется оцепить параметры этого распределения по выборке экстремумов.

Обычно в практических задачах объем выборки экстремумов не слишком велик (N ≤ 100), поэтому метод моментов [3.5] не может дать удовлетворительной точности, так как выборочная асимметрия (приведенный третий центральный момент) имеет значительные погрешности для таких объемов выборки [3.3].

Поэтому поступают следующим образом: параметр v (так называемое характеристическое значение, т. е. такое, что Φ_III(с) = 1/е) оценивают независимо как порядковую статистику, ранг которой определяется из соотношения

Следовательно, оценка параметра v получается интерполяцией между m-м и (m+1)-м значениями минимальных расстояний r^(m)₁ и r^(m+1)₁ в вариационном ряду выборки экстремумов. Рекомендуется [3.2] линейная интерполяция между

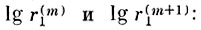
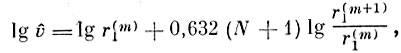(3.1.1)

где r⁽ⁿ⁾₁ - n-я порядковая статистика в выборке экстремумов; N - объем выборки экстремумов.

Эта оценка будет надежной, если разность между соседними минимальными взаимными расстояниями r^(m)₁ и r^(m+1)₁ мала.

Таким образом, после оценки характеристического значения v как порядковой статистики необходимость в вычислении третьего центрального момента (или асимметрии) отпадает.

Далее заметим, что минимальное взаимное расстояние в выборке экстремумов

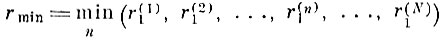
уже дает некоторое указание на величину нижнего предела, но в силу малости объема выборки {r^(N)₁} разность

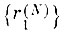
может оказаться довольно большой. Поэтому величину ε (или разность) следует оценивать как функцию объема выборки экстремумов.

Для этого рассмотрим точное выборочное распределение минимума среди минимумов (т. е. первой порядковой статистики в выборке экстремумов):

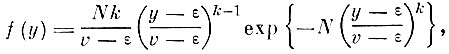(3.I.2)

где значения параметров, входящих в (3. I. 2), те же, что и в распределении (3. 2. 1).

При k > 1 у этого распределения существует мода - наиболее вероятное значение минимума среди минимумов^*. Дифференцируя (3. 2. 1) и приравнивая нулю производную, можно получить выражение для моды r̃₁ как функцию параметров v, k, ε и объема выборки экстремумов N. Из этого выражения определяем нижний предел ε:

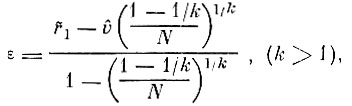(3. I. 3)

где r̃₁ - мода (наиболее вероятное значение распределения (3.1.2).

Остается теперь получить выборочные оценки параметра k и моды r̃₁ и ввести их в (3.1.3).

^* (Заметим, что в практических приложениях, как правило, k>1; если же k≤1, то вместо моды можно использовать какую-либо другую центральную характеристику. )

Из распределения (3.2.1) (см. § 3.2) можно получить, что нормированная разность нижнего предела ε и характеристического значения v равна

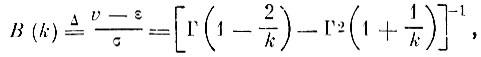(3.I.4)

где σ - среднеквадратичное отклонение экстремумов; В (k) - нормированная разность параметров v и ε; Г(t) - гамма-функция.

Функция В (k) затабулирована в [3.2]. Подставляя (3.1.3) в (3.1.4), получим уравнение, из которого уже можно оценить значение параметра k:

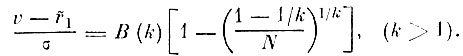(3.I.5)

Для этого в левую часть (3. I. 5) вводятся выборочные оценки характеристического значения v̂ (из 3.1.1), среднеквадратичного отклонения σ̂ выборки экстремумов и моды r̃₁, которую заменяют на наблюдаемый минимум r_min.

Значение k̂, полученное как решение уравнения (3. I. 5), вводится в (3. 1.3). Таким образом, точечная оценка меры не пересекаемости образов имеет вид

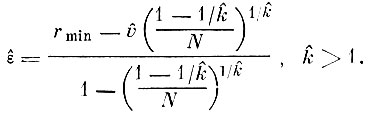(3.I.6)

Легко показать, что эта оценка является состоятельной и асимптотически не смещенной.

Перейдем теперь к построению доверительного интервала для минимального расстояния между образами. Введем нормированную переменную

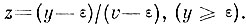
Тогда распределение нормированного минимума среди минимумов имеет вид

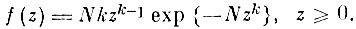(3.I.7)

Нижний предел для нормированной переменной равен нулю. Доверительный интервал для первой порядковой статистики z₁ в нормированной выборке экстремумов запишем в виде

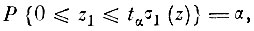(3.I.8)

где

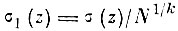
дисперсия нормированного минимума среди минимумов; σ(z) - дисперсия нормированных экстремумов; t_α - коэффициент ширины доверительного интервала; α - доверительная вероятность.

Решая уравнение

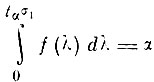
относительно t_α, получим

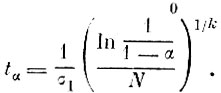(3.I.9)

Произведя замену

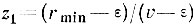
в (3. I. 8) и вводя туда значение t_α, получим доверительный интервал для ε

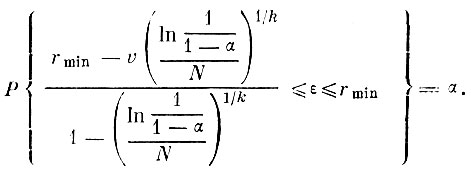
В действительности значения параметров v и k нам неизвестны, мы можем вычислить лишь их оценки v̂ и k̂ (как это показано ранее). Поэтому полученный доверительный интервал является фактически условным доверительным интервалом

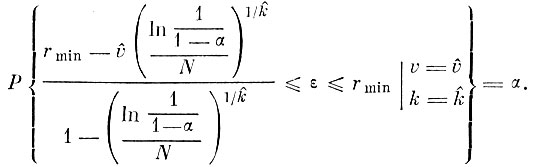(3.I.10)

Сделаем теперь несколько замечаний относительно влияния размерности пространства на оценку меры не пересекаемости образов. Непосредственно процедура получения оценки ε не зависит от размерности пространства, так как оперирует с выборкой одномерных величин - экстремальных взаимных расстояний. Однако исходная функция распределения F(r) взаимных расстояний, если бы она была получена теоретически по многомерным распределениям образов, в явном виде зависела бы от размерности пространства (как, например, распределение модуля многомерного вектора). Соответственно и поведение "левого хвоста" этой функции распределения зависит от размерности пространства. Таким образом, зависимость оценки ε от размерности пространства проявляется лишь косвенно и статистически через выборку взаимных расстояний между классами.