§ 3.4. Расчетный пример

Для проверки изложенной методики и алгоритмов оценки меры не пересекаемости образов были рассчитаны два примера.

Первый пример носит искусственный характер, второй - взят из реальной задачи (опознание 11 слов) с целью получения оценки метрической близости рассматриваемых образов в пространстве признаков (см. главу VIII).

В первом искусственном примере датчиком случайных чисел генерировались точки на плоскости для десяти не- пересекающихся "образов" с равномерным распределением в заданных контурах. Контуры "образов" № 5 и 8 показаны на рис. 3.2. Каждый образ был представлен 50 независимыми реализациями.

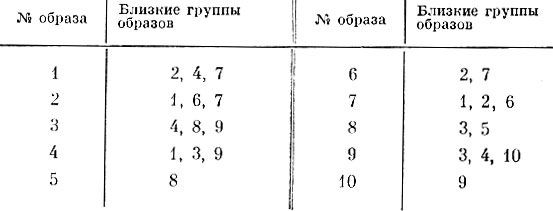
Таблица 3-1

Затем по изложенному в § 3.3 алгоритму было выделено множество взаимных расстояний между близкими группами "образов". Ближайшие группы образов представлены в табл. 3-1.

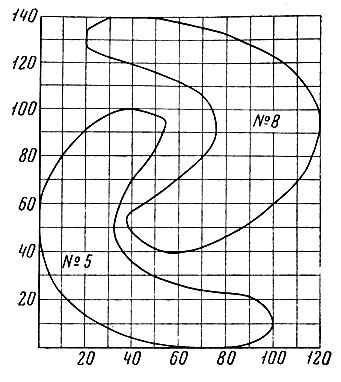
3.2. Заданные оболочки

Выборка взаимных расстояний между близкими группами "образов" (всего оказалось 4793 не повторяющихся взаимных расстояний) разбивалась поровну на 50 групп. В каждой группе фиксировалось только наименьшее взаимное расстояние.

Таким образом было получено 50 минимальных выборочных расстояний, значения которых приведены в табл. 3-2.

По методике, изложенной в приложении, были получены точечные и интервальные оценки величины ε. Эти оценки оказались равными

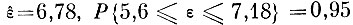
(условных единиц).

Действительное значение минимального расстояния между "образами" равно 6,95 условных единиц (между "образами" № 5 и 8), т. е. полученные оценки дают хорошее представление о реальной величине ε.

Во втором примере при оценке метрической близости образов в найденном пространстве признаков точечная оценка ε = 4,84 оказалась весьма близкой к минимальному выборочному расстоянию между реализациями образов (r_min = 6). Однако интервальная оценка оказалась слишком грубой:

Слишком широкий доверительный интервал обусловлен тем, что выборка взаимных расстояний между близкими группами образов была весьма небольшой. (Рассматривалось и образов - одиннадцать слов по 40 реализаций на каждый образ.)

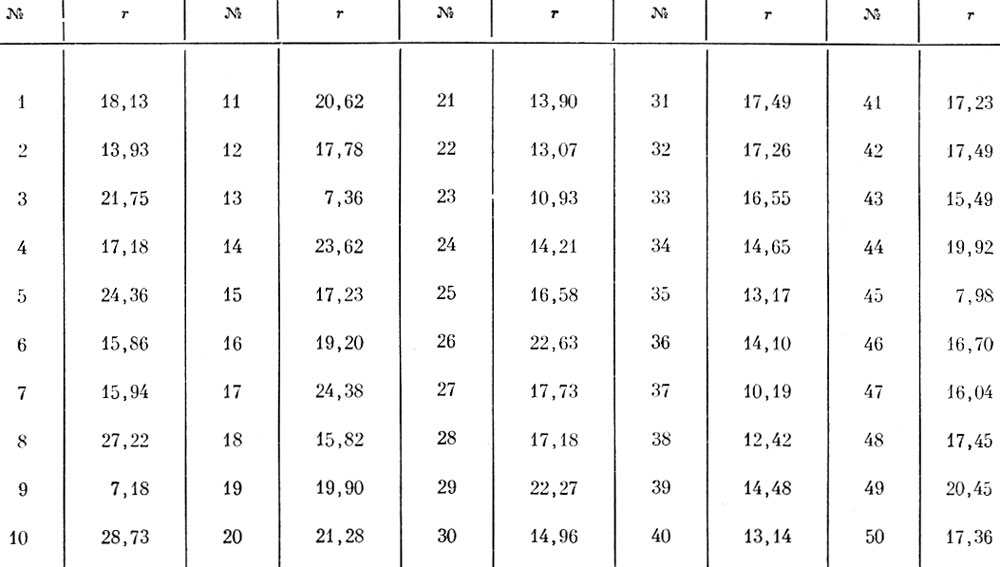
Таблица 3-2