§ 4.4. Создание системы признаков но взвешенному дискриминантному критерию

Недостатком простого дискриминантного критерия является то, что находимые по нему признаки, обеспечивая для векторов, соединяющих центры тяжести образов, малую среднеквадратичную ошибку аппроксимации, будут в первую очередь учитывать различия между "далекими" образами. Это происходит из-за того, что при среднеквадратичной аппроксимации векторов направления координатных осей разложения в большей степени зависят не только от ориентации векторов в исходном пространстве, но и от квадрата их нормы.

Действительно, при оптимизации простого дискриминантного критерия признаки находятся как собственные векторы матрицы ковариации центров тяжести (см. приложение 4.1). Элементы этой матрицы, получаемые путем суммирования произведений пар координат всех центров тяжести, квадратично зависят от расстояний между центрами тяжести образов. Из-за этого величины элементов ковариационной матрицы обусловлены в основном центрами тяжести, далеко отстоящими друг от друга. Отсюда и ориентация собственных векторов ковариационной матрицы, соответствующих наибольшим собственным числам, тяготеет к направлениям векторов, соединяющих наиболее "далекие" пары центров тяжести образов. В результате после отбрасывания последних признаков, соответствующих наименьшим собственным числам, достаточно малая ошибка аппроксимации (получаемая для векторов, соединяющих центры тяжести в среднем) распределена по парам центров тяжести так, что для "близких" пар образов она достигает больших величин, а для "далеких" пар- малых величин.

С другой стороны, интуитивно ясно, что в пространстве признаков в первую очередь необходимо обеспечить различие именно между "близкими" парами образов. Что касается векторов, соединяющих центры тяжести "далеких" образов, то они при этом могут быть аппроксимированы достаточно грубо.

Чтобы направления признаков зависели преимущественно от близко отстоящих образов, необходимо изменить матрицу ковариации так, чтобы ее элементы обусловливались в основном реализациями наиболее близких друг к другу образов. Этого можно достигнуть введением некоторой весовой функции, резко увеличивающейся с уменьшением расстояния между образами.

Таким образом, введение в простой дискриминантный критерий весовой функции, зависящей от норм векторов, соединяющих центры тяжести образов, является его естественным улучшением. При этом весовая функция выбирается так, что векторам, соединяющим центры тяжести "близких" образов, приписывается большой вес, а векторам, соединяющим центры тяжести далеких образов, - малый вес.

Признаки, вносящие наибольший вклад в разложение, будут теперь направлены так, чтобы сохранить разделимость близких пар образов. Это во многих случаях позволяет существенно уменьшить число признаков, необходимое для разделения образов, по сравнению с простым дискриминантным критерием.

Заметим, что такая система признаков создает также благоприятные условия для построения решающего правила: число эталонов для "близких" пар образов не должно" заметно увеличиваться, так как разделимость этих образов из-за введения весовой функции практически не ухудшается по сравнению с разделимостью в исходном пространстве. Для "далеких" образов, как показали эксперименты, несмотря на некоторое уменьшение расстояния между ними, разделимость остается такой, что в решающем правиле достаточно использовать только по одному эталону.

Таким образом, общее число эталонов, характеризующее сложность решающего правила, должно оказаться близким к минимально возможному.

По взвешенному дискриминантному критерию после преобразования U^T, нормирующего меру внутриклассового разброса реализаций, находится система из минимального числа признаков, в которой суммарная взвешенная дисперсия векторов, соединяющих центры тяжести образов, была бы не менее заданной величины.

В формальной постановке задача выглядит следующим образом:

Найти систему векторов {β_j}, минимизирующую функционал

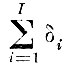
при ограничениях

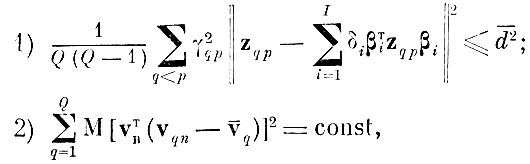(4.4.1)

где

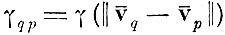
значение весовой функции^* для образов q и р.

^* (Легко видеть, что простой дискриминантный критерий является частным случаем взвешенного дискриминантного критерия, когда весовая функция

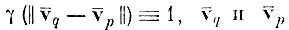
центры тяжести образов q и р после нормирующего преобразования U^T. Введение весовой функции требует в процессе оптимизации признаков рассматривать все пары центров тяжести образов, что усложняет процесс вычислений.)

Вопрос о выборе оптимальной весовой функции подлежит дополнительному исследованию. Некоторые соображения по выбору весовой функции приводятся в главе VIII, где в экспериментах была использована инверсная весовая функция

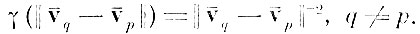
Алгоритм нахождения системы линейных признаков но взвешенному дискриминантному критерию приводится в приложении 4.IV.