§ 4.3. Создание системы признаков по простому дискриминантному критерию

Аппроксимационный критерий, обсуждаемый в предыдущем параграфе, не вполне адекватен задаче опознания образов. Признаки, находимые по этому критерию,

пр одолжают нести избыточную информацию об опознаваемых объектах, ненужную для разделения их на классы.

Для опознания при нахождении признаков желательно сохранять в описании только различия между образами пусть даже за счет большей погрешности в смысле среднеквадратичной ошибки аппроксимации.

Один из критериев, назовем его простым дискриминантным, который несколько сложнее аппроксимационного, но зато несколько ближе к оптимальному, может быть сформулирован следующим образом.

Найти подпространство минимальной размерности (систему признаков), в котором при нормированной внутриклассовой дисперсии межклассовая дисперсия была бы не менее заданной величины.

Другими словами, найти подпространство минимальной размерности, в котором расстояния (в среднем) между реализациями были "малыми" для точек "своего" класса и "большими" для точек разных классов.

В качестве усредненной меры внутриклассового разброса точек здесь принимается оценка среднего квадрата отклонения реализаций от центров тяжести своих образов (внутриклассовая дисперсия). А в качестве меры межклассового различия - оценка среднего квадрата расстояния между реализациями различных образов (межклассовая дисперсия), что эквивалентно [4. 10] дисперсии центров тяжести образов^*.

^* (Такая эквивалентность для более сложных критериев (см. ниже) отсутствует. )

Для нахождения признаков по этому критерию могут быть предложены различные методы [4.6; 4.10].

Целесообразно сначала совершить линейное преобразование U^T (типа косого сжатия), которое нормирует в среднем для всех образов среднеквадратичное отклонение реализаций от своих центров тяжести. Затем методом главных компонент [4.4. ] находится минимальное число признаков, обеспечивающих заданную величину среднеквадратичной ошибки аппроксимации центров тяжести образов (в искаженном первым преобразованием пространстве).

В этом случае задача нахождения разделяющих признаков совпадает с задачей дискриминантного анализа для случая нескольких выборок [4. 6] в многомерной статистике. В формальной постановке задача после перехода в пространство V может быть записана следующим образом.

Найти систему векторов {β_j}, минимизирующую функционал

при ограничениях

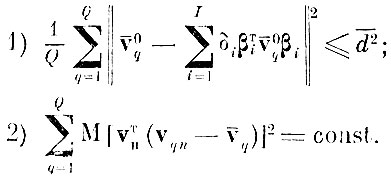(4.3.1)

По простому дискриминантному критерию находится такой ортонормированный базис, в котором при постоянном внутриклассовом разбросе мера межклассового различия - сумма дисперсий центров тяжести, - оставаясь неизменной, перераспределена по осям (признакам) наиболее неравномерно^*.

^* (Признаки β_j заданы в базисе пространства V = U^TX. Признаки w_j, соответствующие векторам β_j и выраженные в базисе пространства исходного описания X, могут быть записаны в виде w_j = Uβ_j.)

По первой оси дисперсия центров тяжести максимальна, по второй - максимальна среди всех оставшихся и т. д. Поэтому при отбрасывании (I-J) признаков, соответствующих наименьшим дисперсиям центров тяжести, среднеквадратичное расстояние между центрами тяжести уменьшается на минимальную величину. Так как среднеквадратичное отклонение реализаций относительно своих центров тяжести постоянно (в среднем для всех образов), то при отбрасывании (I-J) признаков на минимальную величину уменьшается и среднеквадратичное расстояние между точками различных образов.

Обоснования к алгоритму нахождения системы признаков по простому дискриминантному критерию приводятся в приложении 4.1.

Дискриминантный критерий, оперирующий с центрами тяжести образов, адекватен тем задачам опознания, для которых преобразование U^T, нормирующее в среднем разброс реализаций внутри образов, нормирует также разброс реализаций внутри каждого образа относительно любой возможной оси. При этом реализации каждого образа группируются в шаре вокруг своего центра тяжести. Тогда пространство признаков, хорошее в смысле разделения центров тяжести, также хорошо и для разделения реализаций различных образов^*.

Таким образом, при создании признаков по центрам тяжести вопрос о нахождении нормирующего преобразования U^T является весьма важным. На практике иногда бывает целесообразным производить нормирующее преобразование для нескольких групп наиболее близких и одинаково ориентированных образов, а затем уже по дискриминантному критерию искать разделяющие признаки для центров тяжести каждой группы (см. главу VIII, § 8.3).

Алгоритм нахождения нормирующего преобразования U^T излагается в приложении 4.II.

В приложении 4.III излагается алгоритм нахождения системы признаков по простому дискриминантному критерию.

^* (Применяемый метод эталонов (см. главу VI) позволяет реализовать решающую функцию любой сложности, используя при этом минимальное число аппаратурных единиц. При выполнении этих условий решающее правило будет наиболее простым и число эталонов, выполиеныых в метрике l₂, будет равно числу образов.)