§ 4.7. Создание системы признаков по взвешенному одномерному дискриминантному критерию

Ввиду того, что решающее правило, выполненное из набора параллелепипедов с гранями, ориентированными по координатным осям (см. главу VI о решающем правиле в метрике с), реализуется при помощи аналоговой аппаратуры наиболее просто, представляет интерес согласовать критерий оптимизации линейных признаков с решающим правилом этого типа. В этом случае каждый признак в отдельности должен обладать хорошими одномерными разделительными свойствами и разделять не повторяющиеся части выборки образов.

Заметим, что система признаков, обеспечивающая одномерную разделимость образов с порогом d*, обеспечивает также и многомерную разделимость образов с порогом, не меньшим, чем d*. (Обратное утверждение, вообще говоря, неверно.) Число признаков, обеспечивающих одномерную разделимость образов, как правило, несколько больше, чем число признаков, оптимизированных по многомерным дискриминантным критериям. Однако этот недостаток системы одномерных признаков компенсируется чрезвычайной простотой реализации решающего правила в метрике с.

Для нахождения системы одномерных признаков можно использовать аппарат дискриминантного анализа. При этом по тем же соображениям, что в § 4.4, целесообразно в критерий оптимизации ввести весовую функцию, зависящую от расстояния между образами в пространстве исходных параметров. В этом случае мерой качества первого признака является величина взвешенного среднеквадратичного расстояния между проекциями на него всех реализаций различных образов. Мерой качества j-го признака является величина взвешенного среднеквадратичного расстояния между проекциями на него тех реализаций различных образов, которые одномерно не разделились с некоторым заданным порогом d*₀ по всем предыдущим признакам

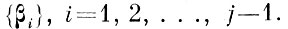
Для сокращения перебора, как и в § 4.4-4.6, предлагается сначала найти одномерные признаки для основной массы реализаций, т. е. находить признаки для разделения центров тяжести, а затем для реализаций, которые не разделились предыдущими признаками.

В формальной постановке взвешенный одномерный дискриминантный критерий можно записать в следующем виде (запись дана для центров тяжести, для реализаций образов изменяются лишь некоторые индексы). (Список обозначений см. на стр. 62-64).

Признаки находятся последовательно. На j-м шаге находится признак β_j из условия

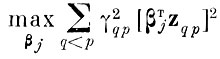
для тех z_qp, для которых

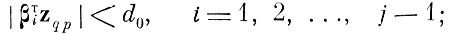(4.7.1)

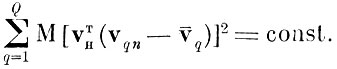
Алгоритм оптимизации признаков по взвешенному одномерному дискриминантному критерию приводится в приложении 4.VII.