§ 4.8. Создание системы признаков по одномерному детерминистскому критерию

Рассмотренные в § 4.4, 4.5, 4.7 алгоритмы оптимизации системы признаков использовали в различных модификациях аппарат дискриминантного анализа [4.6].

В настоящем параграфе излагается метод нахождения системы одномерных признаков, согласованных с решающим правилом в метрике с, с помощью другого математического аппарата. В отличие от одномерного взвешенного дискриминантного критерия оптимизации, при котором признаки ищутся последовательно, предложенный способ позволяет найти систему из минимального числа одномерных признаков сразу.

Задача ставится следующим образом: найти систему из минимального числа одномерно разделяющих признаков, обеспечивающих расстояние в метрике с для каждой пары реализаций различных образов не меньше некоторой величины d*₀ (величина d*₀ выбирается меньше минимального расстояния между реализациями образов, измеренного в метрике l₂ в исходном пространстве).

Для сокращения перебора признаки по этому критерию, как и ранее, могут находиться в два этапа: сначала находится система признаков для разделения центров тяжести образов, а затем для разделения не разделившихся реализаций.

В формальной записи для центров тяжести одномерный детерминистский критерий выглядит следующим образом.

Найти систему векторов

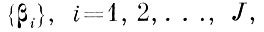
такую, чтобы их число j было минимальным, и для любой пары образов

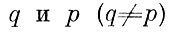
выполнялось условие

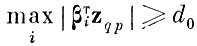(4.8.1)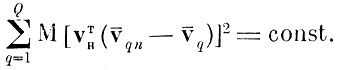

В формулировке (4. 8. 1) задача нахождения признаков является задачей частично-целочисленного линейного программирования.

Если выбор признаков β_j ограничить конечным множеством векторов, играющих роль возможных претендентов "на право называться" признаком, задача нахождения минимального числа признаков может быть приближенно решена с помощью методов минимизации дизъюнктивных нормальных форм булевых функций.

На первом шаге в качестве претендентов на признаки рассматривается весь набор нормированных векторов, соединяющих центры тяжести различных образов.

Для нахождения минимально необходимого количества признаков среди выбранных при сохранении условия разделимости предлагается следующая процедура.

Составляется матрица скалярных произведений, строки которой соответствуют номерам возможных признаков, а столбцы - номерам векторов, соединяющих пары центров тяжести. Элементы матрицы скалярных произведений заменяются единицами и нулями в зависимости от того, оказались ли они больше или меньше заданного порога d₀. Полученная двоичная матрица минимизируется построчно при условии, что в каждом столбце матрицы остается хотя бы одна единица. Тем самым находится минимальное число признаков (из данного набора), обеспечивающих расстояние в метрике с между центрами тяжести не менее заданного порогового значения.

На втором шаге в качестве претендентов на признаки рассматриваются векторы, соединяющие пары реализаций разных образов, которые не разделились с порогом d*] по признакам, найденным для центров тяжести.

Для оставшихся реализаций аналогичным образом составляется двоичная матрица (с порогом

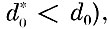
которая минимизируется построчно с помощью алгоритма минимизации дизъюнктивных нормальных форм булевых функций.

Так как алгоритм нахождения системы признаков по одномерному детерминистскому критерию ясен из текста, то в приложении он не приводится.