Приложение 4. I. Обоснование алгоритма нахождения системы признаков по простому дискриминантному критерию

Задача оптимизации признаков, записанная в (4.3. 1), может быть решена в два этапа:

1) находится линейное преобразование U^T, нормирующее внутриклассовую дисперсию (ограничение 2 в (4, 3, 1));

2) в пространстве V = U^TX находится система из минимального числа признаков {β_j}, удовлетворяющая 1 в (4. 3. 1).

Найдем линейное преобразование U^T для нормировки описания относительно внутриклассовой дисперсии.

Составим внутриклассовую матрицу ковариации R, которую определим как Q

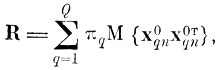(4.I.1)

где g = 1, ..., Q - номер образа; π_q- априорная вероятность появления q-то образа;

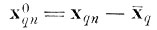
центрированный случайный вектор-столбец, соответствующий n-й реализации д-го образа^*.

^* (Наряду с вектором x_qn ниже будет рассмотрен вектор х_n, являющийся элементом множества реализаций всего алфавита образов (в отличие от вектора x_qn, который является элементом q-го образа).)

Нетрудно видеть, что если матрица ковариации случайного вектора - единичная, то дисперсия этого вектора по любой координатной оси не зависит от направления этой оси.

Действительно, диагональные элементы этой матрицы являются дисперсиями случайного вектора по соответствующим осям исходной системы координат. При преобразовании вектора а в вектор b меняются направления выбранных осей исходной системы координат, а диагональные элементы матрицы ковариации вектора b дают значения дисперсий по соответствующим осям новой системы координат.

Если матрица ковариации случайного вектора а является единичной, то любое ортогональное преобразование С^т над случайным вектором а снова дает единичную матрицу, т. е. если

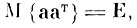
где

Е - единичная матрица, и b = С^та, где С^Т = С^-1, то

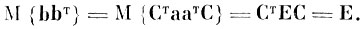(4.I.2)

Так как ортогональное преобразование Ст произвольно, а матрица ковариации случайного вектора а единичная, то дисперсия этого вектора по любой координатной оси не зависит от направления этой оси.

Найдем нормирующее преобразование U^T, которое приводит внутриклассовую матрицу ковариации^* R к единичной матрице Е. Для этого сначала с помощью ортогонального преобразования А^т диагонализируем матрицу R (строки матрицы А^т являются собственными векторами матрицы R, а диагональные элементы матрицы А - ее собственными числами)

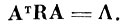(4.I.3)

Затем преобразуем матрицу А к единичной матрице

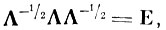(4.I.4)

где

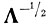
диагональная матрица, обратная матрице

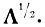
При этом случайный вектор

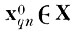
перейдет в случайный вектор

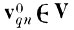
при помощи преобразования

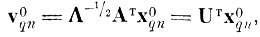(4.I.5)

а случайный вектор

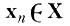
этим же преобразованием будет переведен в вектор

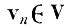
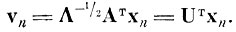(4.I.6)

Таким образом, линейное преобразование U^T, нормирующее описание относительно внутриклассовой дисперсии, заключается в последовательном применении двух операций: поворота, осуществляемого с помощью матрицы ортогонального преобразования А^т, и линейного сжатия по осям, осуществляемого с помощью диагональной матрицы

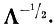
Перейдем к нахождению системы из минимального числа признаков {β_j}, аппроксимирующих векторы, соединяющие центры тяжести образов с заданной среднеквадратичной ошибкой d̄₂ в пространстве V.

Известно [4.3, 4.7, 4.8], что разложение, аппроксимирующее случайный вектор v∈V с минимальной среднеквадратичной ошибкой, является разложением по собственным векторам матрицы ковариации

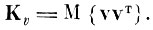
Действительно, рассмотрим I-мерный центрированный случайный вектор v и обозначим в I-мерном пространстве V некоторый линейнонезависимый базис

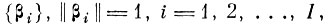
в котором и будем искать приближение вектора V, вектором У размерности J<I.

Излагаемое здесь доказательство упрощено, так как при опознании не требуется восстанавливать вектор У в исходном пространстве. Полное доказательство оптимальных свойств аппроксимации случайного вектора с минимальной среднеквадратичной ошибкой имеется в [4.4-4.8].

Будем изменять базис {β_j} так, чтобы среднеквадратичная ошибка аппроксимации случайного вектора v, получаемая при отбрасывании I - J координатных осей

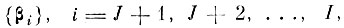
была минимальной (для удобства записи векторы β_i переупорядочены так, что тем индексам i, для которых δ_i = 0, присвоены номера J+1, J+2, .....,I). Т. е., учитывая ограничение 1 в (4,3.1), найдем

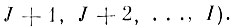(4.I.7)

где

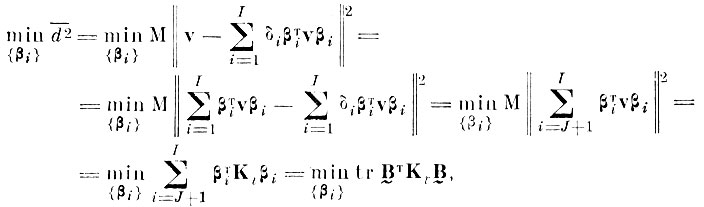
матрица ковариации центрированного случайного вектора v; В̰ - прямоугольная матрица из I строк и (I - J) столбцов, которыми являются нормированные векторы

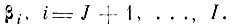
Решаем задачу на минимум с помощью множителей Лагранжа

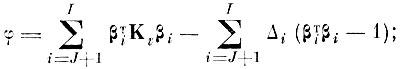(4.I.8)

или в матричной форме

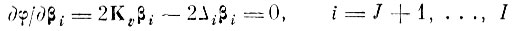(4.I.9)

где Δ̰-диагональная матрица

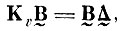(4.I.10)

Из (4. 1.9, 4.1.10) видно, что А является усеченной сверху матрицей собственных чисел + ковариационной матрицы, а В̰ - усеченной сверху матрицей соответствующих собственных векторов β_i, i = J + 1,....,I

В силу того, что матрица ковариации является симметричной и положительно определенной, ее собственные векторы {β_j} - ортогональны, т. е. матрица В̰ является усеченной сверху ортогональной матрицей.

Из (4.I.7) с учетом (4.I.10) и

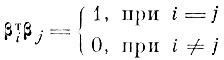(4.I.11)

Если все I собственных значений матрицы К_v упорядочить по величине, т. е. так, чтобы

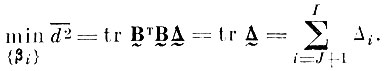
то выражение (4.1.11) имеет место, если в первой части его стоят собственные числа начиная с номера J+1.

Обозначим усеченную снизу матрицу собственных векторов матрицы К_v соответствующих наибольшим собственным числам

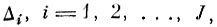
через В̰.

Нетрудно показать, что преобразование В̰ можно использовать для нахождения минимального числа координатных осей (признаков), обеспечивающих заданную среднеквадратичную ошибку аппроксимации d̄₂.

Действительно, пусть d̄₂ задана и лежит в пределах

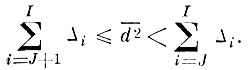(4.I.12)

Тогда, согласно доказанному, J первых членов разложения дают ошибку

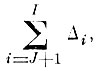
что обеспечивает заданное приближение.

Это число членов является и минимально возможным, так как из предположения, что заданную ошибку обеспечивает J - 1 член, следовало бы, что J - 1 член может дать ошибку, меньшую

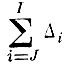
в то время как по доказанному минимальная ошибка, которую может дать J - 1 член, равна

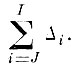
Указанное свойство верно для любого J.

Итак, чтобы найти систему из минимального числа признаков {β_j}, аппроксимирующих векторы, соединяющие центры тяжести образов с заданной среднеквадратичной ошибкой d̄₂, необходимо найти собственные векторы матрицы ковариации центров тяжести (в пространстве с нормированной внутриклассовой Дисперсией) и оставить те из них, которые соответствуют J наибольшим собственным числам.

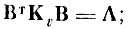(4.I.13)

где

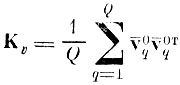
матрица ковариации центров тяжести;

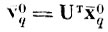
центрированный центр тяжести образа после нормирующего преобразования; В^т - транспонированная матрица ортогонального преобразования, строки которой являются собственными векторами матрицы К_v; Λ - матрица упорядоченных по величине собственных чисел матрицы К_t.

Размерность пространства признаков J выбирается из условия

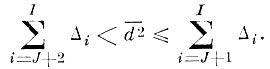(4.I.14)

Таким образом, окончательное преобразование исходного описания X в пространство простых дискриминантных признаков Ỹ записывается в виде

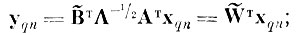(4.I.15)

где В̃^т - усеченная снизу матрица собственных векторов матрицы К_v, строки которой являются собственными векторами, соответствующими J первым наибольшим собственным числам; W̃^T-прямоугольная матрица признаков из J строк.

В некоторых случаях матрицу линейного преобразования W̃^T удобнее находить другим способом, который рассмотрим ниже.

Нетрудно видеть, что (4.1. 13) с учетом (4.1. 5) может быть записано в виде

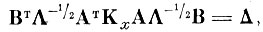(4.I.16)

где

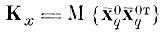
матрица ковариации центров тяжести в пространстве исходного описания X.

Перепишем (4.I.4) с учетом (4.I.3)

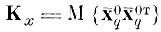(4.I.17)

Отсюда

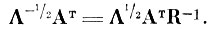(4.I.18)

Перепишем (4.1. 16) с учетом (4.I.18)

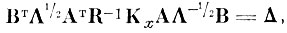(4.I.19)

или с учетом (4.1. 15)

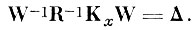(4.I.20)

Из уравнения (4.1.19) видно, что строки матрицы W^T являются собственными векторами матрицы

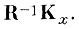
Из (4.1. 20) искомое преобразование W̃^T, отображающее пространство исходного описания X в сокращенное пространство Ỹ, получается путем вычеркивания из матрицы W^T собственных

векторов, соответствующих (I - J) наименьшим собственным числам Δ_i.

Профиль каждой девушки на https://kandalakshasm.date полностью анонимен.