Приложение 4. II. Алгоритм нахождения преобразования UТ, нормирующего меру внутриклассового разброса

Ввиду того, что для большинства процедур оптимизации системы признаков требуется предварительно производить нормирование внутриклассового разброса, алгоритм нахождения нормирующего преобразования U^T вынесен в отдельное приложение. Исходный массив состоит из Q образов по N_q реализации для q-го образа (всего

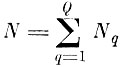
реализаций всех образов).

Требуется найти преобразование U^T, обеспечивающее для

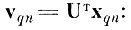
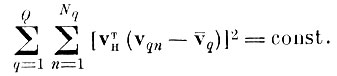(4.II.1)

Согласно (4.1.5), нормирующее преобразование

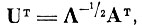(4.II.2)

где

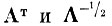
(4.I.3) находятся из

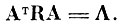(4.II.3)

1. Найти усредненную внутриклассовую матрицу ковариации

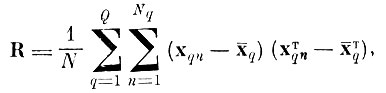(4.II.4)

2. Найти матрицы собственных векторов и собственных чисел матрицы R (4. II. 3) [4.14].

3. Найти погрешность max|δλ|, зависящую от объема учебной выборки.

4. Проверить информативность собственных векторов матрицы R, соответствующих собственным числам, сравнимым по порядку величины с погрешностью max|δλ|. Если для i-го собственного вектора

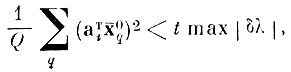
то i-й собственный вектор исключается из матрицы А^т, а соответствующее ему соответственное число λ_i исключается из матрицы Λ (t - заданное число).

5. Получить матрицу Λ₀, элементы которой определяются по элементам матрицы Λ и величине возможной ошибки max|δλ|,

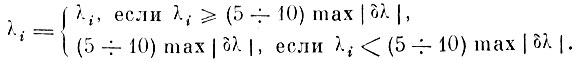
6. Найти матрицу

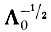
(по матрице Λ₀).

7. Произвести умножение матриц

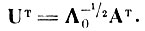(4.II.5)