Приложение 4. III. Алгоритм оптимизации признаков по простому дискриминантному критерию

Требуется найти систему из минимального числа признаков

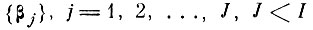
при ограничении

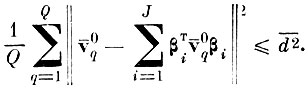(4.III.1)

1. Совершить нормирующее преобразование U^т над центрами тяжести образов х̄_q, найденными в J-мерном пространстве исходного описания X

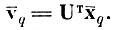(4. III. 2)

2. Вычислить матрицу ковариации преобразованных центров тяжести в пространстве V

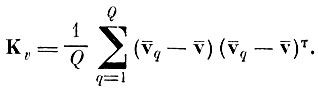(4. III. 3)

3. Вычислить матрицу ортогонального преобразования В^т, которая диагонализирует матрицу ковариации К_v

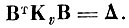(4. III. 4)

4. Переупорядочить собственные векторы (строки матрицы В^т) в соответствии с величинами собственных чисел

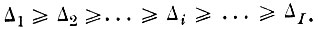
5. Выделить матрицу В̃^т, соответствующую первым J собственным числам, где J находится согласно (4. I. 14).

Окончательно преобразование исходного описания X в пространство простых дискриминантных признаков Y записывается в виде

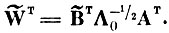(4. III. 5)