Приложение 4. V. Алгоритм нахождения дополнительных признаков

Дополнительные признаки ищутся для тех реализаций, расстояние между которыми в сокращенном J-мерном пространстве признаков, найденном для разделения центров тяжести, меньше d*₀. Введем следующие обозначения:

признаки, найденные для центров тяжести, в координатах пространства

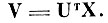
Первые J признаков {β_j} обеспечивают разделимость центров тяжести с заданным порогом d̄₂;

дополнительные признаки

в координатах пространства

найденные для не разделившихся реализаций. Первые К признаков {χ_j} обеспечивают разделимость этих реализаций с заданным порогом d̄*²,

t = 1, . . ., Т - индекс, соответствующий номеру нары реализаций различных образов, не разделившихся в J-мерном базисе {β_j} с порогом d*₀.

Формально задача нахождения дополнительных признаков может быть записана следующим образом.

Найти систему векторов {χ_j}, минимизирующую функционал

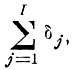
при ограничении

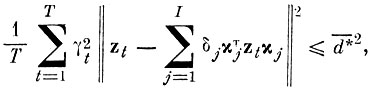(4.V.1)

где z_t - вектор, соединяющий t-ю пару реализаций образов, расстояние между которыми в J-мерном базисе {β_j} меньше d*₀.

1. Совершить преобразование массива учебной выборки в полное J-мерное пространство признаков, найденных по взвешенному дискриминантному критерию для центров тяжести образов

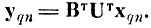(4.V.2)

2. Вычислить взвешенную матрицу ковариации K_z для реализаций, не разделившихся с порогом d₀*, в подпространстве J первых признаков {β_i}, найденных для центров тяжести,

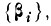(4.V.3)

Для вычисления матрицы К_z предлагается следующий алгоритм.

2.1). Построить J-мерный габаритный эталон в метрике с для q-го образа (q = 1,...., Q - 1). Координаты габаритного эталона находятся по формуле

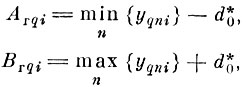(4.V.4)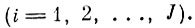

2.2). Вызвать массив образа

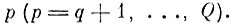
2.3). Проверить, попадает ли m-я реализация (m = 1, ... . . ., N_p) образа р внутрь габаритного эталона образа q.

Реализация не попадает в габаритный эталон образа q, если

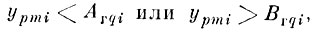(4.V.5)

хотя бы для одного i = 1, . . ., J.

2.4). Если реализация y_pm не попадает в габаритный эталон, перейти к пункту 2.9. В противном случае выполнять пункт 2.5.

2.5) . Вычислить расстояние^* в J-мерном подпространстве от реализации y_pm. попавшей в габаритный эталон образа q, до реализации y_qn

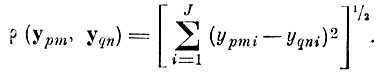(4.V.6)

2.6) . Если

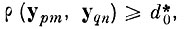
перейти к пункту

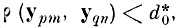
перейти к пункту 2. 7.

2.7) . Вычислить для данной пары реализаций

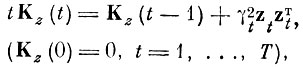(4.V.7)

Т - количество обращений к пункту 8.

2.8) . Перейти к пункту 2.5 (цикл по n ≤ N_q);

2.9) . Перейти к пункту 2.4 (цикл по m≤N_p);

2.10) . Перейти к пункту 2.2 (цикл по р ≤ Q);

2.11) . Перейти к пункту 2.1 (цикл по q ≤ Q - 1).

^* (Если желательно получить систему признаков, обеспечивающую одномерные свойства разделимости, то )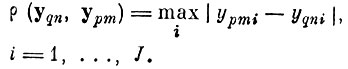

3. Вычислить матрицу ортогонального преобразования С^т, которая диагонализирует матрицу К_z

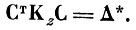(4.V.8)

4. Переупорядочить собственные векторы χ^T_j, (строки матрицы С^т) в соответствии с величинами собственных чисел

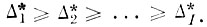
5. Выделить матрицу С̃^т, соответствующую первым К собственным числам Δ_j*, где К находится согласно (4.1. 14).

6. Составить матрицу признаков^* W̃_T, первые J строк которой находятся согласно (см. приложение 4. IV).

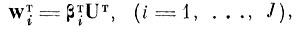(4.V.9)

а строки начиная с J + 1 до К находятся согласно

(4.V.10)

^* (В случае построения решающего правила в метрике l₂ следует произвести ортогонализацию векторов {β_i}, (i = 1, . . ., J) и {χ_j}, (j = 1,....,K))