Приложение 4. IX. О некоторых связях между критериями качества дискриминантных признаков и матрицами ковариации R и К, вычисленными в пространстве исходного описания

Пусть

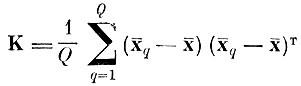
межклассовая ковариации (матрица ковариации центров тяжести) и

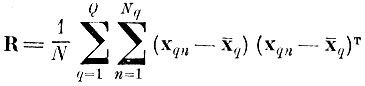
усредненная (по всем внутриклассовая матрица ковариации, вычисленная в исходном пространстве X.

Определитель |R| характеризует усредненное внутриклассовое рассеяние реализаций образов x_qn относительно своих центров тяжести x̄_q. Определитель |К + R| соответственно характеризует рассеяние реализаций всех образов относительно общего центра тяжести х̄.

Рассмотрим предварительно тривиальный случай, когда все образы лежат в маломерном подпространстве и, следовательно, заведомо существует сильно вырожденное линейное преобразование W̃^T, отображающее с полным сохранением разделимости образов J-мерное исходное описание в I-мерном подпространстве признаков (J<I). Очевидно, что при этом |K + R| = 0, а ранг матрицы K + R определяет число признаков J. В этом случае размерность описания может быть понижена до J признаков, сохраняющих разделимость, с помощью алгоритма нахождения признаков по аппроксимационному критерию.

Рассмотрим теперь наиболее вероятный в многоклассовых задачах опознания случай, когда |R| ≠ 0, т. е. образы не лежат в подпространстве пространства исходного описания.

В этом случае величина tr Δ (где Δ матрица собственных чисел определяется уравнением |К - ΔR| = 0) характеризует средний квадрат расстояний между центрами тяжести образов в полном пространстве признаков, найденных по простому дискриминантному критерию

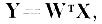
в котором все образы в среднем приведены к шару единичного радиуса (см. приложение 4.1).

Очевидно, что существование эффективной системы признаков (с точки зрения разделимости образов в среднем см. § 4.3), найденной по простому дискриминантному критерию, определяется величиной

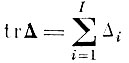
и степенью неравномерности распределения Δ_i.

В частности, если матрица Δ вырожденная, т. е. все собственные числа Δ_i начиная с некоторого номера i = J + 1 равны нулю, то заведомо существует J-мерное подпространство Ỹ, в котором разделимость образов полностью сохранена по сравнению с I-мерным пространством исходного описания X. Более точно это означает, что отношение

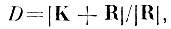
вычисленное для выборки в I-мерном пространстве исходного описания X и в J-мерном пространстве признаков Ỹ, равны друг другу.

Для получения качественной оценки неравномерности распределения собственных чисел Δ_i по матрицам R и К, вычисленным в пространстве исходного описания X, рассмотрим некоторые соотношения.

Выразим величину tr Δ через матрицы ковариации R и К.

Для этого, заметим что

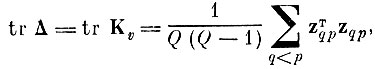
где

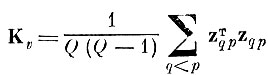
в пространстве

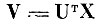
с нормированной внутриклассовой дисперсией (см. приложение 4.1);

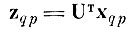
вектор, соединяющий центры тяжести образов q и р в пространстве V, а х_qр - соответствующий ему вектор в пространстве X.

Так как

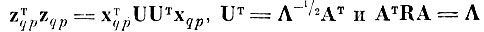
(см. приложение 4.1), то

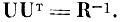
Тогда

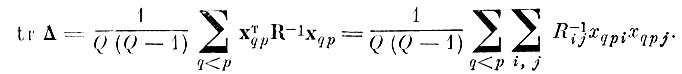
Учитывая теперь, что

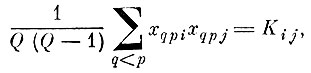
окончательно получим

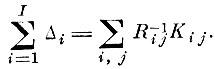(4.IX.1)

Рассмотрим отношение определителей

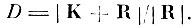
Так как матрица внутриклассовой ковариации R (по предположению) положительно определенная, а матрица межклассовой ковариации К положительно полуопределенная, то существует вещественная неособенная матрица W такая, что

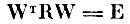
и

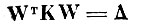
(Δ - диагональная матрица). Тогда величина D может быть представлена в виде

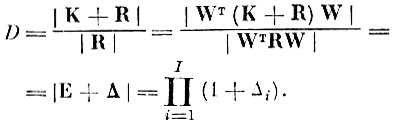(4.IX.2)

Выражения (4. IX. I) и (4. IX. 2) заменим соответственно соотношениями

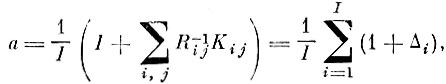(4.IХ.3)

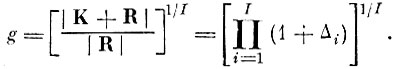
В силу известного неравенства между средним арифметическим и средним геометрическим всегда справедливо

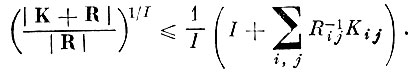(4.IX.4)

Для оценки неравномерности распределения собственных чисел Δ_i рассмотрим отношение

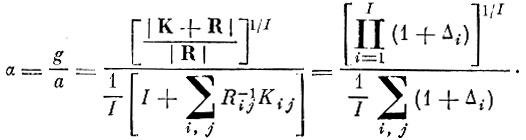(4.IX.5)

Очевидно, что при α→1 спектр стремится к равномерному (

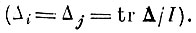
С другой стороны, для данного tr Δ величина α ограничена

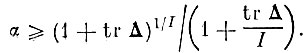
Этот случай соответствует наиболее неравномерному распределению собственных чисел Δ_i, когда наибольшее собственное число

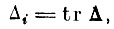
а все остальные

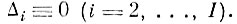
Таким образом, имеет место двустороннее неравенство

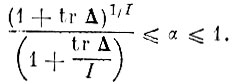(4.IX.6)

Чем меньше значение α, тем более неравномерно распределены собственные числа Δ_i и тем больше вероятность того, что основная доля полного среднеквадратического расстояния между образами tr Δ сосредоточена в подпространстве размерности J<I.

Однако величина tr Δ (4. IX. 1), как уже указывалось, характеризует разделимость образов лишь в среднем.

При нахождении системы признаков по взвешенному дискриминантному критерию целесообразно рассматривать не интегральное отношение (4. IX. 2), а отношение вида

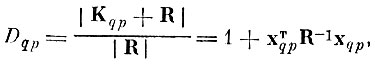(4.IX.7)

Исходя из свойств взвешенного дискриминантного критерия, можно надеяться, что если величина

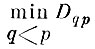
превышает некоторый заданный порог и число относительно близких пар образов равно К, а все остальные пары образов относительно далеки друг от друга, то пространство найденных признаков определяется в основном подпространством, в котором находятся К ближайших образов.