Приложение 4. VIII. К вопросу об устойчивости дискриминантных признаков

Ценность системы признаков, найденных по учебной выборке, существенным образом зависит от того, насколько их разделяющие свойства экстраполируются на экзаменационную выборку.

В этом приложении рассматривается один из возможных способов оценки устойчивости только тех систем признаков, которые

находятся по простому дискриминантному критерию. Вопрос об устойчивости системы признаков, находимых по другим обсуждаемым в этой главе критериям, требует дополнительных исследований. Здесь рассматривается также способ сохранения устойчивости дискриминантных признаков в тех случаях, когда внутриклассовая матрица ковариации плохо обусловлена. Устойчивость признаков, оптимизируемых по аппроксимационному критерию, рассмотрена в работе [4.12].

Систему дискриминантных признаков будем называть устойчивой, если вариация критерия качества системы признаков для различных экзаменационных выборок оказывается достаточно малой. Вариативность критерия качества системы признаков можно характеризовать, например, его дисперсией.

Напомним, что дискриминантные признаки минимизируют метрическую разделимость образов в среднеквадратичном смысле при сохранении в среднем внутриклассового рассеяния реализаций каждого образа. Статистической мерой качества дискриминантных признаков является сумма дисперсий расстояний между проекциями центров тяжести образов па пространство признаков

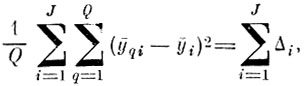(4.VIII.1)

где ȳ_q - центр тяжести образа q в пространстве признаков,

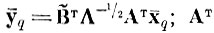
А^Т - матрица (I×I) ортогонального преобразования, строки которой являются собственными векторами внутриклассовой матрицы ковариации

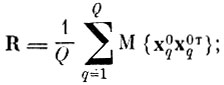
Λ^-1/2 - диагональная матрица, находимая по матрице собственных чисел Λ, внутриклассовой матрицы ковариации R;

В̃^т - прямоугольная матрица J×I собственных векторов матрицы ковариации центров тяжести

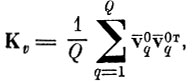
вычисленной после нормирующего преобразования

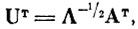
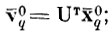
Δ_i - упорядоченные по величине собственные числа матрицы ковариации центров тяжести K_v.

Мерой качества каждого дискриминантного признака (i-й строки матрицы

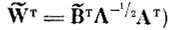
является соответствующее собственное число Δ_i (i = 1, 2, . .,J), показывающее, какой вклад вносит i-й признак в сумму (4. VIII. 1).

Рассмотрим устойчивость меры качества отдельного i-го признака. Очевидно, что если отдельные признаки устойчивы, то устойчива и их сумма.

Мера качества признаков, оптимизируемых по простому дискриминантному критерию, как это видно из (4. VIII. 1) зависит от двух матриц ковариации R̂ и К̂_v, оценки которых R и K_v находятся по конечной учебной выборке.

При последовательной процедуре оптимизации системы признаков (см. приложение 4. I) целесообразно рассмотреть влияние флуктуаций оценок этих матриц на меру качества дискриминантных признаков отдельно. Такое последовательное рас- смотрение степени влияния ошибок выборочных матриц R̂ и К̂_v позволяет в случае плохой обусловленности матрицы R̂ внести некоторые исправления, повышающие устойчивость признаков в целом.

Прежде всего рассмотрим влияние неточности элементов внутриклассовой матрицы ковариации R̂ на определение преобразования U^T, нормирующего меру внутриклассового рассеяния (см. приложение 4. I).

Представим выборочную матрицу ковариации в виде

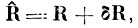(4.VIII.2)

где R - истинная внутриклассовая матрица ковариации; δR - матрица ошибок, обусловленных конечностью объема учебной выборки.

Элементы матрицы δR являются случайными величинами, дисперсия которых уменьшается как О (N^-1) с ростом объема выборки. Собственные числа матрицы R̂ будут также случайными числами, вариацию которых и требуется оценить.

Вариация собственного числа матрицы R̂ может быть представлена [4. 13, 4. 14]:

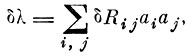(4.VIII.3)

где

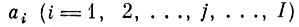
i-я координата собственного вектора матрицы

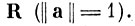
Можно дать несколько оценок сверху для вариации δλ.

Детерминистская оценка [4.13]

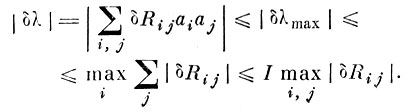(4.VIII.4)

Эта оценка является весьма грубой.

Как видно из (4.VIII.4), она может превосходить максимальное собственное число δλ_max матрицы ошибок δλ и растет с увеличением порядка матрицы (размерности пространства).

Статистическая оценка [4. 12, 4. 13]. Подсчитаем дисперсию δλ

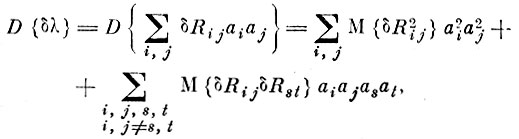(4.VIII.5)

где

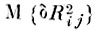
дисперсия элемента матрицы R̂; М {δR_ijδR_st} - ковариация элементов матрицы.

Если элементы δR_ij и δR_st матрицы ошибок независимы, то, очевидно,

(4.VIII.6)

т. e. в этом случае дисперсия ошибки собственного числа не зависит от порядка матрицы R̂.

Если же элементы матрицы ошибок коррелировапы, то в общем случае получить не слишком грубую оценку сверху для дисперсии (4.VIII.5) очень трудно.

Грубая оценка сверху для дисперсии (4.VIII.5) может быть получена с помощью неравенства Коши-Буняковского

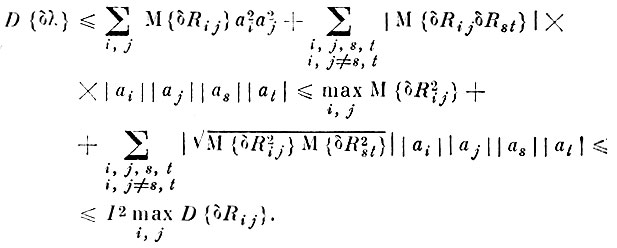(4.VIII.7)

Оценка (4.VIII.7) no порядку величины совпадает с детерминистской оценкой (4.VIII.4).

Все же можно значительно улучшить оценку вариации собственных чисел, если использовать некоторые практические соображения о характере матрицы R̂.

Часто элементы матрицы ковариации убывают по абсолютной величине достаточно быстро по мере удаления от главной диагонали. Это означает, что при некотором расстояний по индексам |i-j| ≥ m коэффициент корреляции становится достаточно малым и не превышает по модулю некоторой величины μ.

Так, например, если координаты i и j связаны с квантованием по времени некоторых случайных физических процессов, то убывание корреляции между отсчетами во многих случаях [4. 15] хорошо аппроксимируется выражением

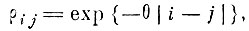(4.VIII.8)

где θ - декремент затухания.

Аналогичные соображения можно привести, если координаты i и j связаны с квантованием процесса по частоте или с квантованием по другим физическим параметрам с учетом инерционности реальных измерений.

Таким образом, если матрица ковариации R имеет достаточно выраженный квазидиагональный вид, то и корреляцию ошибок δR_ij и δR_st можно считать незначительной, когда эти элементы расположены в матрице относительно далеко друг от друга:

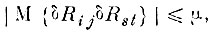(4.VIII.9)

если

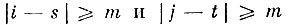
одновременно.

Ограничение (4.VIII.9) позволяет уточнить оценку дисперсии собственного числа матрицы R̂

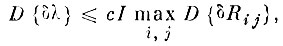(4.VIII.10)

где

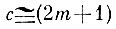
(при достаточно малом отношении m/I).

Рассмотрим теперь преобразование

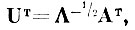
нормирующее меру внутриклассового разброса, с учетом флуктуаций спектра выборочной матрицы ковариации.

Если природа образов такова, что спектр матрицы внутриклассового рассеяния R̂ достаточно неравномерен, то при переходе в пространство, в котором внутриклассовая дисперсия нормирована, могут возникать значительные искажения требуемой деформации образов. В самом деле, в этом случае выборочные флуктуации δλ спектра R̂ могут оказаться, начиная с некоторого номера λ_k, сравнимыми с истинными значениями компонент спектра. Тогда операция нормирования внутриклассового рассеивания (умножение на матрицу Λ^-1/2) будет в указанном смысле неустойчивой.

Это обстоятельство может осложняться еще и тем, что именно те собственные векторы, которые соответствуют сильно флуктуирующим оценкам спектра, могут оказаться и наиболее информативными в смысле разделимости образов.

Такая ситуация соответствует тому, что сами образы лежат в параллельных (или почти параллельных) подпространствах. Поэтому при последовательной оптимизации дискриминантных признаков невозможно отбросить "малозначимые" и неустойчивые оси (как это делается в главных компонентах), так как "с водой можно выплеснуть ребенка".

Для сохранения устойчивости дискриминантных признаков в этом случае следует отказаться от требования полной нормировки внутриклассовой дисперсии и произвести лишь частичную нормировку. С этой целью малые компоненты спектра матрицы R̂, оценки которых сравнимы с погрешностью их определения, заменяются на последнее по порядку устойчивое число, т. е. вместо последовательности

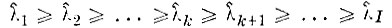
используется последовательность

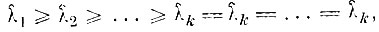
где

Частичная нормировка преобразует учебную выборку не к шару в среднем по всем образам, а к квазиэллипсоиду. Зато преобразование нормирования становится значительно более устойчивым от выборки к выборке.

Естественно, что при этом максимизация среднеквадратичного расстояния между центрами тяжести в пространстве

становится не совсем адекватной простому дискриминантному критерию оптимизации системы признаков, причем неадекватность тем больше, чем больше собственных чисел, сравнимых с величиной ошибки δλ.

Отметим, что плохая обусловленность внутриклассовой матрицы ковариации R может быть вызвана двумя различными причинами: либо все образы находятся ("почти" находятся) в подпространстве меньшей размерности, либо образы лежат в "параллельных" подпространствах.

В первом случае для упрощения последующей процедуры оптимизации признаков целесообразно сразу сократить размерность пространства V, в котором нормирована внутриклассовая дисперсия, исключив собственные векторы, соответствующие собственным числам, сравнимым но величине с ошибкой их определения. Во втором случае сокращать размерность пространства нельзя, так как именно те собственные векторы, соответствующие малым собственным числам, могут оказаться наиболее информативными для разделения образов. Различия между этими двумя случаями легко установить, измеряя расстояние между центрами тяжести образов вдоль собственных векторов с малыми значениями собственных чисел.

Перейдем теперь к оценке вариации собственных чисел выборочной матрицы ковариации центров тяжести K_v

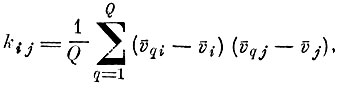(4.VIII.11)

где v̄_qi-i-я координата центра тяжести q-го образа; v̄_i-i-я координата общего центра тяжести всех образов; Q - количество образов.

Так как число образов конечно, то статистическая природа этой матрицы проявляется лишь в том, что векторы v̄_q и v̄ определены по конечной выборке, т. е. с некоторой погрешностью.

Положим

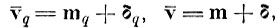
причем случайные векторы ошибок δ_q и δ распределены нормально (так же как и случайные выборочные векторы v̄_q и v̄) [4. 6]. Не нарушая общности, положим также, что т = 0, т. е. что общий центр тяжести совпадает с началом координат.

Представим выборочную матрицу ковариации в виде

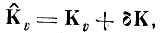(4.VIII.12)

где δК - матрица ошибок; K_v - истинная матрица ковариации центров тяжести.

Тогда, предполагая, что в пространстве, в котором внутривыборочное рассеяние нормировано, координаты случайных векторов ошибок δ_qi и δ_qj не коррелированы. Из (4.VIII.7), пренебрегая членами второго порядка малости, получим выражение для дисперсии собственных чисел

(4.VIII.13)

Используя теперь условие нормальности вектора ошибки, легко получить стандартным способом оценку для вариации собственных чисел, выраженную через дисперсии оценок центров тяжести [4.6, 4.12].

Нигде в предыдущем изложении мы не учитывали неточность определения собственных векторов матриц R и К. Ясно, что при неточном определении соответствующих собственных векторов величина критерия качества не достигает своего максимального значения.

Однако очевидно, что более важным является собственно стабильность критерия на некоторые фиксированные направления (признаки), несущественно отличающиеся от оптимальных направлений. Другими словами, разделяющие свойства найденной по учебной выборке, системы признаков должны сохраняться и на всевозможных экзаменационных выборках.

Именно поэтому особое внимание было уделено в этом приложении устойчивости собственных чисел, которые в дискриминантных признаках являются их критерием качества.