§ 5.2. Сокращение размерности исходного описания с использованием информации о пространстве признаков

После того как по полному исходному описанию найдена система из минимального числа признаков, сохраняющая ε-непересекаемость образов, возникает вопрос, все ли исходные параметры одинаково важны для найденной совокупности признаков, и если нет, то какие из них и сколько можно исключить из исходного описания (или заменить линейными комбинациями оставшихся), чтобы при этом сохранилась требуемая разделимость образов.

Возможность решения этой задачи основана на следующих соображениях. Если размерность пространства разделяющих признаков (см. главу IV) значительно меньше размерности исходного описания и величина критерия качества такой системы мало отличается от величины критерия для полной системы признаков, то это означает, что исходное описание содержит в себе значительную избыточность, устранение которой мало повлияет на разделимость образов.

Другими словами, если величина критерия отброшенной части признаков не превышает некоторой величины 0, малой по сравнению с полной величиной критерия, это означает существование почти линейной зависимости некоторой части исходных параметров с точки зрения разделимости образов.

Описанные в главе IV алгоритмы нахождения системы линейных признаков оперируют с векторами взаимных расстояний между реализациями различных образов. Малость величины критерия отброшенной части признаков в этом случае означает сильную коррелированность некоторой части координат векторов взаимных расстояний.

Для устранения избыточных признаков рассмотрим существующие почти линейные связи. Замена почти линейной зависимости точной линейной зависимостью для части параметров исходного описания не может привести к сильному ухудшению разделимости в силу непрерывности оператора признаков.

Заметим, что замена некоторой части исходных параметров линейной комбинацией оставшихся эквивалентна их исключению, так как линейную зависимость координат исходного описания по отношению к векторам взаимных расстояний между образами можно учесть в операторе признаков, произведя в нем соответствующие изменения.

Первую задачу сокращения исходного описания с точки зрения наблюдателя, находящегося в пространстве признаков, можно содержательно сформулировать следующим образом.

Найти минимальное подмножество независимых исходных параметров, для которых величина критерия разделимости не сильно отличается от величины критерия для полного описания.

В качестве меры, контролирующей степень ухудшения разделимости образов, можно выбрать функционал вида

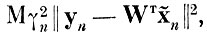(5.2.1)

содержащий информацию о найденном по полному исходному описанию пространстве признаков в виде оператора (матрицы) системы признаков W^T. В формуле (5.2. 1) y_n - n-й вектор взаимных расстояний между реализациями различных образов в пространстве признаков Y; х̃_n - n-й вектор взаимных расстояний в исходном пространстве X, у которого часть координат заменена линейными комбинациями оставшихся; γ_n - весовая функция, зависящая от нормы вектора; W^T - матрица (оператор) системы признаков, найденных по полному описанию X.

Теперь задачу сокращения размерности описания можно формально записать так:

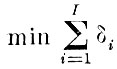
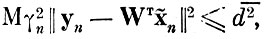(5.2.2)

d̄² - заданная величина отклонения.

Введение весовой функции

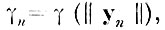
подобно тому как это производилось при оптимизации системы признаков (см. главу IV), позволяет при сокращении размерности исходного описания прежде всего сохранить разделимость между близкими парами образов за счет некоторого "сближения" далеких образов.

Точное решение поставленной задачи (в силу ее целочисленного характера) связано с перебором подмножеств исходных параметров и для больших размерностей описания весьма трудоемко.

В приложении 5.1 приведены экономичные субоптимальные процедуры, в различной степени разрешающие противоречие между близостью к оптимальному решению и сложностью вычислительных алгоритмов.