§ 5.3. Сокращение размерности исходного описания но простому дискриминантному критерию

В настоящем параграфе решается задача сокращения числа координат исходного описания с точки зрения наблюдателя, находящегося в исходном пространстве.

Специфика задач опознания при таком подходе большей частью такова, что наблюдатель стремится сократить число координат до такой величины, при которой еще возможно разделение образов.

В случае использования информации о подпространстве признаков (см. § 5.2) удается минимизировать исходное описание методом, адекватным тому критерию, по которому оптимизируется система признаков, причем сам критерий может быть весьма сложен.

При отсутствии информации о подпространстве признаков задача минимизации исходного описания для сложных критериев оказывается слишком трудоемкой. В связи с этим в настоящем параграфе рассматривается способ сокращения исходного описания только по простому дискриминантному критерию (см. § 4.3), который может быть записан в более общем виде, пригодном также и для поставленной задачи, следующим образом [5.13]:

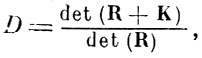(5.3.1)

где К - внутриклассовая матрица ковариации; К - межклассовая матрица ковариации.

Выражение (5. 3. 1) обладает рядом свойств, которые позволяют применить его в качестве критерия эффективности исходных параметров. Это - возможность работы с большим алфавитом образов (матрицы R и К составляются для совокупности всех рассматриваемых образов). Критерий (5.3.1) является монотонно возрастающей функцией от среднеквадратичного расстояния между образами, т. е. отражает разделяющудо способность параметров исходного описания. Кроме того, критерий (5.3.1) монотонно убывает при сокращении числа исходных параметров (см. приложение 5.2), т. е. эффективность части параметров не может быть выше эффективности полной совокупности.

Сформулируем вторую задачу минимизации размерности исходного описания. Найти минимальную совокупность параметров исходного описания, такую что величина критерия для оставшихся параметров окажется не меньше заданной величины.

В формальной постановке задача может быть записана так:

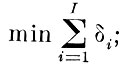(5. 3. 2)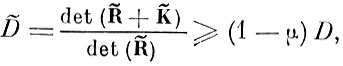

где δ_i = 0, если i-й параметр исключается из X; δ_i = 1, если i-й параметр остается; D - значение критерия для исходной совокупности параметров, т. е. в полном пространстве X; D̃ - значение критерия для оставшихся параметров; R, К - матрицы R и К для оставшихся параметров, т. е. в сокращенном пространстве X̃; μ - заданный относительный дефект критерия качества при отбрасывании некоторой части исходных параметров; I - число параметров (размерность) исходного описания X.

Оптимальное решение поставленной задачи в силу целочисленного ее характера состоит в переборе (полном или направленном) всех возможных подмножеств исходных параметров.

Очевидно, что полный перебор всех подмножеств параметров исходного описания для нахождения наилучшего подмножества возможен лишь для небольших размерностей пространства исходного описания.

В случае большого числа исходных параметров приходится прибегать к приближенным методам решения поставленной задачи.

В качестве первого приближения можно воспользоваться субоптимальным алгоритмом решения задачи, который состоит из нескольких последовательных шагов, причем на каждом шаге исключается тот параметр, который дает минимальное уменьшение величины D̃. Процесс исключения параметров прекращается, когда величина D̃ уменьшится до заданной величины и при дополнительном ограничивающем условии сохранения ε-непересекаемости.

Количество вычислительных операций для данного алгоритма сокращается в

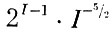
раз по сравнению с полным перебором. Оценочные формулы этого параграфа имеют асимптотический характер, т. е. верны для больших значений I. Вывод этих формул дан в приложении 5. III.

При весьма большом числе исходных параметров приходится отказаться и от субоптимального алгоритма сокращения числа исходных параметров и идти по пути дальнейшего упрощения алгоритма за счет еще большего отхода от оптимального решения.

Одним из возможных алгоритмов такого рода является следующий алгоритм.

Каждый из I исходных параметров по одному исключается из полной совокупности параметров и каждый раз подсчитывается значение D̃. Затем параметры нумеруются в порядке возрастания значений D̃. Первые J параметров, для которых величина критерия окажется не меньше заданной величины, и составляют искомое сокращенное подпространство. Для этого алгоритма количество вычислительных операций сокращается в 0,3I раза по сравнению с предыдущим алгоритмом.