Глава шестая. Детерминированный метод построения решающего правила (метод эталонов)

§ 6.1. Введение

Наиболее традиционным вопросом в опознании образов является этап построения решающей функции.

Способ построения решающей функции зависит от количества априорной информации об образах.

В рамках детерминированно-статистического подхода построение решающего правила производится в условиях, когда многомерные распределения образов неизвестны, а объем учебной выборки на образ недостаточен для получения оценок распределений. На практике дело, как правило, осложняется еще и довольно большим алфавитом образов. С другой стороны, существенное облегчение при построении решающего правила обусловлено тем, что ε-непересекаемость образов, постулируемая в пространстве исходного описания, сохраняется в пространстве признаков (см. главу II).

С такой ситуацией можно встретиться при решении многих практических задач опознания образов, к которым относятся некоторые задачи опознания речевых и зрительных образов, а также ряд задач технической диагностики.

В этих условиях при построении решающего правила желательно использовать всю информацию, заключенную в учебной выборке, рассматривая каждую учебную реализацию как представителя некоторого подмножества "близких" реализаций экзаменационной выборки. Кроме того, из-за большого алфавита образов необходимо принимать меры к тому, чтобы построенное решающее правило было по возможности более простым и могло быть реализовано при помощи стандартных блоков.

Описываемый ниже детерминированный метод построения решающего правила с дополнительной минимизацией числа признаков позволяет реализовать решающую функцию любой сложности с помощью минимального числа аппаратурных единиц (заданного типа) при условии нулевой ошибки опознания на учебной выборке [6.1-6.4].

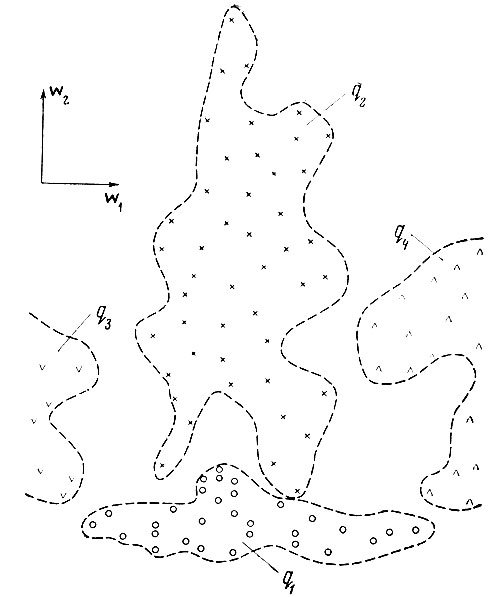
6.1. Пример учебной выборки образов q₁, q₂, q₃, q₄

Коррекция полученного решающего правила и прогноз величины ошибок на экзамене рассматриваются в главе VII.