§ 6.2. Идея метода эталонов

Пусть области классов, заданные своими учебными выборками в пространстве признаков, не пересекаются. Этот случай иллюстрируется рис. 6.1, на котором в двумерном пространстве признаков w₁ и w₂ изображены четыре образа - q₁, q₂, q₃, q₄. Каждый образ задается конечным

числом реализаций учебной выборки. Точка, представляющая каждую реализацию, определяется совокупностью значений выбранных признаков. На рис. 6.1 интуитивные границы образов обозначены пунктирной линией. Границы, установленные автоматом (см. ниже), могут существенно отличаться от интуитивных, что видно из рис. 6.2.

Области на рис. 6.1 односвязны. Это не обязательно, вообще говоря, область образа может быть многосвязной.

Идея метода эталонов основана на введении так называемых "функций принадлежности" (см. приложение 6.1).

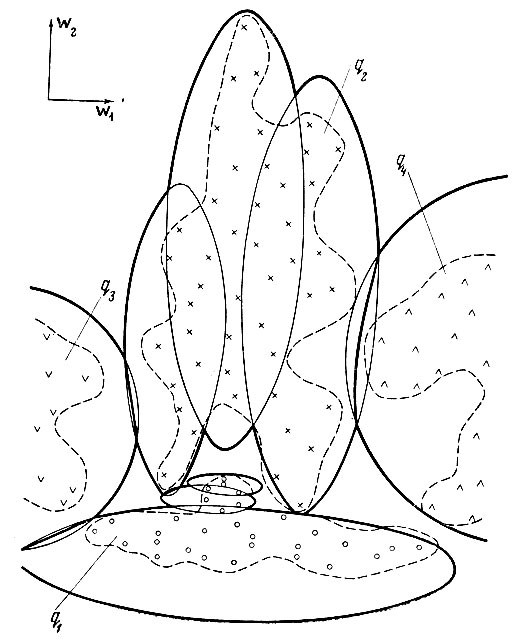
6.2. Эталоны и границы между образами, построенные с использованием функций принадлежности

Функция принадлежности к данной реализации образа определяет меру сходства (в определенной метрике) между произвольной точкой пространства признаков и данной реализацией учебной выборки образа^*. На этой реализации, называемой эталонной, функция принадлежности принимает максимальное значение, равное единице. По мере удаления от реализации функция принадлежности монотонно убывает до нуля, причем скорость ее убывания определяется удаленностью ближайшей реализации "чужих" образов. На всех реализациях учебной выборки "чужих" образов функция принадлежности тождественно должна равняться нулю^**.

^* (Хотя функция принадлежности связана с расстоянием в выбранной метрике, но не удовлетворяет аксиомам метрического пространства. Так, например, может случиться, что первая реализация "принадлежит" ко второй, а вторая реализация "не принадлежит" к первой (см. приложение 6.II).)

^** (В [6. 5] рассматривается случай, когда функция принадлежности на "чужих" реализациях принимает отрицательные значения.)

Введение функций принадлежности к каждой реализации учебной выборки образа позволяет безошибочно опознавать учебную выборку.

Совокупность этих функций определяет так называемую функцию принадлежности к образу (см. приложение 6.1).

На экзамене принятие решения об образе может состоять в определении образа, функция принадлежности к которому на опознаваемой реализации максимальна.

С понятием функции принадлежности тесно связано понятие эталона. Эталон представляет собой замкнутое выпуклое геометрическое тело в многомерном пространстве признаков. Поверхность эталона образована геометрическим местом точек, в которых функция принадлежности обращается в нуль, а форма эталона зависит от принятой для конструирования функции принадлежности метрики.

На рис. 6.2 поверхности эталонов образованы эллипсами различных размеров и ориентации. В многомерном пространстве им соответствуют гиперэллипсоиды (метрика l₂). Отношение осей эталонов каждого образа соответствует отношению максимальных разбросов реализаций данного образа по соответствующим осям (см. § 6.4).

Другим примером эталонов являются гиперпараллелепипеды (метрика с).

Эталон можно рассматривать как квантованную на два уровня функцию принадлежности, принимающую значение 1 на точках, попадающих внутрь эталона, на которых функция принадлежности больше нуля, и значение 0 на точках, находящихся вне эталона.

Использование эталонов вместо непрерывных функций принадлежности упрощает процесс принятия решения, но вместе с тем несколько ограничивает сложность конфигурации области образа.

Так, например, при построении эталонов в метрике l₂ область образа формируется только гиперэллипсоидальными поверхностями. В случае метрики с область образа формируется из "кусков" гиперплоскостей, ориентированных по координатным осям.

Различие состоит еще и в том, что границы между образами, задаваемые с помощью непрерывных функций принадлежности, образуются как геометрическое место точек, на которых значение функций принадлежности к различным образам одинаково. При этом полученные области образов не могут пересекаться. Квантование функции принадлежности на два уровня при переходе к эталонам может привести к тому, что в тех местах, где отсутствуют реализации учебной выборки, сформированные области образов могут пересекаться.

В области пересечения реализации учебной выборки не попадают, однако реализации экзаменационной выборки могут попадать в эти области. В этом случае автомат будет выдавать ответы, которые классифицируются как ошибки типа альтернативной (о типах ошибок при опознании и о методах изменения решающего правила для их уменьшения см. главу VII).

Альтернативные ошибки, появляющиеся за счет пересечения эталонных оболочек образов, могут быть легко исключены, если на границах между образами непрерывные функции принадлежности тождественно равны нулю. Этого можно достигнуть, потребовав, чтобы функция принадлежности принимала значение единица на эталонной реализации данного образа и монотонно убывала до нуля на точках, отстоящих от нее на половину расстояния (в определенной метрике) до ближайшей реализации "чужого" образа. Решающее правило, образованное из функций принадлежности такого типа, полностью соответствует решающему правилу из эталонов.

Таким образом, решающее правило, построенное из непрерывных и квантованных функций принадлежности, позволяет безошибочно опознавать учебную выборку.

Эталоны являются дискретным аналогом непрерывной функции принадлежности.

Возможны два способа построения решающего правила из эталонов, отличающихся наличием и отсутствием областей пересечения эталонных оболочек образов. В обоих случаях внутри эталонных оболочек образов содержатся только реализации учебной выборки "своего" образа. Отличие заключается в том, что в первом случае на экзамене по контрольной выборке возможны альтернативные ошибки, а во втором случае этих ошибок не будет. Другим отличием является то, что минимальное число эталонов (из данного набора), покрывающих учебную выборку "своего" образа и не включающих ни одной реализации других образов, в первом случае будет меньшим, чем во втором.