§ 6.8.2. Минимизация числа признаков при использовании метрики с (первый подход)

В том случае, когда эталоны выполнены в метрике с, задачу дополнительной минимизации числа признаков в обоих подходах удается решить методами поиска минимальных дизъюнктивных нормальных форм булевых функций.

Рассмотрим идею первого подхода к дополнительной минимизации числа найденных признаков для случая, когда эталоны выполнены в метрике с.

В этом случае каждый эталон представляет собой многомерный параллелепипед с гранями, параллельными координатным осям. Реализация попадает внутрь параллелепипеда, если все ее проекции на оси координат находятся внутри всех интервалов по координатным осям, задающих этот параллелепипед. Для установления того, что реализация не попадает внутрь параллелепипеда, достаточно, чтобы хотя бы одна из ее проекций на оси координат находилась вне одного из интервалов параллелепипеда. Если реализация находится вне параллелепипеда, то легко обнаружить, по каким именно координатным осям она не попадает.

Таким образом, каждой реализации, находящейся вне эталона, можно поставить в соответствие номера координат, по которым она не попадает в данный эталон.

Это обстоятельство можно использовать для решения задачи дополнительной минимизации числа признаков методами поиска минимальных дизъюнктивных нормальных форм булевых функций [6.6, 6.7]. При этом для каждого эталона можно составить двоичную матрицу.

Строки матрицы соответствуют номерам осей координат (номерам признаков), а столбцы - номерам реализаций "чужих" образов, которые после минимизации не должны попасть в данный эталон. Элемент матрицы, находящийся на пересечении i-й строки и n-то столбца матрицы, принимает значение единицы, если n-я реализация "чужого" образа не попадает в данный эталон по i-й координате. Элемент матрицы принимает значение нуль, если n-я реализация попадает в данный эталон по i-й координате.

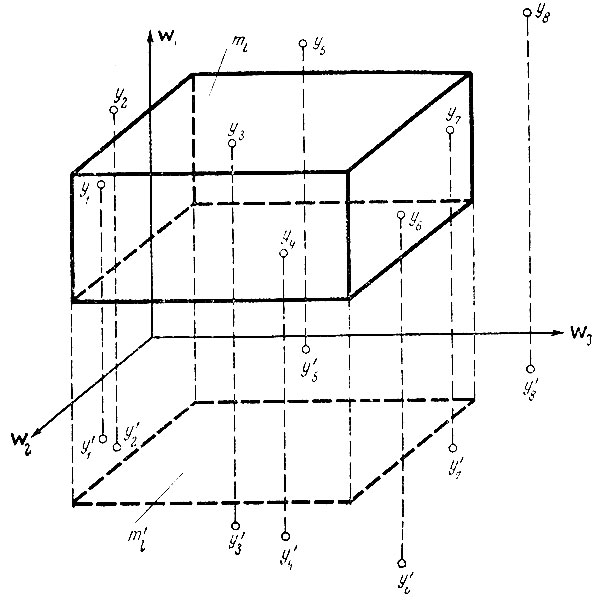
6.7. Реализации образа q̄_l и m-й эталон образа q_l в пространстве признаков (y_n - n-я реализация образа q̄_l, y'_n - проекция n-й реализации образа q̄_l)

Для нахождения минимального числа признаков данного эталона нужно найти минимальное число таких координат, которые в совокупности обеспечили бы расположение всех реализаций выборки "чужих" образов вне данного эталона в пространстве оставшихся координат. Это значит, что нужно найти такое минимальное число строк матрицы, при котором в каждом столбце имелась хотя бы одна единица. Для этого следует минимизировать число строк двоичной матрицы при сохранении по крайней мере одной единицы в каждом столбце.

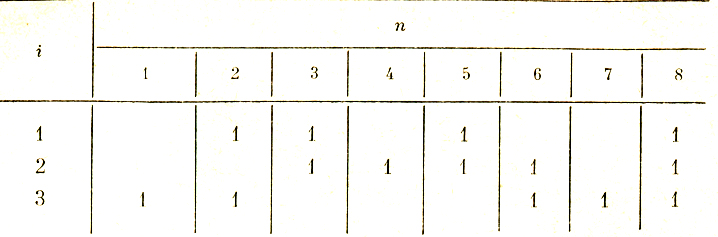
Таблица 6.1

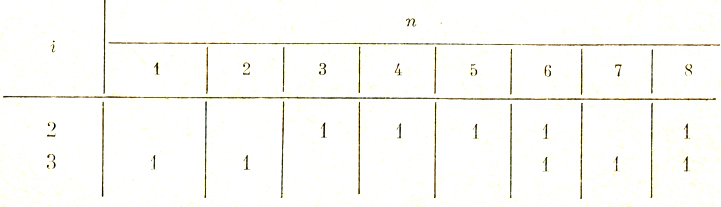
Таблица 6.2

В примере, приведенном на рис. 6.7, реализация y₁ не попадает в трехмерный эталон m_l по координате w₃, реализация y₂ - по координатам w₁ и w₃. На рисунке видно, что проекции всех точек на плоскость w₂w₃ лежат вне прямоугольника m_l, являющегося проекцией эталона.

Тот же результат можно получить путем минимизации матрицы, изображенной в табл. 6.1. При минимизации числа строк этой матрицы получается матрица, изображенная в табл. 6.2, содержащая две строки, которые соответствуют осям координат w₂ и w₃.

Изложение алгоритма первого подхода приведено в приложении 6.IV.