Приложение 6. I. Функция принадлежности

Функция принадлежности η_n (y) к эталонной точке y_n метрического пространства определяется выражением

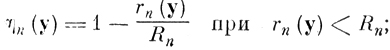
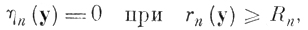(6.I.1)

где y_n, y - точки (векторы) метрического пространства признаков Ỹ; r_n(y) - расстояние между двумя точками y_n и y в выбранной метрике; R_n - положительное число (радиус эталона).

Поверхность эталона с центром в точке y_n определяется как множество точек y, для которых r_n(y) = R_n.

Функция принадлежности а (у) к образу определяется выражением

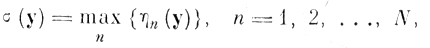(6.I.2)

где максимум берется по всем эталонным реализациям образа.

В конечном (J-мерном) пространстве наиболее распространенный класс метрик - метрики Минковского - записывается в виде

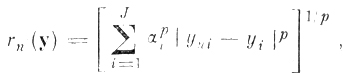(6.I.3)

где р ≥ 1; α_i - коэффициент сжатия по i-й оси; y - вектор с координатами (y₁, y₂, ...., y_J); y_n - вектор с координатами (y_n1, y_n2,....,y_nJ).

В частности, полагая р = 1, 2, . . получаем метрики l₁, l₂, l_∞ = c соответственно:

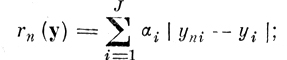(6.I.4)

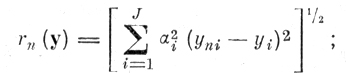(6.I.5)

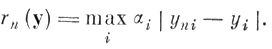(6.I.6)