Приложение 6. II. Алгоритм построения эталонов и минимизация их количества

Пусть в J-мерном пространстве признаков заданы непересекающиеся множества точек, относящиеся к учебным выборкам различных классов (g = 1, 2, . . ., Q}.

Требуется найти покрытие для множества точек класса q, состоящее из минимального числа J-мерных эллипсоидов с осями, параллельными направлениям координат, центрами которых являются реализации учебной выборки класса q.

Для удобства изложения в дальнейшем будем обозначать через q̄ дополнение к подмножеству q.

Алгоритм сводится к следующему:

1. Составляется диагональная матрица линейного преобразования сжатия α_q для точек выборки q.

Элемент матрицы α_qi соответствующий коэффициенту сжатия по i-й координатной оси, находится по формулам

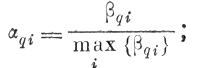(6.II.1a)

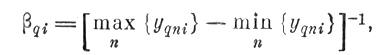(6.II.1б)

Где y_qni - значение i-й координаты n-й реализации образа q.

2. Вычисляется квадратная симметричная матрица взаимных расстояний между реализациями класса q (матрица r_q):

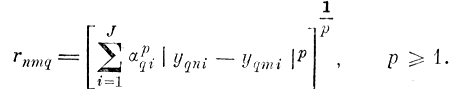(6.II.2)

3. Вычисляется габаритный эталон^* А_qΓ.

а) Для каждой n-й строки матрицы r_q находится максимальный элемент

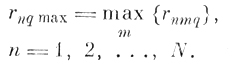(6.II.3)

б) Находится элемент матрицы r_n0qmax, который является минимальным среди максимальных элементов в строках матрицы

в) Центр габаритного эталона A_qΓ совпадает с реализацией под номером n₀, соответствующим номеру строки элемента матрицы r_n0qmax

г) Радиус габаритного эталона определяется по формуле

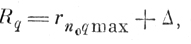(6.II.5)

где Δ - число, учитывающее аппаратурную погрешность.

^* (Пункты 3, 4 предназначены для сокращения операций при вычислении ближайшей "чужой" реализации. При этом результирующее число эталонов несколько увеличивается (см. § 6.6).)

4. Определяются номера реализаций из класса q̄, попавшие в габаритный эталон A_qΓ. Эти реализации удовлетворяют условию

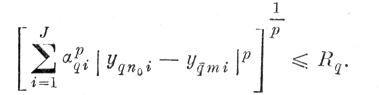(6.II.6)

5. Составляется столбцовая матрица R_q, элементы которой характеризуют минимальное расстояние от каждой реализации класса q до ближайшей реализации подмножества q̄.

а) по формуле (6. II. 7) вычисляется минимальное расстояние от каждой реализации класса q до ближайшей реализации подмножества q̄:

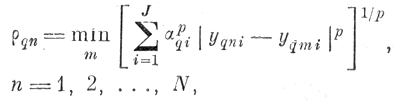(6.II.7)

где y_qni - значение i-й координаты n-реализации образа q;

y_q̄mi - значение i-й координаты m-реализации образа q̄.

В случае выполнении пунктов 3, 4 вместо всех реализаций класса q̄ берутся реализации, получившиеся из пункта 4.

б) По формулам (6. II. 8) вычисляются элементы столбцовой матрицы R_q.

При первом способе построения эталонных оболочек (см. § 6.2) элемент столбцовой матрицы

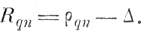(6.II.8a)

При втором способе построения эталонных оболочек элемент столбцовой матрицы

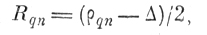(6.11.8б)

где Δ - число, учитывающее аппаратурную погрешность.

6. Вычисляется матрица принадлежности η_q между реализациями образа q

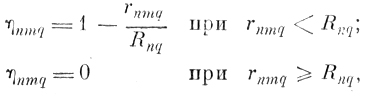(6.II.9)

где n - номер строки матрицы, соответствующий номеру одного из предполагаемых эталонов; m - номер столбца матрицы, соответствующий номеру реализации класса q.

Из (6.II.9) видно, что функция принадлежности η_nmq больше нуля в том случае, если расстояние от n-й реализации класса q до m-й реализации этого же класса меньше (с запасом Δ) расстояния от той же реализации до любой реализации любого другого класса и равно пулю в противном случае.

Матрица η_nmq квадратна, но не симметрична, т. е. η_nmq ≠ η_mnq.

Вполне возможен случай, когда m-я реализация принадлежит к n-й, а n-я реализация не принадлежит к m-й.

7. Находится минимальное число эталонов, достаточное для того, чтобы на всех реализациях учебной выборки класса q значения функций принадлежности были больше нуля.

а) матрица принадлежности η_q заменяется двоичной матрицей принадлежности φ_q.

Элемент двоичной матрицы принадлежности определяется по формуле:

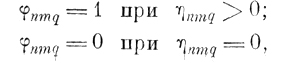(6.II.10)

б) Двоичная матрица принадлежности φ_q минимизируется построчно при помощи стандартных методов поиска минимальных дизъюнктивных нормальных форм булевой алгебры.

При этом номер строки полученной матрицы соответствует реализации, являющейся центром эталона, а радиус эталона равен соответствующему элементу столбцовой матрицы R_q.

Для нахождения минимального числа эталонов в рассматриваемом примере оказалось достаточно выполнить лишь операции поглощения строк и столбцов.

8. В случае, если оказалось, что покрытий, состоящих из минимального числа эталонов, не одно, а несколько, то выбирается одно из них при помощи методов, приведенных в [6. 1].