Приложение 6. VII. Дополнительная минимизация числа признаков методами нелинейного программирования (постановка задачи)

Пусть в J-мерном пространстве найденных признаков с базисом

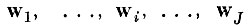
для образов q₁ ,. . ., q_l найдены эталоны в виде J-мерных эллипсоидов с осями, параллельными направлениям базисных векторов.

Требуется для m-го эталона образа q_l найти подпространство

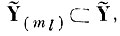
образованное минимальным числом базисных векторов исходного пространства Ỹ, в котором бы в m-й эталон образа q_l не попадало бы ни одной реализации образа q̄_l.

1. Производится линейное преобразование (сжатие) пространства признаков, такое, чтобы в преобразованном пространстве всем эталонам образа q_l соответствовали гиперсферы в обобщенной метрике Минковского:

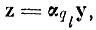(6.VII.1)

где α_ql - диагональная матрица линейного преобразования сжатия, найденная для выборки образа q_l.

При этом границы те-го эталона образа определяются выражением

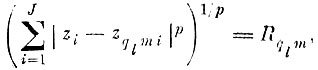(6.VII.2)

где z_i - значение i-и координаты произвольной точки z; z_qlmi- значение i-й координаты центра m-го эталона образа q_l; R_qlm - "радиус эталона" (радиус эталонной гиперсферы).

2. Расстояние между проекцией m-й гиперсферы образа q_l и проекцией реализации выборки образа q̄_l на подпространство

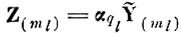
определяется выражением

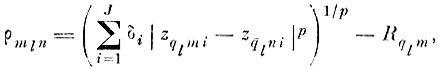(6.VII.3)

где

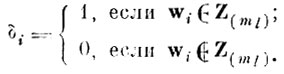(6.VII.4)

Для минимизации числа первичных признаков требуется найти такую совокупность δ_i, которая минимизирует линейную форму

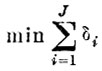(6.VII.4)

при условиях

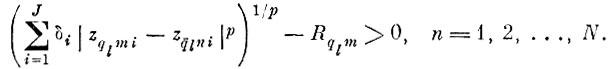(6.VII.5)

Уравнения 6. VII. 4 и 6. VII. 5 являются канонической записью задачи нелинейного программирования с целочисленными решениями.