Приложение 6. VI. Упрощенный алгоритм минимизации числа признаков при использовании метрики с

При первом подходе задача дополнительной минимизации числа признаков может быть сформулирована иначе, чем в приложении 6. IV.

Для m-го эталона образа q_l найти подпространство

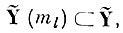
образованное минимальным числом базисных векторов пространства Ỹ, в котором бы m-й эталон образа q̄_l не пересекался ни с одним из эталонов образа <Д. Очевидно, что при этом найденная совокупность признаков заведомо обеспечивает отсутствие в данном эталоне реализаций "чужих" образов. 1. Относительно m-го эталона образа q>_l вычисляется "сокращенная" двоичная матрица

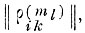
отличающаяся от матрицы

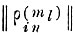
(см. приложение 6. IV) тем, что &-номер столбца матрицы соответствует номеру эталона образа

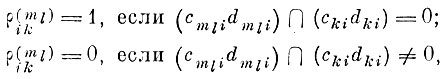(6.VI.1)

где

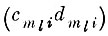
интервал m-го параллелепипеда образа q_l на i-й координатной оси;

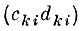
интервал k-го параллелепипеда образа q_l на i-й координатной оси.

2. Затем выполняются пункты 2, 3, 4 приложения 6. IV. Использование "сокращенной" матрицы упрощает процесс вычислений при дополнительной минимизации. Результат, получаемый после минимизации "сокращенной" матрицы, получается близким к оптимальному.

При втором подходе задача дополнительной минимизации числа признаков может быть сформулирована иначе, чем в приложении 6. V.

Требуется:

1) найти подпространство

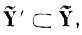
образованное минимальным числом базисных векторов исходного пространства Ỹ, о котором бы эталоны, относящиеся к различным образам, не пересекались;

2) для каждого m-го эталона образа q_l найти подпространство

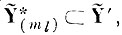
образованное минимальным числом базисных векторов пространства Y', в котором бы m-й эталон образа q_l не пересекался ни с одним из эталонов образа q̄_l.

Такая постановка задачи приводит к составлению "сокращенной" общей матрицы, аналогичной матрице

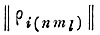
(см. приложение 6. У).

При этом число столбцов общей матрицы значительно сокращается, однако результаты, получаемые после минимизации "сокращенной" матрицы, не являются оптимальными.