§ 7.2. Обсуждение методики статистической коррекции

Сущность метода коррекции заключается в следующем. Эталонные оболочки различных образов корректируются так, что с заданной вероятностью в них не должны попадать реализации "чужих" образов. Этим обеспечивается требуемый уровень ошибок неправильного опознания.

Области альтернативных ошибок получаются при этом только там, где границы между образами сложны и сами образы близки друг к другу. Это вполне естественно, так как ограниченность учебной выборки не позволяет достаточно точно аппроксимировать пограничные области между близкими образами.

Для образов, которые далеки друг от друга, ограниченность учебного материала практически не влияет на их разделимость, так как выпуклые оболочки этих образов не пересекаются, и в этом случае области альтернативных ошибок не образуются.

Область ошибок отказа формируется как дополнение к скорректированным эталонным оболочкам различных образов и областям альтернативных ошибок.

Для осуществления коррекции по независимой контрольной выборке оцениваются две одномерные предельные статистические характеристики:

L(α_L, N) - максимально возможный выброс реализаций за эталонную оболочку "своего" образа с доверительной вероятностью α_Ll

l(α_l, N) -максимально возможное проникновение реализаций в глубь эталонных оболочек "чужих" образов с доверительной вероятностью α_l.

Методика получения оценок этих параметров по конечной контрольной выборке изложена в § 7.3.

После оценки предельных статистических характеристик L (α_L, N) и l(α_l, N) коррекция решающего правила проводится в два шага.

1. Первый шаг процедуры коррекции решающего правила направлен на уменьшение ошибок отказа до некоторой заданной величины β_L. Для этого эталонные оболочки образов (предварительно построенные по учебной выборке) расширяются по всем направлениям в пространстве признаков на величину L (α_L, N) максимально возможного выброса реализаций за эталонную оболочку "своего" образа (см. рис. 7.1) с доверительной вероятностью α_L.

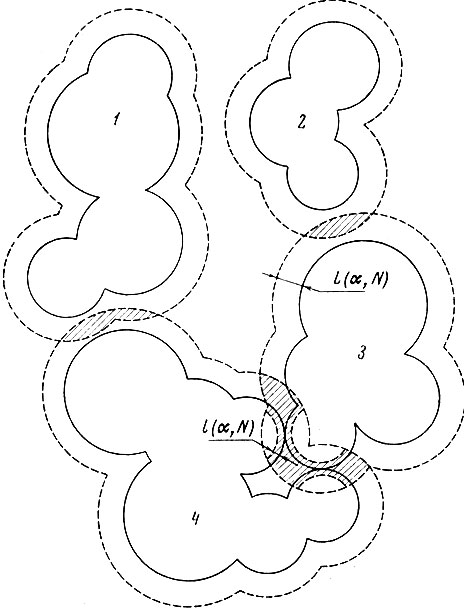
7.1. Коррекция решающего правила (заштрихованные области - области альтернативных ошибок)

Очевидно, что после такого расширения эталонных оболочек реализации всех образов не должны попадать вне расширенных оболочек с вероятностью не меньшей, чем α_L.

Если при этом доверительная вероятность α_L связана, с уровнем ошибок отказа β_L соотношением

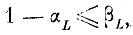
то доля ошибок отказа после первого шага коррекции на экзамене не может оказаться больше, чем α_L.

Расширенные эталонные оболочки могут в той или иной мере пересекаться. Это, естественно, приводит к увеличению ошибок альтернативного типа.

2. Второй шаг направлен на минимизацию областей альтернативных ошибок при сохранении заданного уровня β ошибок неправильного опознания.

После первого шага возможны три случая:

а) "Распухшие" эталонные оболочки не пересекаются (см. рис. 7.1; образы 1 и 2). Если при этом

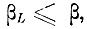
то нет необходимости во введении дополнительных областей альтернативных ошибок, так как относительная доля суммы ошибок отказа и ошибок неправильного опознания не может превысить заданной величины β. Такая ситуация может встретиться для далеких образов.

б) Пересекаются только расширенные оболочки образов (см. рис. 7.1; образы 2, 3 и образы 1, 4). Область пересечения принимается за область альтернативных ошибок (если β_L≤β).

в) "Распухшие" оболочки образов частично захватывают первоначальные эталонные оболочки, построенные по учебной выборке (см. рис. 7.1; образы 3 и 4). Такая ситуация характерна для "близких" образов.

В этом последнем случае производится минимизация области альтернативных ошибок. Для этого места "захвата" первоначальных оболочек сжимаются но всем направлениям в пространстве признаков на величину l(α_l, N) - максимально возможное проникновение реализаций в эталонные оболочки "чужих" образов с доверительной вероятностью α_l. Величина α_l назначается из условия

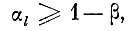
где β - требуемый уровень ошибок неправильного опознания. Если "сжатая" оболочка образа пересекается с "расширенными" оболочками каких-либо "чужих" образов (см. рис. 7.2), то эта область пересечения исключается из области альтернативных ошибок, полученной на первом шаге коррекции. Такое сокращение области альтернативных ошибок допустимо, так как из способа определения величины l(α_l, N) следует, что "чужие" реализации с вероятностью не могут проникать глубже, чем на д в эталонную оболочку рассматриваемого образа. Если же "сжатая" на величину l (α_l, N) эталонная оболочка образа не пересекается ни с одной из "расширенных" оболочек чужих образов, то за область альтернативных ошибок принимается, как и в пункте б, область пересечения расширенных на величину L (α_L, N) оболочек образов, даже если область пересечения захватывает первоначальные эталонные оболочки образов (см. рис. 7.3).

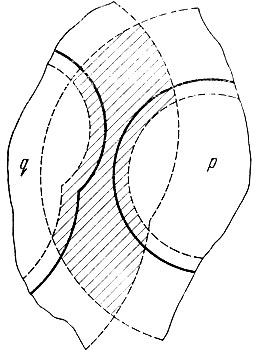
7.2. Формирование области альтернативных ошибок в случае, когда расширенные эталонные области образов 'захватывают' сжатые эталонные области чужих образов

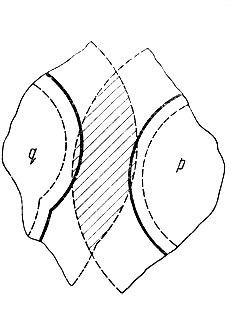
7.3. Формирование области альтернативных ошибок в случае, когда расширенные эталонные области не 'захватывают' сжатых эталонных областей 'чужих' образов

Минимум областей альтернативных ошибок при данном способе коррекции достигается, если экстремальные параметры L(α_L, N), l(α_l, N) оцениваются с одинаковыми доверительными вероятностями, т. е. α_L=α_l=α=1-β. (Доказательство этого факта см. в приложении 7.1.) Следовательно, уровень ошибок отказа в этом случае также не превышает величины β - требуемого уровня ошибок неправильного опознания.

Окончательно скорректированные эталонные оболочки представляют собой расширенные первоначальные оболочки образов за вычетом областей альтернативный ошибок.

В эти скорректированные оболочки с вероятностью а, в силу способа их изменения не могут попадать реализации чужих образов, поэтому относительная доля ошибок неправильного опознания на будущей большой экзаменационной выборке не может превышать

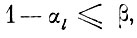
т. е. заданной величины.

Число эталонов после коррекции может несколько увеличиться по сравнению с исходным решающим правилом. Однако так как скорректированные эталонные оболочки образов и области альтернативных ошибок формируются только из "расширенных" и "сжатых" исходных эталонных оболочек, то число эталонов не может увеличиться более чем в два раза. Такое предельное увеличение может произойти лишь тогда, когда каждый "сжатый" эталон любого образа "захватывается" достаточно глубоко "расширенными" эталонами каких-либо чужих образов. В практических ситуациях, когда имеются и относительно "далекие", и относительно "близкие" друг другу образы, увеличение числа эталонов незначительно.

Описанная процедура статистической коррекции является непараметрической. Поэтому большая начальная неопределенность не позволяет оценить фактическую "степень заполнения" сформированных областей альтернативных ошибок - часть из них может оказаться просто пустой.

Следует также отметить, что обеспечиваемый после коррекции прогноз ошибок отказа и ошибок неправильного опознания является оценкой сверху, так как "предельное" расширение и сжатие первоначальных эталонных оболочек производятся по всем направлениям равномерно.

Таким образом, смысл коррекции решающего правила заключается, с одной стороны, в выделении в пространстве признаков таких взаимно не пересекающихся максимального размера областей различных образов, что с заданной вероятностью а в эти области не должны проникать реализации "чужих" образов, а с другой стороны, - в минимизации областей альтернативных ошибок.