§ 7.3. Процедура получения оценок L (αL, N) и l(αl, N) но конечной выборке

Для получения оценки L (α_L, N) - максимально возможного выброса реализации за эталонные оболочки образов

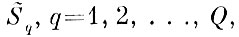
как уже указывалось в § 7.1., необходима независимая контрольная выборка. Процедура заключается в следующем.

Каждая реализация контрольной выборки

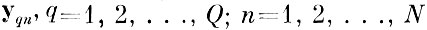
сопоставляется с некоторой величиной, численно равной минимальному расстоянию до границы эталонной оболочки S̃_q своего образа, а знак этой величины является индикатором попадания реализации внутрь или наружу эталонной области S_q, т. е. по контрольной выборке измеряются величины:

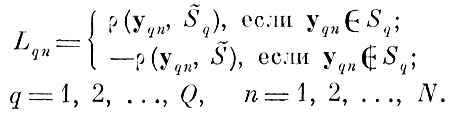
Полученная выборка {L_qn} объема QN подчиняется функции распределения "расстояний" реализаций до своих эталонных оболочек с учетом знака. Эту одномерную функцию распределения мы рассматриваем как исходную.

В силу одинаковости построения эталонных оболочек для всех образов, непрерывности и ограниченности распределений образов рассматриваемое распределение выбросов также непрерывно и ограничено слева некоторой отрицательной величиной L - максимально возможным выходом реализаций за свою эталонную оболочку. Эту величину и требуется оценить. Постулируя выполнение также условия "гладкости слева" [7.2], задача оценки L по выборке {L_qn} становится аналогичной задаче оценки меры не пересекаемости образов, детально описанной в главе III.

Для получения оценки l(α_l , N) максимально возможного проникновения реализаций в эталонные оболочки чужих образов необходимо рассмотреть в качестве исходного другое одномерное распределение, а именно, распределение "расстояний" между реализациями образов и ближайшей эталонной оболочкой "чужого" образа.

Чтобы получить выборку, принадлежащую этому распределению, каждая реализация контрольной выборки y_qn,

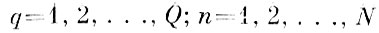
сопоставляется с некоторой

величиной, численно равной минимальному расстоянию до ближайшей чужой эталонной оболочки, а знак этой величины является, как и в предыдущем случае, индикатором попадания или непопадания этой реализации внутрь эталонной оболочки "чужого" образа, т. е. по контрольной выборке находятся величины

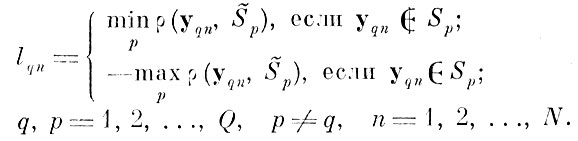
Постулируя, как и ранее, аналогичные ограничения на рассматриваемую функцию распределения, можно использовать алгоритм оценки меры непересекаемости образов для получения по выборке {l_qn} оценки l - максимального проникновения реализаций образов в эталонные области чужих образов.

Точечные оценки L̂ и l̂ покрываются доверительными интервалами, построение которых описано в главе III.

Нижние границы этих доверительных интервалов

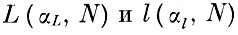
и используются при коррекции решающего правила.