Приложение 7. II. О сходимости метода эталонов к безошибочному решающему правилу

Для ε-непересекающихся образов, как показано в главе II, существует множество решающих правил, построенных из конечного числа эталонов и обладающих нулевой ошибкой на бесконечной выборке.

Эталонные оболочки строятся и корректируются по конечным выборкам. Поэтому весьма важными являются вопросы сходимости алгоритмов метода эталонов вместе с процедурой коррекции к безошибочному решающему правилу при увеличении объема учебной выборки.

Ясно, что сходимость эталонных оболочек к не пересекающимся покрытиям образов может иметь место лишь при определенных ограничениях на способы построения решающего правила и коррекции, а также на статистику предъявляемых при обучении реализаций различных образов [7.5].

Докажем предварительно леммы о сходимости некоторого идеализированного способа построения эталонных оболочек (покрытий) образов к безошибочному решающему правилу. Результаты этих лемм будут использованы в дальнейшем.

Лемма 1. Пусть

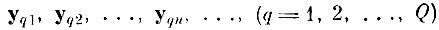
бесконечная последовательность независимых случайных точек (реализаций q-ro образа) в I-мерном эвклидовом пространстве Y с абсолютно непрерывной вероятностной мерой F_q (по мере Лебега) такой, что плотность

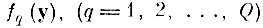
отлична от нуля в каждой точке некоторой ограниченной области

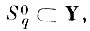
за исключением, быть может, множества меры нуль.

Пусть также

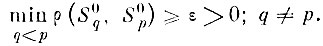
Образуем последовательность областей

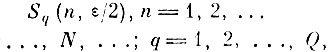
состоящих из объединения шаров s_qn (ε/2) = {y ∈ Y : ρ (y_qn, y) ≤ ε/2} с центрами в точках последовательности y_qn, радиуса

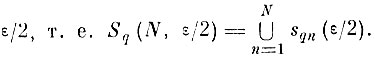
Тогда для любого наперед заданного δ > 0 можно подобрать такое конечное N*, что с вероятностью Р ≥ 1 - δ покрытие S_q (N*, ε/2) будет включать в себя все точки "своего" образа

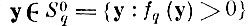
и не будет включать ни одной точки "чужих" образов

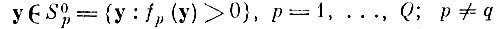
или

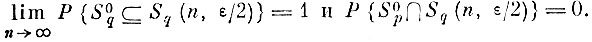
Доказательство. Из способа построения покрытий

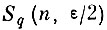
для любого n следует, что вероятность "захвата" чужих точек

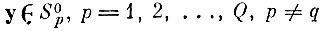
равна нулю, т. е.

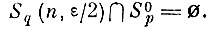
Разобьем область

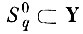
на некоторое число М не пересекающихся (не нулевой меры) подмножеств

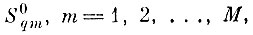
такое, что вероятность попадания каждой точки

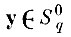
в любое из них одинакова и равна 1 /М, а диаметр каждого из подмножеств не превышает ε/2, т.е.

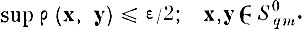
Это можно сделать в силу ограничений на F_q. Вероятность того, что отрезок последовательности случайных независимых точек

длиной N ≥ М заполнит все ячейки

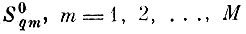
(т. е. в каждую из ячеек попадет хотя бы одна точка), очевидно, равна вероятности того, что при случайном размещении N одинаковых шаров по М ящикам не окажется ни одного пустого ящика. Эта вероятность равна [7.3] и

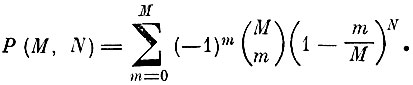(7.II.1)

С увеличением N для любого конечного М эта вероятность стремится к единице.

А так как каждый шар

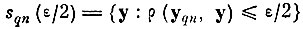
полностью покрывает какую-либо ячейку S⁰_qm, в которую попила точка y_qn, то область

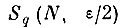
с вероятностью, не меньшей, чем Р (М, N), покроет область S⁰_q, не захватывая при этом ни одной "чужой" точки

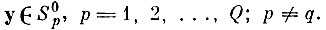
Следовательно, для любого δ>0 можно подобрать такое

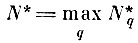
(7. II. 1), что: я

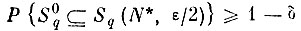
или

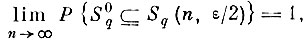(7.II.2)

т. е. последовательность областей

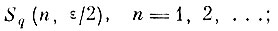
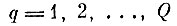
сходится по вероятности к не пересекающимся покрытиям образов. Доказательство закончено.

На самом деле имеет место более сильная сходимость последовательности случайных покрытий

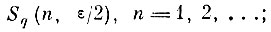
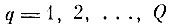
к безошибочному решающему правилу, а именно, что для каждой в отдельности бесконечной цепочки процесса

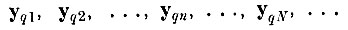
последовательность областей

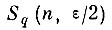
сходится к не пересекающимся покрытиям образов, т. е. имеет место сходимость с вероятностью единица.

Лемма 2. В условиях леммы 1 последовательность случайных областей

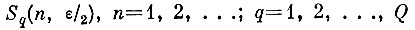
сходится почти наверное (с вероятностью единица) к не пересекающимся покрытиям образов.

Доказательство. Рассмотрим последовательность событий А_n, n = 1, 2, . . ., состоящих в том, что области

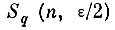
не покрывают S⁰_q или, что эквивалентно, при размещении n шаров по М ящикам остается хотя бы один пустой ящик.

Очевидно, что каждое из этих событий зависит только от конечного числа испытаний.

Для произвольной фиксированной бесконечной цепочки

рассмотрим теперь событие U_r, состоящее в том, что результаты бесконечной последовательности испытаний благоприятствуют более чем r событиям А_n.

Вероятность осуществления события А_n, учитывая (7.II.1), равна

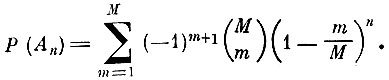(7.II.3)

Тогда в силу того, что ряд

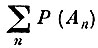
сходится^*, на основании леммы Бореля-Каителли [7. 3] с вероятностью единица, произойдет только конечное число событий А_n. Более точно: для любого δ>0 найдется целое число r, такое, что, каково бы ни было n, вероятность того, что в результате п испытаний произойдет одно или больше событий

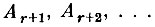
меньше чем 8, т. е.

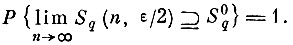(7.II.4)

^* (Сходимость ряда

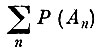
легко установить, например, по интегральному признаку Каши [7.4])

Доказательство закончено.

В действительности построение эталонной области в виде ε-сети является чрезмерно трудоемкой процедурой, если границы между образами сложны, а сами образы близки друг к другу.

Стремление осуществить покрытие образа как можно меньшим числом эталонов приводит к тому, что в каждой точке обучающей выборки строится эталон как можно большего радиуса при условии непопадания в него реализаций "чужих" образов (см. главу VI). Например, в каждой точке учебной выборки строится эталон радиусом, равным половине расстояния до ближайшей реализации "чужого" образа. Кроме того, построенное покрытие минимизируется.

Сходимость детерминированного метода эталонов к безошибочному решающему правилу устанавливает

Теорема 1. Пусть

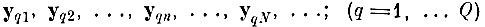
бесконечная последовательность случайных независимых реализаций различных образов в I-мерном эвклидовом пространстве в условиях леммы 1. Образуем для некоторого N области

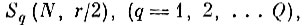
состоящие из объединения шаров

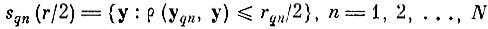
с центрами в точках случайной последовательности {y_qn} радиуса

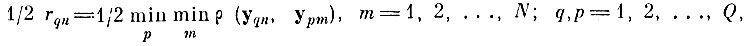
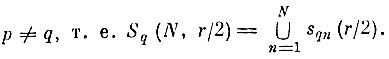(7.II.5)

Тогда последовательность областей

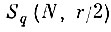
такова, что

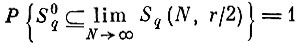
и

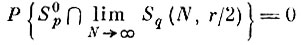(7.II.6)

для всех

т. e. последовательность областей

сходится с вероятностью единица к не пересекающимся покрытиям образов.

Доказательство. Докажем сначала, что с вероятностью единица последовательность областей

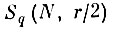
"захватывает" все "свои" точки

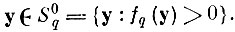
Доказательство сводится к замечанию о том, что для любого N и любой фиксированной бесконечной реализации процесса

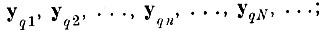
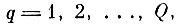
для шаров

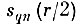
выполняется условие

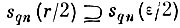
(определение множества

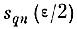
дано в лемме 1), так как, очевидно, всегда

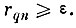
Следовательно, и

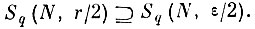(7.II.7)

Но тогда

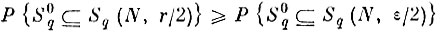
для любого N и каждого q.

Переходя к пределу и используя результат леммы 2, получим, что

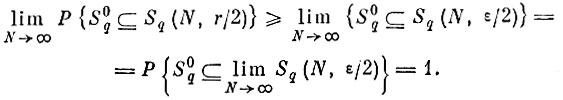
Но так как (7.II.7) верно для любого N и любой фиксированной бесконечной реализации процесса {y_qn}, то, очевидно, верно и

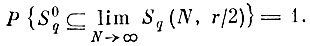
Первая часть доказана.

Докажем теперь, что последовательность областей сходится с вероятностью единица к не пересекающимся покрытиям образов, т. е. эталонные оболочки образов не будут "захватывать" (в смысле указанном в лемме 2) реализаций "чужих" образов.

Из леммы 2 следует, что ε-сеть с вероятностью единица покрывает область

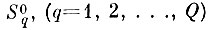
каждого образа при N→∞. Следовательно, для любой реализации y_qn какого-либо q-то образа ближайшее расстояние до реализаций "чужих" образов из любой фиксированной бесконечной последовательности

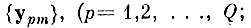
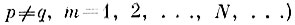
с вероятностью единица при N→∞ окажется меньше или равно

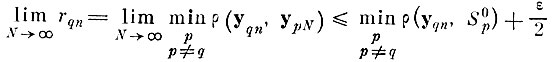
или

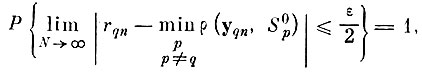
где

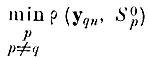
расстояние до ближайшего "чужого" образа от точки y_qn. Но так как всегда

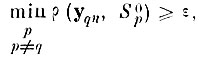
то в том же смысле

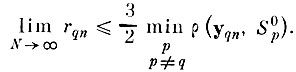
Следовательно, шар

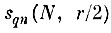
для любой точки y_qn не будет "захватывать" с вероятностью единица при N→∞ областей

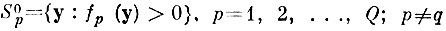
"чужих" образов, т. е.

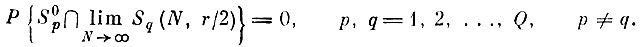
Теорема доказана.

Сделаем теперь несколько замечаний о скорости сходимости эталонных областей

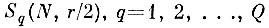
к не пересекающимся покрытиям образов.

Как видно из (7.II.1) и (7.II.3), быстрота сходимости существенно определяется отношением N/М, где число М (число ячеек одинаковой меры, диаметр которых не превосходит ε/2) в свою очередь зависит от f_q и ε. Для больших отношений N/M можно дать асимптотическое выражение для (7.1.1)

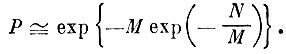(7.II.8)

Качественно зависимость N_q от величины ε и вида f_q(y) легко усмотреть из рис. 7. 8. На рис. 7.8, а представлены области двух "далеких" образов. Очевидно, что как бы ни были сложны их распределения f_q(y) и f_p(y) в силу того, что расстояние между ними ε значительно превосходит собственные диаметры образов, достаточно лишь по одному "показу", чтобы построить безошибочное решающее правило.

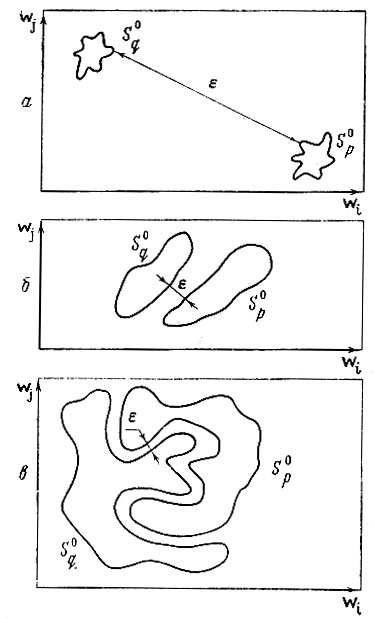
7.8. Оболочки образов q и р различной сложности

На рис. 7.8, б изображены две значительно менее сложные по конфигурации области образов, однако соотношение между минимальным расстоянием между ними ? и их диаметрами несколько хуже. В этом случае потребуется большее число показов, чтобы сформировать безошибочное решающее правило, особенно если статистика показов такова, что отдает предпочтение неблагоприятным для разделения точкам.

И, наконец, на рис. 7.8, в изображен случай, когда только почти полное восстановление распределений образов позволит построить приемлемое решающее правило.

Не менее важным при построении решающего правила является формулировка правила остановки процесса обучения, обеспечивающая заданную надежность опознания на экзамене [7.5]. При неизвестных распределениях образов воспользоваться результатами

Предыдущих теорем нельзя, так как невозможно оценить число

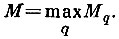
Правило остановки должно быть непараметрическим и вырабатывается в процессе обучения в соответствии с заданными требованиями к уровням ошибок.

С этой целью можно использовать описанную процедуру статистической коррекции решающего правила многократно и наблюдать за изменением прогноза величин ошибок (которые в результате коррекции становятся контролируемыми) после каждого исправления решающего правила. Если прогноз ошибок после очередного исправления удовлетворяет заданным требованиям, то процесс обучения можно прекратить.

Многократная коррекция осуществляется следующим образом. Если к n-му шагу коррекции области альтернативных ошибок остались еще достаточно велики, то контрольная выборка, использовавшаяся для n-й коррекции, смешивается с учебной выборкой, накопленной к n-му шагу. По увеличенной выборке решающее правило методом эталонов строится заново. В новые эталонные области "бросается" следующая (n+1)-я контрольная выборка, и оболочки вновь корректируются и т. д.

Напомним, что на любом шаге коррекции уровень ошибок неправильного опознания и ошибок отказа поддерживается одним и тем же. Изменяется лишь величина альтернативных ошибок.

Сходимость с вероятностью единица процедуры многократной коррекции вытекает из сходимости метода эталонов. Более того, можно показать, что за конечное число исправлений можно достичь отсутствия альтернативных ошибок при заданном уровне ошибок неправильного опознания и ошибок отказа. Другими словами, за конечное число исправлений (возможно, свое для каждой конкретной последовательности

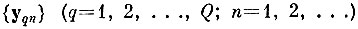
обучающей выборки) можно построить не пересекающиеся покрытия образов.

В самом деле, с увеличением объема учебной выборки формируемые эталонные оболочки все лучше покрывают неизвестные области образов

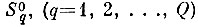
и все лучше аппроксимируют пограничные области между образами. Точные границы распределений образов могут быть получены лишь на бесконечной выборке, но границы, размытые на величину ε/2 с заданной вероятностью Р, достигаются на некотором конечном

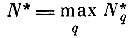
(см. леммы 1 и 2). Это и будет величина такого объема выборки, что оценка максимального выброса реализаций за свои эталонные оболочки L(α, N) с заданной вероятностью α = Р не превзойдет ε/2.

Таким образом, расширенные эталонные оболочки не пересекутся и обеспечивается требуемое качество решающего правила при нулевой величине альтернативных ошибок. Это и будет тот момент, когда можно прекратить процесс обучения.

Заметим, что при многократной коррекции зависимость минимума альтернативных ошибок от способов построения исходных эталонных оболочек ослабевает, происходит своего рода забывание и условный минимум превращается в безусловный.