Приложение 7. I. Формальное описание процедуры коррекций решающего правила

Пусть

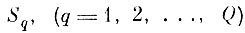
исходные эталонные области

образов в пространстве признаков Y, построенные по учебной выборке из условии ее безошибочного опознания.

Обозначим через

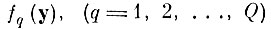
неизвестные нам многомерные распределения образов в Y.

Тогда вероятность ошибки неправильного опознания для исходного решающего правила можно записать в виде

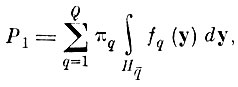(7.I.1)

где π_q - вероятность появления q-го образа, которую в некоторых задачах можно принять равной 1/Q; Q - количество образов; H_q̄ - область в Y, определяемая соотношением

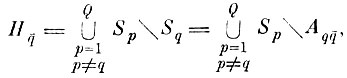
где A_qq̄ - область альтернативных ошибок q-го образа

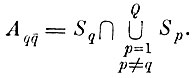(7.I.2)

Заметим, что если алгоритм формировании исходных эталонных областей

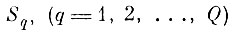
не допускает их пересечения, т. е.

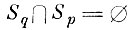
для всех

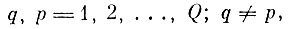
то области альтернативных ошибок до процедуры коррекции отсутствуют. В этом случае в (7.1.1)

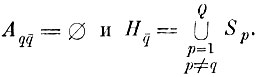
Вероятность ошибок тина отказа имеет вид

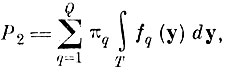(7.I.3)

где Т - область отказа, определяется соотношением

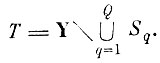
И, наконец, вероятность альтернативных ошибок для исходного решающего правила можно записать в виде

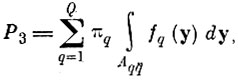(7.I.4)

где А_qq̄ - область альтернативных ошибок q-го образа со всеми остальными (определена в (7. I. 2)].

В частности, как уже указывалось, если

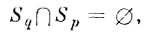
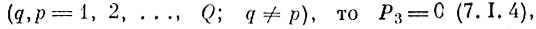
так как при этом автоматически

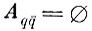
для всех q = 1, 2, .... Q.

Отметим, что величины всех трех видов ошибок Р₁, Р₂ и Р₃ при детерминированном способе построения решающего правила остаются неизвестными для любого конечного объема обучающей выборки, так как получить оценки интегралов (7. I. 1), (7.1.3) и (7. I. 4) при неизвестных распределениях образов не представляется возможным.

Однако с помощью некоторых одномерных предельных статистических характеристик можно изменять конфигурацию областей S_q, A_qq̄ и Т так, что величины ошибок (7.1.1), (7.1.3) после изменения становятся контролируемыми.

Это обстоятельство и позволяет осуществить непараметрическую коррекцию решающего правила с целенаправленным изменением соотношения и величии рассмотренных видов ошибок.

Пусть L (α_L, N) и l (α_l, N) - оценки максимально возможного выброса реализаций за "свои" эталонные оболочки образов с доверительной вероятностью α_L и максимально возможного проникновения реализаций в глубь эталонных оболочек "чужих" образов с доверительной вероятностью α_l, соответственно.

Пусть также задан требуемый уровень р ошибок неправильного опознания.

В этих условиях требуется изменить конфигурации исходных эталонных областей

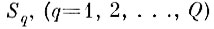
так, чтобы минимизировать величины ошибок отказа и альтернативных ошибок при сохранении уровня ошибок неправильного опознания не выше заданного.

Процедура коррекции решающего правила производится в два шага.

1. Увеличим все исходные эталонные области образов

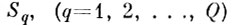
по всем направлениям в Y на величину L (α_L, N). Тогда- для расширенных областей, обозначим их S_q(L), вероятность того, что "своя" реализация выйдет за цх границы S̃_q(L), не превосходит величины

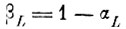
силу способа определения оценки экстремального параметра L (α_L, N) - как максимально возможного выброса реализаций за "свои" исходные эталонные оболочки с доверительной вероятностью α_L.

Следовательно, вероятность ошибки отказа для новых расширенных эталонных областей

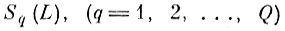
не может превзойти величины β_L, т. е.

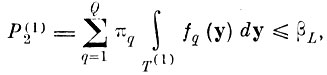(7.I.5)

где T⁽¹⁾ - область отказа после первого шага, которая определяется соотношением

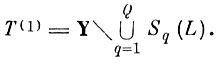(7.I.6)

Расширенные эталонные области

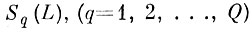
могут в той или иной мере пересекаться в зависимости от взаимной удаленности образов друг от друга и способа построения исходных эталонных областей S_q.

Область пересечения областей

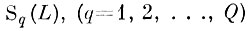
образует область альтернативных ошибок, которая после первого шага имеет вид

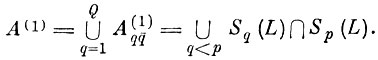(7.I.7)

Определим эталонные области образов после первого шага соотношением

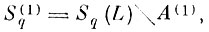
т. e. из расширенных эталонных областей S_q(L) удалим все области альтернативных ошибок (7. I. 7).

Тогда вероятность ошибок неправильного опознания для областей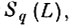
, (q = 1, 2,....,Q) не может превышать величины

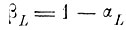
Это также следует из способа определения оценки экстремального параметра L(α_L, N).

Таким образом, с помощью оценки параметра L (α_L, N) для эталонных областей образов мы получили непараметрические Оценки вероятностей ошибок отказа (7.1.5) и ошибок неправильного опознания (7. I. 8).

Очевидно, что эти оценки являются оценками сверху в силу равномерного по всем направлениям в Y предельного расширения исходных эталонных областей S_q.

Если потребовать, чтобы доверительная вероятность α_L максимально возможного выброса реализаций за "свои" исходные эталонные оболочки L (α_L, N) была такова, что

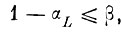
то уровень ошибок неправильного опознания не превзойдет заданного. То же верно и для ошибок типа отказа.

2. Второй шаг коррекции решающего правила направлен на минимизацию альтернативных ошибок при сохранении заданного уровня β ошибок неправильного опознания.

После первого шага вероятность альтернативных ошибок равна

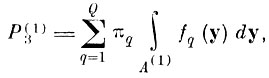(7.I.9)

где А⁽¹⁾ - область пересечения расширенных областей S_q(L), (q = 1, 2, . . ., Q) определена в (7.1.7).

Так как распределения образов f_q(у) неизвестны, то непараметрическая минимизация величины альтернативных ошибок P⁽¹⁾₃ (7. 1.9) может быть осуществлена лишь за счет равномерного или локально равномерного по всем направлениям в Y сжатия области пересечения А⁽¹⁾. При этом сжатие области альтернативных ошибок А⁽¹⁾ не должно увеличивать заданный уровень β ошибок неправильного опознания, который уже обеспечивается после первого шага коррекции.

Для минимизации альтернативных ошибок используется второй экстремальный параметр l (α_l, N) - максимально возможное проникновение реализаций в глубь исходных эталонных областей "чужих" образов с доверительной вероятностью α_l.

Сожмем исходные эталонные области

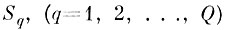
по всем направлениям в Y на величину N). Обозначим "сжатые" области через S_q(l), (q = 1, 2, . . ., Q). Найдем пересечение сжатых областей S_q(l) с расширенными S_q(L)

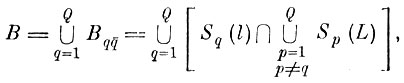(7.I.10)

где

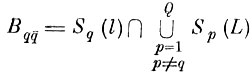
область пересечения q-и сжатой эталонной области со всеми остальными расширенными областями

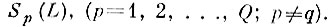
Из определения величины l(α_l, N) следует, что реализации различных образов с вероятностью α_l не могут проникать глубже, чем на l(α_l, N). в "чужие" эталонные оболочки. Если при этом потребовать, чтобы доверительная вероятность а/ была связана с заданным уровнем β ошибок неправильного опознания соотношением 1 - α_l ≤ β, то очевидно, что, не увеличивая вероятность ошибок неправильного опознания, можно каждую из областей В объединить с эталонными областями образов, сформированных после первого шага коррекции. Или, что эквивалентно, уменьшить область альтернативных ошибок А⁽¹⁾ до величины

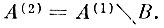(7.I.11)

Размеры областей A⁽¹⁾ и В при фиксированных исходных эталонных областях образов S_q, q = 1, 2, . . ., Q зависят от действительных величин L(α_L, N) и l(α_l, N) Последние в свою очередь

зависят от доверительных вероятностей α_L и α_l как выборочные оценки, полученные по контрольной выборке конечного объема N.

Покажем, что минимальные размеры области альтернативных ошибок A⁽²⁾ после второго шага коррекции достигаются, если

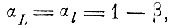
при условии, что уровень ошибок неправильного опознания не превосходит заданной величины β.

В самом деле, размеры области В(α_L, α_l) могут только увеличиваться, если уменьшается (при фиксированном α_L), т. е.

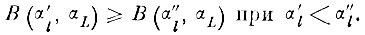
Но величина α_l не может быть выбрана меньше, чем α_l = 1 - β, так как в противном случае при объединении областей

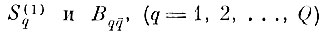
может возрасти уровень ошибок неправильного опознания.

Поэтому максимальные размеры области пересечения в сжатых и расширенных эталонных оболочках при некотором фиксированном α_L достигаются при α_l = 1 - β.

С другой стороны, размеры области A⁽¹⁾ альтернативных ошибок после первого шага коррекции могут только возрасти при увеличении

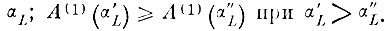
Но доверительная вероятность α_L также не может быть выбрана меньше, чем α_L = 1 - β, как в противном случае может увеличиться уровень ошибок неправильного опознания в силу того, что вероятность выхода реализаций за эталоне оболочки "своих" образов возрастает.

Другими словами, если

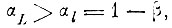
то сокращение области альтернативных ошибок не максимально. Если же

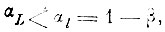
то величина альтернативных ошибок может только уменьшаться, но при этом может увеличиваться вероятность ошибок неправильного опознания.

Следовательно, максимальное сжатие области происходит, если

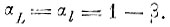
При этом область альтернативных ошибок определяется как

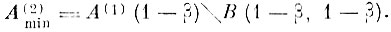(7.I.12)

Абсолютная величина альтернативных ошибок в области

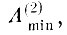
естественно, остается неизвестной

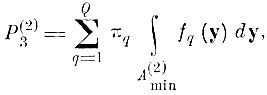
так как невозможно оценить фактическую "степень заполнения" области

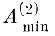
при неизвестных распределениях

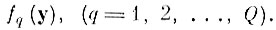
Таким образом, после двух шагов окончательно сформированные эталонные области образов, обозначим их

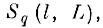
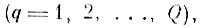
будут иметь вид

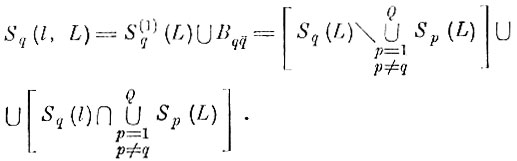(7.I.13)

В эти скорректированные эталонные области с вероятностью нс меньшей, чем α = 1 - β, не должны попадать реализации "чужих" образов.

Этим обеспечивается требуемый уровень β ошибок неправильного опознания. Уровень ошибок отказа также не превышает величины β.

Абсолютная величина условного минимума альтернативных ошибок, как уже указывалось в § 7.2, существенным образом зависит от того, как были построены исходные эталонные области образов

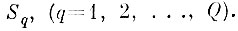
Очевидно, что чем меньше смещение эталонных областей S_q (которые строятся по учебной выборке) относительно неизвестных истинных областей образов

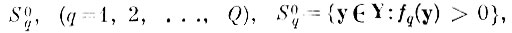
тем лучше будут результаты коррекции, тем меньше будет область альтернативных ошибок А⁽²⁾.

Фактически процедура коррекции как раз и направлена на ликвидацию смещения эталонных областей S_q относительно истинных областей образов S⁰_q с помощью оценок предельных параметров

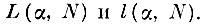
При этом параметр L - максимально возможный выброс реализации за "свою" эталонную область - рассматривается как некоторая мера "недостаточности" областей S_q относительно областей S⁰_q

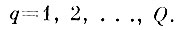
Параметр l - максимально возможное проникновение реализаций в глубь эталонных областей "чужих" образов - рассматривается как некоторая мера "избыточности" эталонных областей S_q относительно истинных областей S⁰_q.

Результаты однократной коррекции наряду с прогнозом поведения опознающего автомата па экзамене позволяют ответить па вопрос о том, хорошо ли были построены исходные покрытия образов по учебной выборке.