§ 8.2.3. Применение аппроксимационного критерия

Алгоритм нахождения системы линейных признаков по аппроксимационному критерию (см. § 4.2) является наиболее простым. Применение этого критерия для понижения размерности описания может дать положительный эффект, если параметры исходного описания сильно коррелированы (наличие тесной коррелированности параметров исходного описания является косвенным подтверждением

того, что матрица ковариации

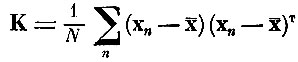
близка к вырожденной и все реализации учебной выборки лежат в подпространстве меньшей размерности).

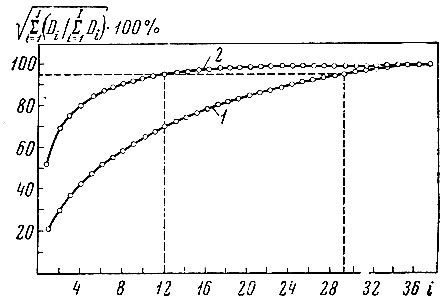
8.4. Зависимость среднеквадратичного расстояния между реализациями и общим центром тяжести от числа используемых параметров в пространстве (1) исходного описания и (2) признаков, найденных по аппроксимационному критерию

Это свойство аппроксимационного критерия подтверждает и эксперимент.

Из таблицы 8.1 видно, что в данном исходном описании аппроксимационный критерий может дать понижение размерности при достаточно точном в среднем описании реализаций образов. На рис. 8.4 представлены зависимости среднеквадратичного расстояния между реализациями и общим центром тяжести в процентах от числа используемых параметров исходного описания и признаков, найденных по аппроксимационному критерию. Для приближения со среднеквадратичной ошибкой аппроксимации, равной 5%, от среднеквадратичного расстояния в полном пространстве требуется подпространство из 12 признаков, представляющих собой линейные комбинации из 37 параметров исходного описания. В исходном пространстве такая же ошибка будет иметь место при сохранении 29 из 37 параметров.

Вместе с тем аппроксимационный критерий не вполне адекватен задаче распознавания образов, так как в нем не содержится никаких требований, направленных на сохранение в пространстве признаков свойств разделимости образов. Этот недостаток очевиден и все же он будет проиллюстрирован при обсуждении свойств взвешенного дискриминантного критерия в 8.2.5.